
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рубежный контроль 2 (контроль по модулю №2)Содержание книги
Поиск на нашем сайте
1. Производная функции комплексного переменного. Вывести необходимые условия дифференцируемости функции комплексного переменного. 2. Найти круг сходимости степенного ряда и исследовать поведение ряда в четырёх точках границы этого круга: самой верхней, самой нижней, самой левой, самой правой: 3. Вычислить с помощью интегральной формулы Коши или её следствия (формулы n-ой производной) интеграл 4. Найти все разложения функции Модуль 3. Теория вычетов и операционное исчисление Домашнее задание № 3 Часть 1 Задача 1 Найти все особые точки заданной функции
Задача 2 Вычислить интеграл Часть 2 Задача 1 Пользуясь теоремами интегрирования изображения и интегрирования оригинала, найти изображения заданных функций; найденный результат проверить для первой из заданных функций по первой теореме разложения, развёртывая в ряды как оригинал, так и полученное изображение: Задача 2 Пользуясь теоремой свёртывания, найти оригинал первой из заданных функций, для отыскивания оригиналов в остальных использовать полученный результат, либо теорему дифференцирования, либо теорему интегрирования оригинала. Ответ к последнему из заданных примеров проверить, либо находя по полученному оригиналу его изображение, либо находя сам оригинал иным способом – по 2-й или по обобщённой (3-й) теоремам разложения: Задача 3 При помощи обобщённой (третьей) теоремы разложения найти оригиналы заданных функций; ответ проверить, пользуясь второй теоремой разложения:
Задача 4 Найти изображения заданных ниже при помощи чертежа периодической функции (на чертеже изображён первый период и пунктиром намечено начало второго) В данном примере использованы параболы 2-го порядка с вертикальной осью. 
Рубежный контроль №3 (контроль по модулю №3)
1. Прямое и обратное преобразование Лапласа. Доказать теорему о существовании изображения. 2. Вычислить интеграл от функции комплексного переменного, классифицировав все особые точки функции, включая бесконечно удаленную точку 3. Найти изображение по заданному оригиналу и оригинал по заданному изображению 4. Решить дифференциальное уравнение при заданных начальных условиях, проверить полученное решение:
Вопросы для подготовки к рубежным контролям и экзамену
|
||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 381; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.50.71 (0.007 с.) |

 .
. .
. по степеням
по степеням  . Указать область пригодности (сходимости) каждого из разложений.
. Указать область пригодности (сходимости) каждого из разложений. ; определить их характер и найти вычеты в них. Установить, чем является для данной функции бесконечно удалённая точка и найти вычеты в ней.
; определить их характер и найти вычеты в них. Установить, чем является для данной функции бесконечно удалённая точка и найти вычеты в ней. при помощи теории вычетов, по контуру
при помощи теории вычетов, по контуру  :
:  .
.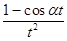 ,
,  .
. ,
,  ,
,  .
. .
. .
. .
. .
.


