
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторные и матричные операторыСодержание книги
Поиск на нашем сайте
Введем обозначения: V1, V2 – векторы, M – матрица, Z – скаляр. ПустьV1:= V1 + V2 = V1 - V2 = -V2 = V1 – Z = -М = Z*V1 = Z*M = V1*V2 = 32 – операция скалярного умножения двух векторов V1 и V2. М*V2 = М*М1 = V1/Z = M/Z = M^3 = M-1 = |V1 = 3.762 – операция вычисление модуля вектора |V1|. |M = 0 – операция вычисления определителя матрицы М. V1 Ctrl! = (1, 2, 3) – операция транспонирования вектора V1. M Ctrl! = V1 Ctrl * V2 = V1 Ctrl - = M Ctrl - = M Ctrl ^ 2 = V1 [ 2 = 3 – операция выделения 2 – го элемента вектора V1. M [1,1 = 5 – операция выделения элемента (1,1) матрицы М. [ открывающаяся скобка используется для ввода индекса элемента массива или вектора. . точка используется для ввода индекса скалярной переменной, причем синий уголок курсора ввода должен охватывать все имя переменной, а не только область ввода. Символьные вычисления. Команды, относящиеся к работе символьного процессора, содержатся в меню Symbolics (Символика). Для выполнения символьных операций процессору необходимо указать, над каким выражением они должны проводиться, т. е. надо выделить это выражение. Для ряда операций необходимо указать переменную, относительно которой выполняется символьная операция, при этом выражение не выделяется. Символьные вычисления выполняются в командном режиме, если реализуются команды меню Символика. Символьные вычисления могут проводиться с применением символьного оператора →.
Символьные вычисления в командном режиме выполняются только над явными выражениями (присутствие функций пользователя недопустимо). Результат вычислений может выводиться ниже исходного выражения, справа от него и вместо него. Способ вывода задается командой Evaluate Style (Стиль вычислений) меню Символика.
|
|||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.110.140 (0.009 с.) |

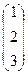 , V2:=
, V2:=  , M:=
, M:=  , M1:=
, M1:= 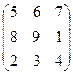 , Z:= 5.
, Z:= 5.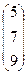 – операция сложения векторов V1 и V2.
– операция сложения векторов V1 и V2. - операция вычитание вектора V2 из вектора V1.
- операция вычитание вектора V2 из вектора V1. – операция смена знаков у элементов вектора V2.
– операция смена знаков у элементов вектора V2.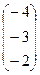 – операция вычитания скаляра Z из всех элементов вектора V1.
– операция вычитания скаляра Z из всех элементов вектора V1. - операция смены знаков у элементов матрицы М.
- операция смены знаков у элементов матрицы М. или V1*Z =
или V1*Z =  или M*Z =
или M*Z =  - операция скалярного умножения матрицы М на вектор V2.
- операция скалярного умножения матрицы М на вектор V2. – операция скалярного умножения двух матрицы М1 и М2.
– операция скалярного умножения двух матрицы М1 и М2. – операция деления всех элементов вектора V1 на скаляр Z.
– операция деления всех элементов вектора V1 на скаляр Z. – операция деления матрицы М на скаляр Z.
– операция деления матрицы М на скаляр Z. – операция возведение матрицы М в степень 3.
– операция возведение матрицы М в степень 3. – операция обращения матрицы М, т.е. нахождение обратной матрица.
– операция обращения матрицы М, т.е. нахождение обратной матрица. – операция транспонирования матрицы М.
– операция транспонирования матрицы М.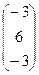 = – операция векторного умножения двух векторов V1 и V2.
= – операция векторного умножения двух векторов V1 и V2. – операция выделения 2 – го столбца матрицы М.
– операция выделения 2 – го столбца матрицы М.


