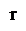Операции обновления отношений

В зависимости от изменений, происходящих на объекте реального мира в предметной области, происходит изменение состояния отношений в БД. Для реализации этих изменений используются операции обновления отношений.

Замечание: Приведенные далее имена операций ADD, DEL, CH не соответствуют именам в реальных СУБД. а приведены только для обозначения операций.

Добавление ADD новых кортежей в отношение

ADD (r; A₁ = d₁,..., A_K = d_K) - если порядок атрибутов в отношении может быть изменен.

ADD (r; d₁,..., d_K) - если порядок атрибутов не меняется.

Пример: r - группа датчиков

ADD (группа_датчиков; номер=100, назначение = измерение температур, тип = t - резисторный, подсистема = контроль аварийной ситуации)

 

При выполнении добавления возможно возникновение следующих ситуаций:

1) добавляемый кортеж не соответствует схеме указанного отношения (то есть имеются ошибки в атрибутах);

2) некоторые значения в кортеже не принадлежат соответствующим им доменам;

3) описанный кортеж совпадает (по ключу) с кортежем, уже имеющемся в отношении.

В этом случае операция ADD оставляет отношение без изменения и выдает признак ошибки.

 

Удаление DEL кортежа из отношения

DEL (r; A₁ = d₁,..., A_K = d_K) - если порядок атрибутов в отношении может быть изменен.

DEL (r; d₁,..., d_K) - если порядок атрибутов не меняется.

Если в отношении указан ключ К=(В₁,..., В_m), то удаление может выполняться только с указанием атрибутов ключа:

DEL(r; В₁ = С₁,..., В_m = C_m).

Удаление выполняется успешно всегда, если удаляемый кортеж идентифицирован в отношении. Таким образом, в результате выполнения операции удаления отношение может оказаться пустым. Пустое отношение допускается в БД.

Изменение части кортежа CH

Если в отношении r со схемой R [A₁,..., A_K] изменяется атрибут кортежа t { С₁,..., С_р }, то это выполняется с помощью оператора

СН (r; A₁ = d₁,..., A_K = d_K; С₁ = С₁,..., С_р = C_р)

Если К =(В₁,..., В_m) - ключ отношения, то

СН (r; В₁ = d₁,..., B_m = d_m; С₁ = С₁,..., С_р = C_р)

Операция СН может быть выполнена помощью последовательности операций удаления и добавления. Все ошибочные ситуации, связанные с этими операциями, присущи и операции изменения части кортежа.

Другие операции над отношениями

Кроме операторов реляционной алгебры используют операторы, играющие существенную роль с практической точки зрения.

Оператор расщепления

r(R), b (t) - предикат на кортеже t, t Î r

· Тогда расщеплением r по b (t) будет

SPLIT_b (r) = (S, S¢) таких, что

S ={ t Î r, b (t) = 1}

S¢= { t Î r, b (t) = 0}, S = r - S¢.

На предикат b (t) не накладывается никаких ограничений, за исключением одного, заключающегося в том, что b (t) зависит только от одного кортежа и не зависит от состояния отношения r(R). Например, предикат b (t) не должен зависеть от количества кортежей в отношении.

 

 

b (t) =(t (Тип_дат = T1) È t (Тип_дат = T4) SPLITb (r) = (S, S¢)

Пример:

	Тип Дат Имя пар-ра T1 P1 T1 P2 T2 P2 T2 P3 T3 P2 T4 P2 T4 P4
		S¢
		S
		Тип Дат Имя пар-ра T1 P1 T1 P2 T4 P2 T4 P4		Тип Дат Имя пар-ра T2 P2 T2 P3 T3 P2

 

Оператор “фактор”

В качестве аргумента оператора берется отношение r, а результатом являются два отношения.

FACTOR (r) = (S, L)

При выполнении операции “фактор” в исходном отношении выделяется некоторое количество атрибутов и соответствующие им столбцы отделяются от исходного отношения. Задается новый атрибут, который добавляется к схеме исходного отношения. Выделенные атрибуты вместе с новым атрибутом составляют схему результирующего отношения L. Добавленный атрибут является ключевым в отношении L.

r

L

S

Пример:

	Шифр Дат Тип Дат Имя п/сист А1 T1 P1 А2 T1 P2 А3 T2 P2 А4 T1 P1 А5 T2 P1 А6 T2 P2 А7 T1 P1		Шифр Дат Метка А1   А2   А3   А4   А5   А6   А7
			Тип Дат Имя п/сист Метка T1 P1   T1 P2   T2 P2   T2 P1

 

 

Функциональные зависимости

При одном и том же наборе атрибутов, описывающих предметную область может быть предложено множество различных вариантов группировки этих атрибутов в отношения, то есть множество различных вариантов построения логической схемы БД.

Удачность проекта в значительной степени зависит от того, насколько полно в нем были учтены естественные связи между данными, определяемые семантикой предметной области.

Пример:

Пусть имеется отношение “Датчик” (шифр_датчика, местоположение, параметр).

Использование такого отношения порождает ряд проблем:

1) Избыточность данных. Информация о местоположении датчика повторяется каждый раз для каждого параметра.

2) Потенциальная противоречивость (аномалия обновления) заключается в том. что вследствие избыточности данных может возникнуть ситуация, когда информация о местоположении датчика модифицируется, при этом не во всех кортежах эта модификация производится.

3) Аномалия включения: В БД нельзя внести информацию о датчике, который устанавливается на объект, но временно не задействуется. Это связано с тем, что отсутствующие значения параметров можно отметить каким-либо образом, но если атрибут ключевой, то нарушается ограничение на корректность включения.

4) Аномалия удаления: при необходимости удаления всех параметров, в которых был использован некоторый датчик, мы полностью теряем информацию об этом датчике.

Перечисленные выше проблемы могут быть решены, если предложить другую схему, состоящую из двух отношений:

- Поставщик_информации (шифр_датчика, параметр);

- Датчик (шифр_датчика, местоположение).

В данном случае местоположение не вносит избыточности в БД.

Таким образом, противоречия исчезли и единственный недостаток заключается в увеличении времени на реализацию некоторых запросов пользователя.

Для рационального выбора логической схемы БД, минимизации проблем, связанных с избыточностью и аномалиями, необходимо учитывать зависимости, связывающие данные.

Функциональные зависимости (ФЗ) являются отражением семантики взаимосвязи данных в предметной области. С каждым построенным отношением в БД связывается определенная совокупность функциональных зависимостей, которые являются в ряде случаев источником аномалий данных.

· Пусть r - отношение со схемой R - r(R), X Í R(подмножество), Y Í R. Говорят, что отношение r удовлетворяет ФЗ-ти X ® Y, если выполняется ограничение: имеется не более чем один кортеж для каждого значения X из r.

Простейший алгоритм для выявления фз

1) Отсортировать отношение r по столбцам X так, собрать кортежи с равными Х -значениями вместе.

2) Если каждая совокупность кортежей с равными Х - значениями имеет также Y-значения, то в отношении r соблюдается ФЗ X ® Y (из X в Y).

Пример:

Шифр_датчика	Местоположение	Параметр	Подсистема
А1	S1	P1	D
А2	S1	P1	D
А3	D1	P1	D
А4	D2	P3	B
А5	S2	P3	B
А6	S3	P3	B
А7	S3	P2	K

 

Функциональные зависимости:

а) Местоположение ® Параметр - нет ФЗ;

б) Местоположение ® Подсистема - нет ФЗ (из-за S₃);

в) Параметр ® - Подсистема - есть ФЗ.

Полное множество фз

· Для каждого отношения с приписанным ему некоторым набором ФЗ-тей существует вполне определенное множество ФЗ-тей, называемое полным.

· Пусть задано отношение r (A₁,... An) и известно, что в r существуют ФЗ-ти, составляющие множество F.

· Полное множество всех ФЗ-тей, полученное на основе множества F называется замыканием множества F и обозначается F⁺, причем F Í F⁺.

Чтобы построить F⁺ необходимо знать правила вывода одних ФЗ-тей из других.

· Эти правила вывода называют аксиомами вывода функциональных зависимостей.

Аксиомы вывода f - зависимостей

Пусть r (R), X, Y, Z, W Í R.

1. Рефлексивность X ® X.

2. Пополнение: если r удовлетворяет ФЗ-ти X ® Y, то оно удовлетворяет и ФЗ-ти XZ ® Y.

3. Аддитивность: если в отношении r заданы ФЗ-ти X ® Y и X®Z, то существует ФЗ-ть X ® YZ.

4. Проективность: если в отношении r задана ФЗ-ть X ® YZ, то существует ФЗ-ть X ® Y.

5. Транзитивность: если в отношении r заданы ФЗ-ти X ® Y и Y®Z, то существует ФЗ-ть X ® Z.

6. Псевдотранзитивность: если в отношении r заданы ФЗ-ти X®Y и YZ® W, то существует ФЗ-ть XZ ® W.

Данная система аксиом является полной и неизбыточной.