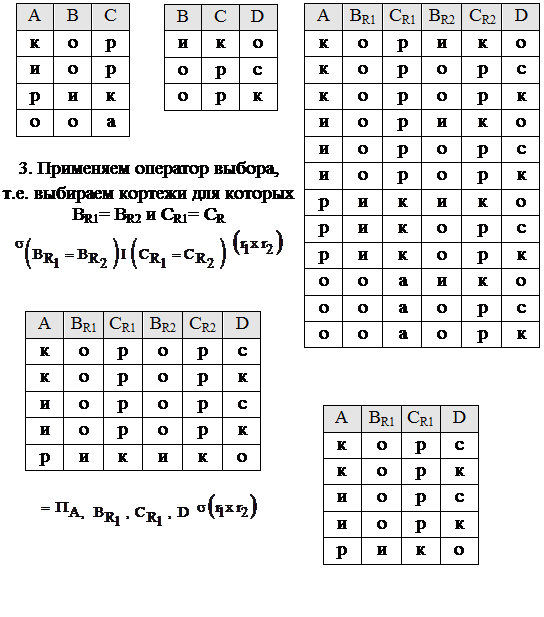Проектирование реляционных баз данных

Основные понятия

Основными понятиями реляционных баз данных являются тип данных, домен, атрибут, кортеж, первичный ключ и отношение.

Тип данных

Понятие тип данных в реляционной модели данных полностью адекватно понятию типа данных в языках программирования. Обычно в современных реляционных БД допускается хранение символьных, числовых данных, битовых строк, специализированных числовых данных (таких как "деньги"), а также специальных временных данных (дата, время, временной интервал). Достаточно активно развивается подход к расширению возможностей реляционных систем абстрактными типами данных (соответствующими возможностями обладают, например, системы семейства Ingres/Postgres). В нашем примере мы имеем дело с данными трех типов: строки символов, целые числа и "деньги".

Домен

Понятие домена более специфично для баз данных, хотя и имеет некоторые аналогии с подтипами в некоторых языках программирования. В самом общем виде домен определяется заданием некоторого базового типа данных, к которому относятся элементы домена, и произвольного логического выражения, применяемого к элементу типа данных. Если вычисление этого логического выражения дает результат "истина", то элемент данных является элементом домена.

 

· Домен - допустимое потенциальное множество значений данного типа.

Пример:

 

Д обозначим домен.

Д₁- множество целых чисел;

Д₂ - множество символьных строк длиной не более 6 символов;

Д₃ - множество символьных строк определенной структуры

ц₁ ц₂ - ц₃ ц₄- ц₅ ц₆, где

ц₁ Î{0, 1, 2, 3}

ц₂ Î{0, 1,..., 9}01 £ ц₁ ц₂ £ 31

 

ц₃ Î{0, 1}

ц₄ Î{0, 1, 2} 01 £ ц₃ ц₄ £ 12

 

ц₅ , ц₆Î{0, 1,..., 9}/

Тогда мы получаем множество дат вида - 21-12-99.

Кортеж, отношение

· Кортеж, соответствующий данной схеме отношения, - это множество пар {имя атрибута, значение}, которое содержит одно вхождение каждого имени атрибута, принадлежащего схеме отношения. "Значение" является допустимым значением домена данного атрибута (или типа данных, если понятие домена не поддерживается). Тем самым, степень или "арность" кортежа, т.е. число элементов в нем, совпадает с "арностью" соответствующей схемы отношения. Попросту говоря, кортеж - это набор именованных значений заданного типа (строка в отношении).

· Отношение R, определенное на доменах Д₁, Д₂,..., Д_К есть множество кортежей арности К следующего вида:

R = { < d_1i, d_2i,..., d_Ki > }, i= 1, 2,... N таких, что

d_1i Î Д₁,..., d_Ki Î Д_К и R является подмножеством декартова произведения доменов

R Í Д₁ х Д₂ х... х Д_N.

Так как отношения являются множествами кортежей, то в них не должны встречаться одинаковые кортежи и порядок кортежей в отношении несущественен.

Обычным представлением отношения является таблица, заголовком которой является схема отношения, а строками - кортежи отношения-экземпляра; в этом случае имена атрибутов именуют столбцы этой таблицы. Поэтому иногда говорят "столбец таблицы", имея в виду "атрибут отношения". Этой терминологии придерживаются в большинстве коммерческих реляционных СУБД.

Для описания структур данных отношения используются в двух аспектах:

- для представления набора объектов:

- для представления связей между данными.

В первом случае кортеж выполняет роль описания атрибутов отдельных объектов. Столбцы отношений соответствуют тем или иным атрибутам объекта.

Пример: Отношение “Датчик”

 

Имя_датчика	Параметр	Тип
Д5	P1	давление

 

Во втором случае кортеж указывает на ассоциацию объектов, связанных между собой определенной семантикой, задаваемой отношениями.

Пример: Принадлежность датчика определенному коммутатору

 

 

 

Отметим, что каждому коммутатору принадлежит по три датчика. Следовательно можно сформировать отношение “Принадлежность”:

 

Имя_К	Имя_1_Дат	Имя_2_Дат	Имя_3_Дат
К1	Д1	Д2	Д3
К2	Д4	Д5	Д6

 

Таким образом, отношение описывает и объект и выражает связи.

· Столбцы отношений называются атрибутами и каждый атрибут выражается своим именем.

Порядок столбцов в отношениях произвольный. От изменения порядка в столбцах суть отношения не меняется.

Для отношения r схемой отношения R является множество{A₁,...,A_K}, A_i - имя атрибута и r (R) º r{A₁,..., A_K}.

Для отношения можно привести следующие аналогии

- схема отношения - формат записи;

- кортеж в отношении - экземпляр записи;

- отношение - файл записей, формат которого соответствует схеме отношений.

Схема отношения, схема базы данных, реляционная база данных

· Схема отношения - это именованное множество пар {имя атрибута, имя домена (или типа, если понятие домена не поддерживается)}. Степень или "арность" схемы отношения - мощность этого множества.

· Схема базы данных (в структурном смысле) - это набор именованных схем отношений.

· Логической схемой БД будем называть совокупность схем отношений

R1 [A11,..., A1K] ... Rm [Am1,..., AmK]

ЛС = {

 

 

· Реляционной БД называют набор экземпляров конечных отношений, построенных в соответствии с логической схемой БД.

Наиболее характерной с различных точек зрения является реляционная МД, так как она имеет возможность гибкого изменения и развития схем, а также логическую ясность представления данных. В связи с этим реляционная МД используется для построения логических схем на основе КС. реляционная модель в одной и той же форме (n-арнарных отношений) позволяет описывать как объекты, так и связи между ними. Кроме того, для реляционных МД хорошо проработан аппарат манипулирования данными (реляционная алгебра). В связи с этим современные СУБД являются системами управления базами данных реляционного типа.

 

 

 

Ключи отношений

· Значение кортежа t на атрибуте А называют t (А) или, другими словами, А - значение кортежа t.

· Если Х Ì R некоторого отношения, тогда t (Х) можно интерпретировать как вхождение кортежа t в атрибуты, определяемые множеством Х.

Среди атрибутов схемы отношений можно выбрать такое подмножество атрибутов К Ì R, что для любого t_i (K) будет выполняться t_i (K) ¹t_j (K), при i¹j.

· Если К - минимальное подмножество атрибутов из R, то К - ключ отношения.

· Отношение может иметь не единственный ключ. Эти ключи называют возможными ключами.

· Множество ключей, выбранных из всех возможных ключей и определенным образом перечисленных, называют выделенными ключами.

Один из выделенных ключей отношения выбирают в качестве первичного.

· Множество К Ì R называют суперключом, если К содержит любой из возможных ключей для r.

· Атрибут А называется первичным, если входит в состав любого из возможных ключей.

Замечание 1:

Конечные отношения могут иметь различные ключи в зависимости от значений и количества кортежей в отношении, но при этом схема отношения не меняется.

Замечание 2:

Понятие ключа задается для схемы отношения, но это необходимо делать с учетом всех возможных состояний отношений с данной схемой.

Манипулирование связями и сущностями может быть реализовано при помощи реляционной алгебры, которая задает операции над отношениями.

Операции над отношениями

Реляционные операторы

Теоретико-множественные операции над отношениями

Два отношения с одной и той же схемой могут быть рассмотрены как подмножества одного и того же множества, составленного из всех возможных кортежей с этой схемой.

Для такого представления могут выполняться теоретико-множественные операторы:

Если r и s со схемой R, то

q (R) = r È s- объединение;

q (R) = r Ç s- пересечение;

q (R) = r - s- вычитание;

r Ç s = r - (r - s).

Арность - размерность. Унарный - размерность 1, бинарный - размерность - 2, n - арный - размерность n.

Оператор выбора

· Выбор - унарная операция, результатом которой является новое отношение с набором кортежей, атрибуты которых удовлетворяют определенному условию:

s_F (r) = q

F - условное выражение, операндами которого являются имена атрибутов, связанных между собой логическими операциями или операциями сравнения.

Пример:

A1 A2 A3 а б в a е а

r q

sF (r): (A1=a) È (A1 =a) A1	A2	A3
а	б	в
a	е	а
и	к	л

Оператор проекции

Это также унарный оператор над отношением. Отличие от “выбора” - этот оператор выбирает не кортежи, а столбцы.

r (R), XÌ R,

P_X (r) = q (X)

Если при этой операции образовались идентичные кортежи, то они удаляются. Операция проекции обладает свойством взаимопоглощения. Если две проекции выполняются последовательно и вторая операция выполняется по отношению к предыдущей операции, то конечный результат будет такой же, как непосредственно к исходному отношению, то есть

 

P_Y (P_X (r)) = P_Y (r)

Пример:

r (A, B, C)Х=(А,В); Y=(А)

A B а б d е и к а б

а) r (A, B, C) П_Х (r) П_Y (r)

A а d и   A	B	C
а	б	в
d	е	а
и	к	л
а	б	д

 

A а d и а

б) r (A, B, C) П_Y (r) П_Y (r)

A а d и   A	B	C
а	б	в
d	е	а
и	к	л
а	б	д

Оператор декартова произведения

Это бинарный оператор, предназначенный для комбинирования двух отношений.

Пусть r₁ отношение арности к₁, r₂ - к₂.

· r = r₁ x r₂ будет представлять из себя множество кортежей арности к₁ + к₂ таких, что первые к₁ элементов кортежа отношения r составляют кортежи отношения r₁, а последующие к₂ элемента кортежа из r составляются кортежами из r₂. Сочетание кортежей из r₁ и r₂ при образовании кортежа r осуществляется по правилам декартова произведения.

Пример:

r₁ r₂ r = r₁ x r₂

а р с и   а б с d   а	б	а	р
а	б	с	и
с	d	а	р
с	d	с	и

Оператор естественного соединения отношений

Это бинарный оператор для комбинирования двух отношений.

Пусть r₁ (R₁) и r₂ (R₂), где

R₁ [A ₁, A ₂,..., A_K, B₁, B₂,..., B_n ]

R₂ [A ₁, A ₂,..., A_K, С₁, С₂,..., С_m ].

Тогда результатом естественного соединения будет отношение:

r = r₁ |> <| r₂=

= П

Пример:

1. r₁ r₂ 2. Сначала строим r = r₁ x r₂

		+ +   + + +

 

Оператор соединения отношений

Пусть r (R) и s (S), где

R [A ₁, A ₂,..., A_k]

S [B₁, B₂,..., B_p].

Тогда оператор соединения отношений:

Ai Q Bj

q(A ₁, A ₂,..., A_k, B₁, B₂,..., B_p) = r |> <| s = s _{Ai Q Bj} (r x s),

 

Q- оператор сравнения (=, >, <, ³, £, ¹)

Если Q - “=”, то соединение называется эквисоединением.

Пример:

А В С D E а б с а и а б с е к а и р а и а и р е к о е ж а и о е ж е к

1. r s 2. Строим r = r x s

		+

 

Оператор деления отношений

Пусть r (R) и s (S), где

R [A ₁, A ₂,..., A_k]

S [B₁, B₂,..., B_p] и B₁ º A_k-p+1,..., B_p º A_m. Знак º обозначает эквивалентность.

Тогда оператор:

При этом q будет иметь схему отношений [A ₁, A ₂,..., A_k-p] и k>p.

Пример:

1. Есть r(A, B, C, D) и s (C, D) 2. П_А,В (r) 3. П_А,В (r) x s

А В C D и о с а и о р к о р с а о р р к с к с а с к р к

А В и о о р с к

А В С D и о р к о р с а с к р к и о с а с к с а и о к с

C D с а р к

	- - - + - -

 

 

4. П_А,В (r) x s - r 5. П_А,В (П_А,В(r) x s - r)

	А В C D о р р к
		А В о р

 

 

6. П_А,В (r) - П_А,В (П_А,В(r) x s - r) = r ¸ s

 

	А В и о с к

 

Замечание: Результатом деления является множество кортежей, полученных путем выделения начальных частей кортежей из r таких. что продолжением этого кортежа являются кортежи из s. деление может использоваться для поиска информации в БД о том, например, в каких подсистемах используются интересующие нас данные.