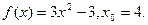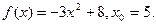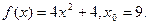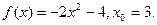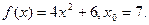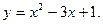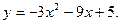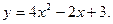Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Красноярский юридический техникумСтр 1 из 5Следующая ⇒
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Красноярский юридический техникум
Сборник задач и упражнений По математике Учебно-методическое пособие для специальности: Земельно–имущественные отношения (базовый курс ПСО)
2010 г.
Пояснительная записка. 3 I.Функция. 4 Понятие функции. Способы задания и свойства. 4 Решение типовых заданий. 6 Упражнения и задания для самостоятельной работы.. 8 II.Предел функции. 11 Методы вычисления пределов функции. 11 Основные теоремы о пределах. 12 Решение типовых заданий. 13 Упражнения и задания для самостоятельной работы.. 18 III.Непрерывность функции. 23 Решение типовых заданий. 24 Упражнения и задания для самостоятельной работы.. 26 Список рекомендуемой литературы.. 31
Пояснительная записка Предлагаемое учебно-методическое пособие предназначено для организации практических занятий и процесса самоподготовки студентов второго курса, обучающихся по специальности 080114 земельно-имущественное хозяйство, изучающих раздел «Функции. Пределы функции. Непрерывность функции». Цель данного методического пособия оказать студентам помощь в овладении методикой решений практических задач по математике. По данному разделу предусматривается 4 практических занятий, в том числе выполнение студентами на последнем занятии аудиторной контрольной работы. Каждое практическое занятие содержит следующие структурные элементы: 1).10-минутная проверочная работа по учебному материалу предыдущего занятия; 2). Теоретическое введение по теме занятия, решение типовых задач; 3). Самостоятельная работа студентов; 4). Методические указания и задания для подготовки к следующему занятию. На 10-минутную проверочную работу и теоретическое введение с решением типовых задач отводится 1 академический час. Второй час отводится на самостоятельную работу и выдачу домашнего задания и указаний для самоподготовки студентов к следующему занятию. Предлагаемые типовые задачи, и задачи для самостоятельного решения составляют набор «обязательных» задач для всех студентов. Дополнительные задачи могут быть предложены наиболее подготовленным студентам.
I. Функция Понятие функции. Способы задания и свойства Определение функции: Если каждому элементу х множество Х (х? Х) ставиться в соответствие вполне определенный элемент у множества y (y? Y), то говорят, что множестве, Х задана функция у=f(х). При этом х называется независимой переменной (или аргументом), у- зависимой переменной, а буква f обозначает закон соответствие. Множество Х называется областью определения (или существования) функции, а множество Y - областью значений функции. Если множество Х специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной х, т.е. множество таких значений х, при которых функция у =f(х) вообще имеет смысл. Например, область определения функции Способы задания функций. Существует несколько способов задания функции. а) Аналитический способ, если функция задана формулой вида у=f(х). Этот способ наиболее часто встречается на практике. Так, функция Не следует смешивать функцию с ее аналитическим выражением. Так, например, одна функция
имеет два аналитических выражения: х2 (при х< 0) и х + 3 (при х б) Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента х и соответствующие значения функции f(х), например таблица логарифмов. в) Графический способ состоит в изображении графика функции — множества точек (х, у) плоскости, абсциссы которых есть значения аргумента х, а ординаты — соответствующие им значения функции у=f(х). г) Словесный способ, если функция описывается правилом ее составления, например, функция Дирихле: f(х)=1, если х рационально; f(х) = 0, если х иррационально. Решение типовых заданий Пример 1. Найти область определения функций а) Решение. а) Область определения функции X найдем из системы неравенств б) Имеем систему
получим
Рисунок 4
Очевидно, что полученные неравенства справедливы при любом Пример 2. Найти область значений функций: Решение. Преобразуем функцию
Так как синус любого угла по абсолютной величине не превосходит 1, т.е. Итак, область значений функции Пример 3. Выяснить четность (нечетность) функций: а) б) в) решение: а) б) Так как в) Так как
Упражнения и задания для самостоятельной работы Теоретические вопросы 1. Что такое функция? 2. Какие существуют способы задания функций? 3. Какую функцию называют периодической? Что такое период функции? 4. Какая функция называется четной? нечетной? 5. Какая функция называется монотонной. Задание 1. Найти область определения функции. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. Задание 2. Найти область значения функции.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
Задание 3. Выяснить четность (нечетность) функции: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
Задание 4. Построить графики функции: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. II. Предел функции. Решение типовых заданий Пример 1. Найти: а) Р е ш е н и е: а) На основании непрерывности функции в точке х=7 искомый предел равен значению функции в этой точке, т.е. б) При в) г) Заметим, что этот предел нельзя вычислять с помощью теоремы о пределе произведения, поскольку В рассмотренных примерах предел находится сразу: в виде числа или символа Пример 2. Найти: а) Р е ш е н и е: а) для раскрытия неопределенности вида
Разложим числитель на множители и сократим дробь множитель (х-1): сокращение возможно, т.к. при
б) Для раскрытия неопределенности вида
Пример 3. Найти: а) в) Р е ш е н и е: а) Имеем неопределенность вида
б) Используя тот же прием, что и в п.а), можно показать, что
Рекомендуем запомнить это правило. в) Имеем неопределенность вида Действительно, разделив и числитель и знаменатель на
г) При
При
д) Для раскрытия неопределенности вида
так как Пример 4. Найти: а) б) в) Решение: а) Для раскрытия неопределенности вида
б) При
Обращаем внимание на то, что при x →
в) Пример 5. Вычислить пределы числовых последовательностей.
Пример 6. Вычислить пределы числовых последовательностей.
Пример 7. Вычислить пределы функций.
Пример 8. Вычислить пределы функций.
Пример 9. Вычислить пределы функций.
Пример 10. Вычислить пределы функций.
Пример 11. Вычислить пределы функций.
Пример 12. Вычислить пределы функций.
Пример 13. Вычислить пределы функций.
Пример 14. Вычислить пределы функций.
Упражнения и задания для самостоятельной работы Теоретические вопросы
III. Непрерывность функции Раскрытие неопределенностей Может случиться, что функция Определение. Операция нахождения предела функции Решение типовых заданий 1. Вычислить предел
отсюда следует, что функция
2. Вычислить предел
Преобразуем функцию
3. Вычислить предел
Преобразуем функцию
4. Вычислить предел
Преобразуем функцию
5. Вычислить предел Преобразуем функцию
так как 6. Вычислить предел Так как
Упражнения и задания для самостоятельной работы Теоретические вопросы 1. Какая функция называется непрерывной в точке? 2. Дайте определение непрерывность сложной функции. 3. Сформулируйте свойства функций, непрерывных в точке. 4. Сформулируйте теорему о непрерывности обратной функций. 5. Что такое скачек функции? Задание 1. Доказать, что функция 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. Задание 2. Пользуясь определением непрерывности "на языке 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. Задание 3. Вычислить пределы функции. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. Список рекомендуемой литературы 1.Берман Г.Н. Сборник задач по курсу математического анализа. М., Наука, 1985. 2.Бугров Я.С., Никольский С.М. Высшая математика. Задачник. М., Наука, 1982. 3.Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Части 1, 2. М.., Высшая школа, 1980. 4.Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). М., Высшая школа, 1994.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.124.232 (0.282 с.) |
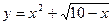 есть полуинтервал
есть полуинтервал 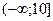 , так как 10–х> если же переменная х обозначает, предположим, время, то при естественном дополнительном условии
, так как 10–х> если же переменная х обозначает, предположим, время, то при естественном дополнительном условии 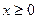 областью определения функции будет отрезок [0; 10].
областью определения функции будет отрезок [0; 10].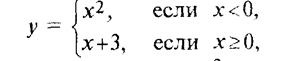
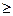 0).
0). ; б)
; б) 
 ; в)
; в) 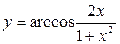 .
. откуда
откуда  или
или  .
. . Решая первое неравенство,
. Решая первое неравенство, ; решая второе, найдем
; решая второе, найдем  , откуда
, откуда  и
и  . С помощью числовой оси (рис.4) находим решение системы неравенств:
. С помощью числовой оси (рис.4) находим решение системы неравенств:  ,т.е. область определения функции
,т.е. область определения функции 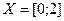 .
.
 в) Область определения найдем из неравенства
в) Область определения найдем из неравенства  , откуда
, откуда 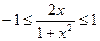 . Так как при любом
. Так как при любом 
 , то перейдем к равносильному неравенству
, то перейдем к равносильному неравенству  , откуда
, откуда , или
, или 
 .
.

 , то
, то  ,
, 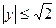 ,
, 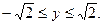




 Так как
Так как  , то данная функция четная;
, то данная функция четная; (после преобразований).
(после преобразований). , то данная функция четная.
, то данная функция четная.
 и
и 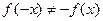 , то данная функция общего вида, т.е. ни четная, ни нечетная.
, то данная функция общего вида, т.е. ни четная, ни нечетная.



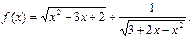

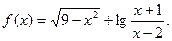

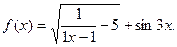






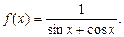















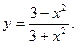






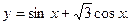


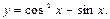
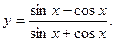

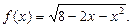



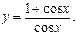



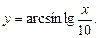
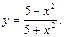
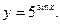

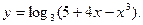


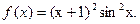
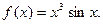
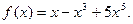


 ;
;
 .
.
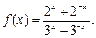


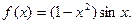
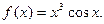
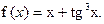








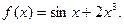


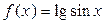


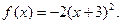










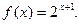


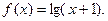

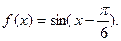

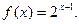







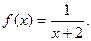


 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.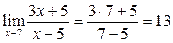 .
. числитель (3х+5) стремится к
числитель (3х+5) стремится к  (т.е. является ограниченной функцией), а знаменатель (х-5) – к нулю (т.е. является бесконечно малой величиной); очевидно, их отношение есть величина бесконечно большая, т.е.
(т.е. является ограниченной функцией), а знаменатель (х-5) – к нулю (т.е. является бесконечно малой величиной); очевидно, их отношение есть величина бесконечно большая, т.е.  .
.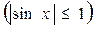 к бесконечно большой величине х (при
к бесконечно большой величине х (при  ) есть величина бесконечно малая.
) есть величина бесконечно малая.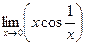 =0, т.к. произведение бесконечно малой величины х (при
=0, т.к. произведение бесконечно малой величины х (при  ) на ограниченную функцию
) на ограниченную функцию  есть величина бесконечно малая.
есть величина бесконечно малая. не существует (при
не существует (при  изменяется непрерывно вдоль числовой оси до бесконечности, при этом значения
изменяется непрерывно вдоль числовой оси до бесконечности, при этом значения  колеблются от -1 до 1 и от 1 до -1, не стремясь ни к какому числу (пределу).
колеблются от -1 до 1 и от 1 до -1, не стремясь ни к какому числу (пределу). . Но чаще при вычислении пределов мы сталкиваемся с неопределенностями, когда результат нахождения предела неясен: например, в случае отношения двух бесконечно малых функций (условное обозначение
. Но чаще при вычислении пределов мы сталкиваемся с неопределенностями, когда результат нахождения предела неясен: например, в случае отношения двух бесконечно малых функций (условное обозначение  ) или бесконечно больших
) или бесконечно больших  . Кроме отмеченных неопределенностей вида
. Кроме отмеченных неопределенностей вида  ,
,  ,
,  ,
,  ,
,  .
. ; б)
; б)  ; в)
; в)  .
.
 (х-1) стремится к нулю, но не равен нулю.
(х-1) стремится к нулю, но не равен нулю. =
=  =
=  =
=  .
. в) Для раскрытия неопределенности вида
в) Для раскрытия неопределенности вида  (тогда
(тогда  , при
, при  =
= 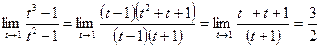 .
. ; б)
; б) 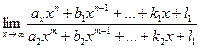 ;
; ; г)
; г) 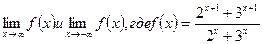 ; д)
; д)  .
. определяется членами с наибольшими показателями степеней (соответственно
определяется членами с наибольшими показателями степеней (соответственно  и
и  ), разделим числитель и знаменатель на
), разделим числитель и знаменатель на  , т.е. на х с наибольшим показателем степени числителя и знаменателя. Используя теоремы о пределах, получим:
, т.е. на х с наибольшим показателем степени числителя и знаменателя. Используя теоремы о пределах, получим: .
. , т.е. предел отношения двух многочленов
, т.е. предел отношения двух многочленов  равен 0, отношению коэффициентов при старших степенях х или
равен 0, отношению коэффициентов при старших степенях х или  , а в знаменателе степень m =2; т.к.
, а в знаменателе степень m =2; т.к.  , то на основании правила, сформулированного в п.б), искомый предел равен
, то на основании правила, сформулированного в п.б), искомый предел равен  , получим:
, получим: .
. , при этом поведение числителя и знаменателя определяется вторыми слагаемыми, которые возрастают быстрее первых. Разделив числитель и знаменатель на
, при этом поведение числителя и знаменателя определяется вторыми слагаемыми, которые возрастают быстрее первых. Разделив числитель и знаменатель на 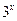 и используя теоремы о пределах, получим:
и используя теоремы о пределах, получим: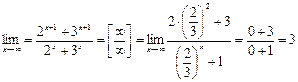 , поскольку
, поскольку  .
. имеем неопределенность вида
имеем неопределенность вида  , при этом поведение числителя и знаменателя определяется первыми слагаемыми, которые убывают медленнее других. Разделив числитель и знаменатель на
, при этом поведение числителя и знаменателя определяется первыми слагаемыми, которые убывают медленнее других. Разделив числитель и знаменатель на  и используя теоремы о пределах, получим:
и используя теоремы о пределах, получим: .
.

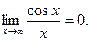




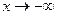 имеем неопределенность вида
имеем неопределенность вида 
 в знаменателе нет неопределенности, так как он представляет сумму бесконечно больших положительных величин – величину, бесконечно большую.
в знаменателе нет неопределенности, так как он представляет сумму бесконечно больших положительных величин – величину, бесконечно большую.





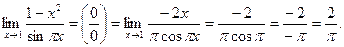
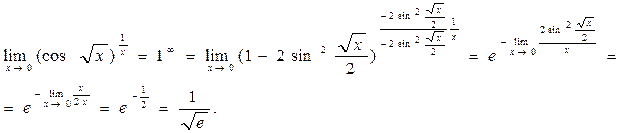




 определена и непрерывна всюду, за исключением некоторого значения
определена и непрерывна всюду, за исключением некоторого значения 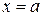 , при котором функция
, при котором функция  в этом случае называется раскрытием неопределенности, а сам предел
в этом случае называется раскрытием неопределенности, а сам предел  , если он существует, называется истинным значением функции
, если он существует, называется истинным значением функции  .
. ,
, не определена, а значит разрывна в точке
не определена, а значит разрывна в точке 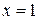 . Выполним некоторые преобразования этой функции, а именно вынесем общий множитель знаменателя дроби за скобку. Получим:
. Выполним некоторые преобразования этой функции, а именно вынесем общий множитель знаменателя дроби за скобку. Получим: .
. .
. .
. , а именно применим формулу сокращенного умножения.
, а именно применим формулу сокращенного умножения. .
.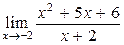 .
.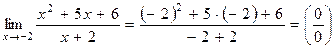 ,
, , а именно разложим на множители квадратный трехчлен, находящийся в числителе, используя теорему Виета.
, а именно разложим на множители квадратный трехчлен, находящийся в числителе, используя теорему Виета. .
. .
.
 , а именно используем умножение числителя и знаменателя на число сопряженное.
, а именно используем умножение числителя и знаменателя на число сопряженное.



 .
. , используя «замечательный предел»
, используя «замечательный предел» . Получим
. Получим ,
, и
и  , то
, то  .
. .
.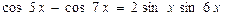 , то
, то .
. непрерывна в точке
непрерывна в точке 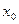 (найти
(найти  ).
).