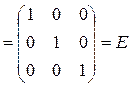Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Богряшова А.Г., Ганенкова И.С., Курбатова Л.П.,Содержание книги
Поиск на нашем сайте
Богряшова А.Г., Ганенкова И.С., Курбатова Л.П., Математика: Учебное пособие для студентов очной и заочной форм обучения/Под редакцией к.т.н., доц. Просвирова А.Э. – 2-е изд., перераб. и доп. – Волгоград: ___________, 2009. – 48с. Адресовано студентам очной и заочной форм обучения экономических вузов, изучающих математику. Задачи, представленные в пособии, имеют экономическое содержание и демонстрируют возможности применения математических методов в решении проблем практической деятельности специальностей: менеджмент организации(080507), коммерция(торговое дело)(080301), маркетинг(080111), товароведение и экспертиза товаров(080401), бухгалтерский учёт, анализ и аудит(080109), экономика и управление на предприятии(торговли)(080502), мировая экономика(080102), финансы и кредит(080105).
ОГЛАВЛЕНИЕ Введение......................................................................................................... 4 Глава 1. Варианты контрольных заданий................................................... 5 Задача № 1................................................................................................. 5 Задача № 2................................................................................................. 9 Задача № 3............................................................................................... 10 Задача № 4............................................................................................... 14 Задача № 5............................................................................................... 15 Задача №6................................................................................................ 16 Задача №7................................................................................................ 17 Задача №8................................................................................................ 19 Глава 2. Примеры решения задач.............................................................. 21 Задача № 1............................................................................................... 21 Задача № 2............................................................................................... 27 Задача № 3............................................................................................... 29 Задача № 4............................................................................................... 32 Задача № 5............................................................................................... 35 Задача №6................................................................................................ 37 Задача №7................................................................................................ 41 Задача №8................................................................................................ 43 Приложения................................................................................................. 46 1. Таблица производных......................................................................... 46 2. Таблица интегралов............................................................................ 46 3. Достаточный признак экстремума функции двух переменных......... 47 4. Основные замены переменной в неопределенном интеграле............ 47 4. Основные интегралы, интегрируемые по частям............................... 47 5. Таблица значений функции ex............................................................. 48 Список рекомендуемой литературы........................................................... 49
Введение В настоящем пособии представлены задачи по учебной дисциплине «Математика», изучаемого студентами всех специальностей Волгоградского филиала Московского государственного университета коммерции на протяжении двух семестров первого года обучения. Предлагаемое вашему вниманию учебное пособие состоит из двух глав и приложения. В первой главе представлены варианты контрольных заданий. Каждое контрольное задание включает в себя 8 задач по основным разделам курса математики для экономических вузов. Все без исключения задачи имеют экономическое содержание и демонстрируют возможности применения математических методов к решению проблем практической деятельности коммерсанта, менеджера, экономиста. К каждой задаче предлагаются 20 вариантов для самостоятельного решения. Номер варианта назначается преподавателем. В приложении приведена справочная информация, необходимая для решения задач. Следует отметить, что в Волгоградском филиале РГТЭУ студенты заочной формы обучения течение первого года занятий по учебному плану должны выполнить две контрольных работы. В пособии представлены задачи по обеим контрольным работам; выбор номеров задач для каждой из них остается за преподавателем. Во второй главе пособия приводится подробный образец решения и оформления контрольных заданий. Большое внимание уделяется экономической интерпретации полученных результатов. Хотя учебное пособие предназначено в первую очередь для студентов заочной формы обучения, авторы надеются, что оно будет полезно студентам всех форм обучения, изучающих математику. Глава 1. Варианты контрольных заданий Задача № 1 Предприятие специализируется по выпуску продукции трех видов P1, P2, и P3; при этом использует сырье трех типов: S1, S2 и S3. Норма и объем расхода каждого типа сырья на 1 день заданы таблицей. Найти ежедневный объем выпуска каждого вида продукции. Полученную систему уравнений решить матричным методом, методом Гаусса и методом Крамера.
Задача № 2 Определить, имеет ли матрица A обратную, и если имеет, то вычислить ее: 1. 5. 9. 13. 17. Задача № 3 В таблице приведены данные об исполнении баланса. Используя модель Леонтьева многоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной сохранится на прежнем уровне.
Задача № 4 В результате маркетингового исследования установлено, что функции спроса и предложения имеют вид:
где p – цена товара. Найти: 1) Равновесную цену p0. 2) Эластичность спроса и предложения для этой цены. 3) Изменение дохода при увеличении цены на 5% от равновесной. Задача № 5 Фирма реализует произведенную продукцию по цене p, а зависимость издержек C имеет вид Используя методы дифференциального исчисления: 1) выполнить полное исследование функции зависимости прибыли фирмы П от объема производства q построить ее график. 2) Найти оптимальный для фирмы объем выпуска продукции и соответствующую ему прибыль. Вариант №1 a=70; b=0,002; c=100; p=100 Вариант №2 a=50; b=0,001; c=30; p=60 Вариант №3 a=10; b=0,002; c=40; p=20 Вариант №4 a=15; b=0,001; c=5; p=30 Вариант №5 a=18; b=0,005; c=30; p=40 Вариант №6 a=40; b=0,006; c=20; p=60 Вариант №7 a=80; b=0,007; c=10; p=90 Вариант №8 a=80; b=0,008; c=15; p=110 Вариант №9 a=15; b=0,009; c=100; p=85 Вариант №10 a=25; b=0,01; c=35; p=105 Вариант №11 a=40; b=0,011; c=5; p=80 Вариант №12 a=50; b=0,012; c=15; p=90 Вариант №13 a=100; b=0,013; c=0; p=110 Вариант №14 a=100; b=0,014; c=140; p=200 Вариант №15 a=150; b=0,015; c=150; p=210 Вариант №16 a=160; b=0,016; c=250; p=300 Вариант №17 a=170; b=0,017; c=10; p=270 Вариант №18 a=180; b=0,018; c=30; p=200 Вариант №19 a=190; b=0,019; c=150; p=300 Вариант №20 a=200; b=0,02; c=80; p=250 Задача №6 Производственная функция фирмы представляет собой функцию Кобба-Дугласа:
где: K —объем основных фондов в (руб.); L —объем трудовых ресурсов (чел.); Y —объем выпуска продукции в (руб.); A, α, β>0 —постоянные величины, причем α+ β≤1. Известно также, что увеличения выпуска продукции на a% можно достичь или увеличением основных фондов на b% или увеличением численности работников на c%. В настоящее время один работник производит за месяц продукции на M руб, а объем основных фондов оценивается в К руб.Период амортизации основных фондов N месяцев, а месячная зарплата a руб. в месяц. Найдите: 1) явный вид производственной функции этой фирмы; 2)оптимальный размер фирмы, т.е. численные значения K и L, обеспечивающие максимальную прибыль. Вариант 1 a=1, b=2, c=3, M=103, L=103, K=105, N=5, s=1000. Вариант 2 a=1, b=3, c=2, M=104, L=53, K=106, N=5, s=100. Вариант 3 a=1, b=3, c=3, M=104, L=103, K=106, N=3, s=10. Вариант 4 a=1, b=2, c=4, M=104, L=53, K=105, N=2, s=1000. Вариант 5 a=2, b=5, c=5, M=104, L=25, K=107, N=2, s=100. Вариант 6 a=2, b=5, c=4, M=103, L=104, K=107, N=4, s=10. Вариант 7 a=3, b=6, c=9, M=103, L=103, K=109, N=12, s=1000. Вариант 8 a=2, b=4, c=6, M=104, L=103, K=1011, N=18, s=10000. Вариант 9 a=1, b=2, c=3, M=103, L=103, K=107, N=6, s=1000. Вариант 10 a=2, b=4, c=6, M=103, L=103, K=103, N=12, s=1000. Вариант 11 a=2, b=6, c=6, M=103, L=103, K=106, N=6, s=1000. Вариант 12 a=1, b=3, c=2, M=103, L=102, K=105, N=6, s=1000. Вариант 13 a=1, b=3, c=2, M=103, L=60, K=106, N=4, s=1000. Вариант 14 a=3, b=8, c=8, M=104, L=102, K=105, N=12, s=10000. Вариант 15 a=2, b=5, c=4, M=104, L=20, K=105, N=8, s=10000. Вариант 16 a=1, b=2, c=3, M=103, L=103, K=105, N=5, s=1000. Вариант 17 a=2, b=4, c=6, M=104, L=103, K=1011, N=18, s=10000. Вариант 18 a=1, b=3, c=2, M=104, L=53, K=106, N=5, s=100. Вариант 19 a=1, b=3, c=3, M=104, L=103, K=106, N=3, s=10. Вариант 20 a=1, b=2, c=4, M=104, L=53, K=105, N=2, s=1000. Задача №7 Инвестор вложил в производство R0 тыс.руб. и в течение n лет планирует непрерывно увеличивать объем инвестиций на a тыс. руб. ежегодно. Ожидаемая доходность инвестиций составляет i% годовых. Определите 1) современную стоимость такого проекта по формуле 2) наращенную сумму такого потока платежей по формуле Примечание: Современная (текущая, капитализированная) стоимость является одним из важнейших понятий в количественном анализе финансовых операций. Большинство аналитических методов оценки эффективности инвестиционных проектов, кредитных операций основаны именно на определении этой величины. Наращением или ростом денежной суммы называют процесс увеличения суммы денег в связи с присоединением процентов. Вариант 1 R0=11; a=1; n=4; i=1 Вариант 2 R0=12; a=2; n=3; i=2 Вариант 3 R0=13; a=3; n=2; i=3 Вариант 4 R0=14; a=4; n=3; i=4 Вариант 5 R0=15; a=5; n=4; i=5 Вариант 6 R0=16; a=6; n=5; i=6 Вариант 7 R0=17; a=7; n=6; i=7 Вариант 8 R0=18; a=8; n=7; i=8 Вариант 9 R0=19; a=9; n=6; i=9 Вариант 10 R0=20; a=10; п=4; i=10 Вариант 11 R0=21; a=11; n=4; i=11 Вариант 12 R0=22; a=12; n=3; i=12 Вариант 13 R0=23; a=13; n=4; i=13 Вариант 14 R0=24; a=14; n=5; i=14 Вариант 15 R0=25; a=15; n=6; i=15 Вариант 16 R0=26; a=16; n=7; i=16 Вариант 17 R0=27; a=17; n=8; i=17 Вариант 18 R0=28; a=18; n=5; i=18 Вариант 19 R0=29; a=19; n=3; i=18 Вариант 20 R0=30; a=20; n=8; i=20 Задача №8 Рассматривается рынок одного товара; время считается непрерывным. Пусть d(t), s(t), p(t), - соответственно спрос, предложение и цена этого товара в момент t. И спрос и предложение считаются линейными функциями цены: s (р)=α+βρ, α<0, β>0, т.е. предложение с ростом цены растёт. Естественно считать, что а >0, т.е. при нулевой цене спрос имеется (иначе говоря, товар желателен). Основное предположение состоит в том, что цена изменяется в зависимости от соотношений между спросом и предложением: Δ p -γ(ds)Δ t, где γ>0, т.е. увеличение цены прямо пропорционально превышению спроса над предложением и длительности этого превышения. Итак, получаем дифференциальное уравнение: Подставляя в это уравнение линейные зависимости спроса и предложения от цены, получаем линейное неоднородное дифференциальное уравнение с начальным условием.
Уравнение (1) имеет стационарную точку Видно, что Отсюда следует, что lim p(t)=p*. t→∞ В этом случае при p*< p цена стремится к p* возрастая, а при p*> p цена стремится к p* убывая. Сама цена p* есть равновесная цена (спрос равен предложению): d(p)=s(p) => a-bp=α+βρ => Обычный метод решения уравнения (1) - метод вариации постоянной. Согласно этому методу общее решение есть сумма общего решения соответствующего однородного уравнения Решение дифференциального уравнения (1) с начальным условием имеет вид: p(t)= p0 e-γ(b+β) t +
Вариант 1. q 0=8, q 1=2, s 0=-6, s 1=2, p(0)=p0 =1,5, k=0,5 Вариант 2. q 0=10, q 1=3, s 0=-4, s 1=3, p(0)=p0 =2,5, k=0,5 Вариант 3. q 0=12, q 1=6, s 0=-2, s 1=4, p(0)=p0 =2, k=0,5 Вариант 4. q 0=9, q 1=4, s 0=-5, s 1=3, p(0)=p0 =1,5, k=0,5 Вариант 5. q 0=8, q 1=2, s 0=-1, s 1=1, p(0)=p0 =2,5, k=0,5 Вариант 6. q 0=9, q 1=3, s 0=-1, s 1=2, p(0)=p0 =1,5, k=0,5 Вариант 7. q 0=7, q 1=2, s 0=-5, s 1=1, p(0)=p0 =3,5, k=0,5 Вариант 8. q 0=5, q 1=1, s 0=-1, s 1=2, p(0)=p0 =1,5, k=0,5 Вариант 9. q 0=9, q 1=2, s 0=-2, s 1=3, p(0)=p0 =2, k=0,5 Вариант 10. q 0=11, q 1=3, s 0=-1, s 1=3, p(0)=p0 =1,5, k=0,5 Вариант 11. q 0=6, q 1=1, s 0=-2, s 1=3, p(0)=p0 =1,5, k=0,5 Вариант 12. q 0=9, q 1=3, s 0=-2, s 1=2, p(0)=p0 =2, k=0,5 Вариант 13. q 0=15, q 1=2, s 0=-3, s 1=4, p(0)=p0 =2,5, k=0,5 Вариант 14. q 0=13, q 1=5, s 0=-1, s 1=2, p(0)=p0 =1,5, k=0,5 Вариант 15. q 0=8, q 1=1, s 0=-1, s 1=2, p(0)=p0 =2,5, k=0,5 Вариант 16. q 0=14, q 1=3, s 0=-2, s 1=5, p(0)=p0 =1,5, k=0,5 Вариант 17. q 0=10, q 1=2, s 0=-2, s 1=2, p(0)=p0 =2,5, k=0,5 Вариант 18. q 0=15, q 1=3, s 0=-1, s 1=5, p(0)=p0 =1,5, k=0,5 Вариант 19. q 0=16, q 1=5, s 0=-2, s 1=4, p(0)=p0 =1,5, k=0,5 Вариант 20. q 0=13, q 1=2, s 0=-2, s 1=3, p(0)=p0 =2,5, k=0,5 Глава 2. Примеры решения задач Задача № 1 Предприятие специализируется по выпуску продукции трех видов P1, P2, и P3; при этом использует сырье трех типов: S1, S2 и S3. Норма и объем расхода каждого типа сырья на 1 день заданы таблицей. Найти ежедневный объем выпуска каждого вида продукции. Полученную систему уравнений решить матричным методом, методом Гаусса и методом Крамера.
Решение Пусть ежедневно фабрика выпускает x1 шт изделия S1, x2 шт изделия S2 и x3 шт изделия S3. Запишем это в виде столбца суточного выпуска продукции X. Далее выпишем матрицу технико-экономических коэффициентов A, а также столбец суточного расхода сырья В
Найдем количество сырья S1 , затраченного на производство обуви:
Найдем количество сырья S2 , затраченного на производство обуви:
Найдем количество сырья S3 , затраченного на производство обуви:
В результате получаем следующую систему уравнений для определения суточного выпуска продукции:
Задача № 2 Определить, имеет ли матрица A обратную, и если имеет, то вычислить ее:
Решение 1) Вычисляем определитель матрицы А, применяя теорему Лапласа к первой строке:
2) Выписываем транспонированную матрицу АТ:
3) Строим присоединенную матрицу
Выписываем присоединенную матрицу: 4) Находим обратную матрицу по формуле:
Проверка. Воспользуемся определением обратной матрицы
Задача № 3 В таблице приведены данные об исполнении баланса. Используя модель Леонтьева многоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной в 1,2 раза.
Решение 1) Вычисляем коэффициенты прямых затрат aij, показывающие, какой объем продукции i -ой о
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.150 (0.012 с.) |

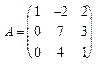 , 2.
, 2.  , 3.
, 3. 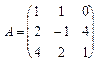 , 4.
, 4. 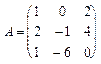 ,
, , 6.
, 6. 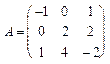 , 7.
, 7.  , 8.
, 8.  ,
,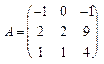 , 10.
, 10. 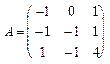 , 11.
, 11.  , 12.
, 12. 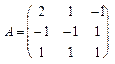
 , 14.
, 14. 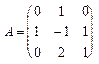 , 15.
, 15.  , 16.
, 16. 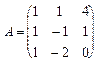 ,
,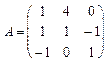 , 18.
, 18.  , 19.
, 19. 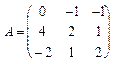 , 20.
, 20. 
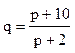 - спроса,
- спроса,
 - предложения,
- предложения,
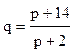 - спроса,
- спроса,
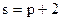 - предложения,
- предложения,
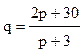 - спроса,
- спроса,
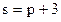 - предложения,
- предложения,
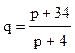 - спроса,
- спроса,
 - предложения,
- предложения,
 - спроса,
- спроса,
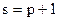 - предложения,
- предложения,
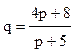 - спроса,
- спроса,
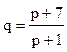 - спроса,
- спроса,
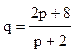 - спроса,
- спроса,
 - спроса,
- спроса,
 - спроса,
- спроса,
 - спроса,
- спроса,
 - спроса,
- спроса,
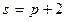 - предложения,
- предложения,
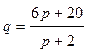 - спроса,
- спроса,
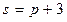 - предложения,
- предложения,
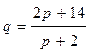 - спроса,
- спроса,
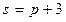 - предложения,
- предложения,
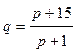 - спроса,
- спроса,
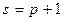 - предложения,
- предложения,
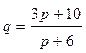 - спроса,
- спроса,
 - спроса,
- спроса,
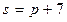 - предложения,
- предложения,
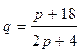 - спроса,
- спроса,
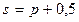 - предложения,
- предложения,
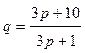 - спроса,
- спроса,
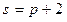 - предложения,
- предложения,
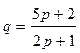 - спроса,
- спроса,

 ,
,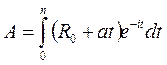 .
.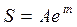
 т.е. спрос с ростом цены падает,
т.е. спрос с ростом цены падает, .
.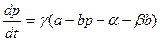 ;
;  , p (0)= p0 (1)
, p (0)= p0 (1) , p* >0.
, p* >0.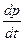 >0 при p* > p и
>0 при p* > p и 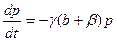 и какого - нибудь частного решения неоднородного уравнения (1).
и какого - нибудь частного решения неоднородного уравнения (1).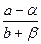 (1 -e-γ(b+β) t) или p(t)= p0 e-γ(b+β) t + p* (1 -e-γ(b+β) t).
(1 -e-γ(b+β) t) или p(t)= p0 e-γ(b+β) t + p* (1 -e-γ(b+β) t).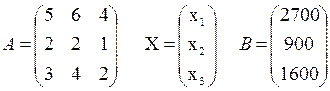
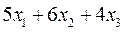 .
.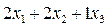 .
. .
.




 . Ее элементы представляют собой алгебраические дополнения соответствующих элементов транспонированной матрицы АТ.
. Ее элементы представляют собой алгебраические дополнения соответствующих элементов транспонированной матрицы АТ.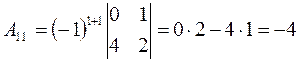





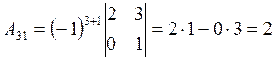
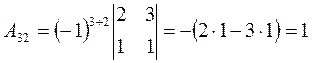

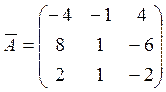
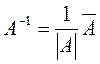

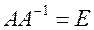 :
: