
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное исчисление функции одной переменной.Содержание книги
Поиск на нашем сайте
Задачи, приводящие к понятию производной. Определение производной. Правила нахождения производной: производная алгебраической суммы, произведения, частного, производная сложной функции. Основные формулы для вычисления производных. Понятие дифференциала. Свойства дифференциала и его вычисление. Производные и дифференциалы высших порядков. Основные теоремы о дифференцируемых функциях и их приложения: экстремум функции, наибольшее и наименьшее значение функции, выпуклость функции. Схема исследования функции и построение графика. Вопросы для самоконтроля. 12. Дать определения производной функции, ее геометрический и физический смысл. 13. Основные правила дифференцирования функции. Правило дифференцирования сложной функции. 14. Дать определение дифференциала функции и его геометрический смысл и основные свойства. 15. Какие функции называются возрастающими и убывающими, сформулировать признаки возрастания и убывания функции. 16. Назвать достаточные признаки экстремума функции. 17. Производные и дифференциалы высших порядков. 18. Какая кривая называется выпуклой, вогнутой, как определяются интервалы выпуклости и вогнутости кривой. 19. Достаточный признак существования точек перегиба. 20. Дать определение асимптоты кривой, нахождение вертикальных и наклонных асимптот. 21. Назвать схему исследования функции и построения ее графика. 22. Применение правила Лопиталя при вычислении пределов функции. Дифференциальное исчисление функции нескольких переменных. Определение функции нескольких переменных. Предел и не прерывность функции нескольких переменных. Частные производные функции нескольких переменных, их геометрический смысл (для случая двух независимых переменных). Частные производные высших порядков. Полный дифференциал функции нескольких переменных, его применение в приближенных вычислениях. Экстремум функции нескольких переменных. Нахождение наибольшего и наименьшего значений. Классические методы оптимизации. Функции спроса и предложения. Функции полезности. Кривые безразличия. Вопросы для самоконтроля. 23. Дать определения функции двух переменных. Что является областью функции двух переменных. 24. Дать определения частных производных первого порядка функции двух переменных.
25. Нахождение частных производных второго порядка функции двух переменных. 26. Полный дифференциал функции нескольких переменных, его применение в приближенных вычислениях. 27. Экстремум функции нескольких переменных. 28. Нахождение наибольшего и наименьшего значений. 29. Функции спроса и предложения. 30. Функции полезности. 31. Кривые безразличия. Интегральное исчисление. Понятие первообразной функции и неопределенного интеграла. Основные свойства неопределенного интеграла. Таблица основных интегралов. Основные методы интегрирования: непосредственное интегрирование, подведение под знак дифференциала, замена переменной, интегрирование по частям. Интегрирование простейших рациональных дробей. Интегрирование некоторых видов иррациональностей. Интегрирование тригонометрических функций. Понятие определенного интеграла. Его геометрический и экономический смысл. Основные свойства определенного интеграла. Формула Ньютона-Лейбница для вычисления определенного интеграла. Замена переменной и интегрирование по частям в определенном интеграле. Несобственные интегралы. Применение определенного интеграла в экономике. Вопросы для самоконтроля. 32. Дать определения неопределенного интеграла и перечислить его основные свойства. 33. Основные методы интегрирования (замена переменных, интегрирование по частям, подведения под знак дифференциала). 34. Понятие определенного интеграла. 35. Геометрический и экономический смысл определенного интеграла. 36. Формула Ньютона-Лейбница. 37. Замена переменных в определенном интеграле. 38. Интегрирование по частям в определенном интеграле. 39. Несобственные интегралы. Задания к контрольной работе. Контрольная работа должна быть выполнена в соответствии с вариантом, выбираемым по последней цифре номера зачетной книжки. При этом, если предпоследняя цифра учебного шифра нечетная (1, 3, 5, 7, 9), то номера заданий для соответствующего варианта даны в таблице 1. Если предпоследняя цифра четная или нуль (2, 4, 6, 8, 0), то номера задач даны в таблице 2. Каждая задача должна содержать условие, подробное решение и ответ. Таблица 1
Таблица 2
1. Введение в математический анализ Найти пределы функций:
11. а) 12. а)
13.
14.
15.
16.
17.
18.
19.
20.
2. Дифференциальное исчисление функции одной переменной. Найти производные данных функций. 21. а) г) y = 2 x - arcsin x; д) 22. а) г) y = e cos 23. а) y = в) y = ln 24. а) y = 25. а) y = 2x3 - г) y = 2 cos 26. а) y = г) y = 2 27. а) 28. а) y = 3x4 – г) y =(x2 - x) 29. а) y = 30. а) y = 31. а) y = 32. а) y = (x2 – 1)ex; б) y = 33. а) 34. а) y = г) y = 35. а) y = 36. а) y = г) 37. а) г) y = 38. а) y = г) y = 3x4 – 39. а) г) 40. а) Исследовать функцию и построить ее график. 41. 45. 49. 53. 57. 3. Дифференциальное исчисление функции нескольких переменных. Найти экстремумы функции. 61. 62. 63. 64. 65. 66. 67. 68. 69. 70. Найти наибольшее и наименьшее значение функции 71.
72. 73.
74. 75.
76. 77. 78. 79. 80. 4. Интегральное исчисление. № 81. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 82. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 83. 1. Найти неопределенные интегралы. 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 84. 1. Найти неопределенные интегралы.
2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 85. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 86. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 87.
1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 88. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 89. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 90. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы или доказать, что они расходятся.
№91. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 92. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 93. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 94. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 95. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 96. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 97. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 98. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 99. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы, если они сходятся.
№ 100. 1. Найти неопределенные интегралы. а) 2. Вычислить определенные интегралы.
3. Найти несобственные интегралы или доказать, что они расходятся.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.28.56 (0.01 с.) |

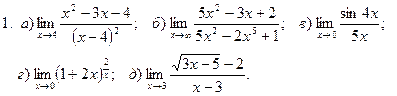



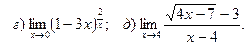




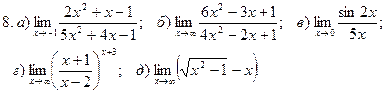

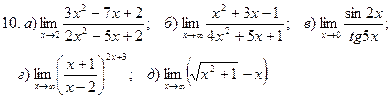 .
.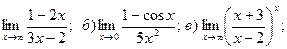

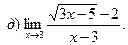
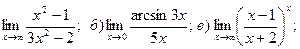

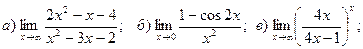

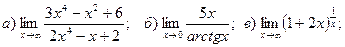
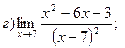

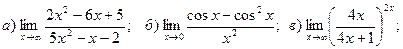

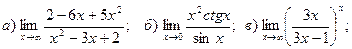
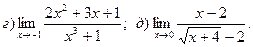
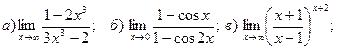
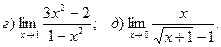

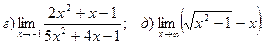
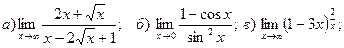
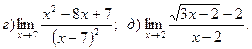
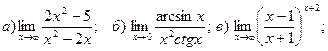

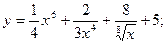 б)
б)  в) y =
в) y =  ;
;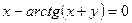 .
. ; б) y =
; б) y = 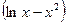
 ; в) y =
; в) y = 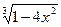 ;
;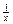 ; д)
; д) 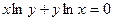 .
.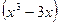 lnx; б)) y =
lnx; б)) y =  x7 +
x7 + 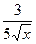 + 1;
+ 1; ; г) y = 2
; г) y = 2 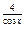 ; д)
; д) 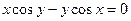 .
.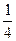 x8 +
x8 + 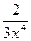 +
+  + 5; б) y =
+ 5; б) y =  ; в) y =
; в) y =  ; г) y = 3 x - arcsin x; д)
; г) y = 3 x - arcsin x; д) 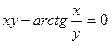
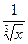 + ex; б) y =
+ ex; б) y = 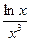 ; в) y =
; в) y = 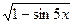 ;
; .
.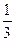 x3 +
x3 +  .
.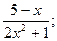 д)
д)  .
.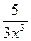 – 9
– 9  + 9; б)y =
+ 9; б)y = 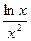 ; в) y = sin tg
; в) y = sin tg  ;
; ; д)
; д) 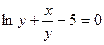 .
.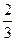 x3 –
x3 – 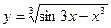 ; в) y = 5 sin3x; г)
; в) y = 5 sin3x; г)  ; д)
; д) 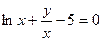 .
.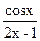 ; д)
; д) 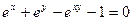 .
. ; б)
; б) 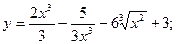 в) y = 5 sin3x + 2; г)
в) y = 5 sin3x + 2; г) 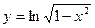 ; д)
; д) 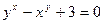 .
. ; д)
; д) 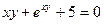 .
.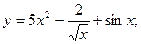 б)
б) 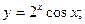 в)
в) 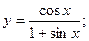 г)
г)  д)
д) 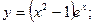 е)
е) 
 ;
; x5 –
x5 – 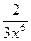 +
+ 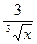 + 2; д)
+ 2; д)  .
. б)
б)  в)
в) 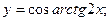 г)
г) 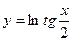 ; д) y = (e5x – 1)6; е)
; д) y = (e5x – 1)6; е) 
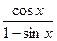 ; в)
; в) 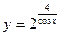 ;
; д)
д)  .
.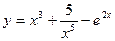 ; б) y =
; б) y =  ; д)
; д) 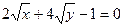 .
.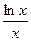 ; б) y = sin tg
; б) y = sin tg  .
.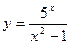 ; б)
; б)  ; в) y = 5 sin3x;
; в) y = 5 sin3x;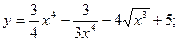 д)
д) 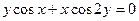
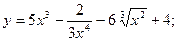 б) y =
б) y =  ; в) y = x
; в) y = x  .
.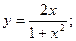 42.
42.  43.
43. 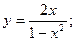 44.
44. 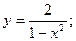
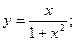 46.
46.  47.
47. 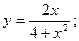 48.
48. 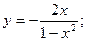
 50.
50. 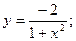 51.
51. 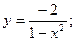 52.
52. 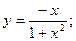
 54.
54. 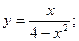 55.
55.  56.
56. 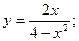
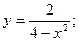 58.
58. 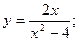 59.
59. 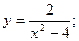 60.
60. 
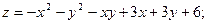


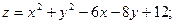
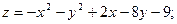

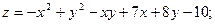


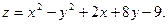
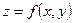 в данной замкнутой области.
в данной замкнутой области. в прямоугольнике
в прямоугольнике
 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 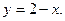
 в прямоугольнике
в прямоугольнике
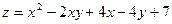 в области, ограниченной параболой
в области, ограниченной параболой 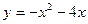 и осью абсцисс.
и осью абсцисс.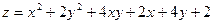 в квадрате
в квадрате
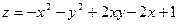 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 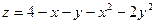 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 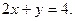
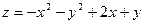 в треугольнике, ограниченном осями координат и прямой
в треугольнике, ограниченном осями координат и прямой 
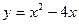 и осью абсцисс.
и осью абсцисс.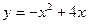 и осью абсцисс.
и осью абсцисс. б)
б) 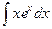 ; в)
; в) 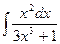 .
.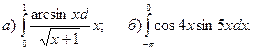
 .
.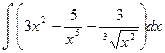 ; б)
; б)  в)
в) 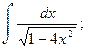 г)
г) 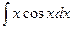 .
.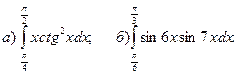
 .
.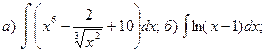
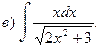
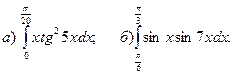
 .
.
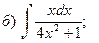 в)
в) 
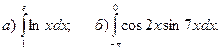
 .
.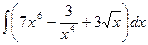 ; б)
; б) 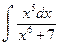 ; в)
; в) 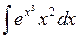 .
.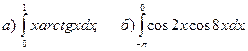 .
.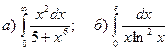 .
. ; б)
; б)  ; в)
; в) 
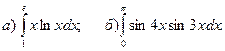
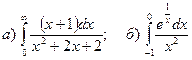 .
.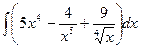 ; б)
; б) 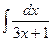 ; в)
; в) 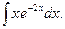

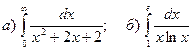 .
.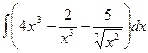 ; б)
; б) 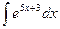 ; в)
; в)  .
.
 .
.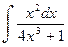 ; в)
; в) 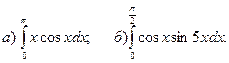
 .
.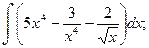 б)
б) 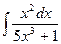 .
.
 .
. ; б)
; б)  в)
в) 
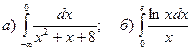 .
. б)
б) 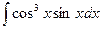 ; в)
; в)  .
.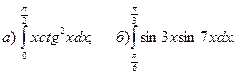
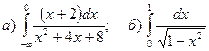 .
. б)
б)  ; в)
; в) 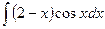 .
.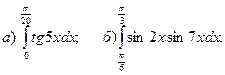
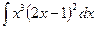 ; б)
; б) 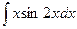 ; в)
; в) 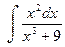 .
.
 б)
б) 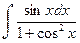 ; в)
; в) 
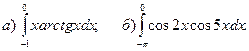 .
. б)
б) 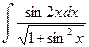 ; в)
; в) 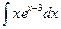 .
.
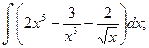 б)
б)  в)
в)  .
.
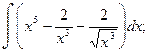 б)
б) 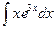 ; в)
; в) 
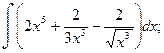 б)
б) 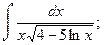 в)
в) 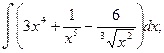 б)
б) 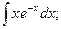 в)
в) 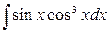 .
.


