
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Функции нескольких переменных.Содержание книги
Поиск на нашем сайте
Определение. Если каждой паре независимых друг от друга чисел Определение. Областью определения функции z называется совокупность пар Область определения функции двух переменных
Рис.1 Частные производные. Частная производная функции
Частная производная функции
Пример 20. Найти частные производные функций.
Частные производные второго порядка. Частные производные второго порядка – это частные производные от частных производных первого порядка. Для функции двух переменных вида
Частные производные второго порядка, в которых дифференцирование производится по разным переменным, называют смешанными производными. Смешанные производные второго порядка дважды дифференцируемой функции равны. Пример 21. Найти частные производные второго порядка.
Дифференцирование неявной функции. Определение. Функция
Пример 22. Найти производные данных функций.
Локальный экстремум функции нескольких переменных. Определение 1. Функция Определение 2. Функция Необходимое условие экстремума. Если функция Точки, в которых частные производные обращаются в нуль или не существуют, называются критическими. Достаточный признак экстремума. Пусть функция Тогда 1) 2) 3)
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.119.34 (0.005 с.) |

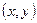 из некоторого множества по какому-либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.
из некоторого множества по какому-либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.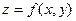 представляет собой некоторое множество точек на координатной плоскости Oxy. Координата z называется аппликатой, и тогда сама функция изображается в виде некоторой поверхности в пространстве E3. Например:
представляет собой некоторое множество точек на координатной плоскости Oxy. Координата z называется аппликатой, и тогда сама функция изображается в виде некоторой поверхности в пространстве E3. Например:
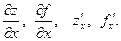
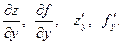
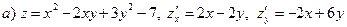
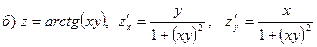
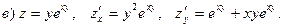
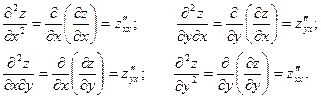

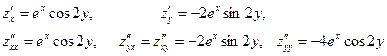
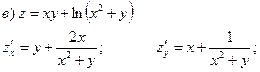
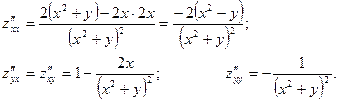
 называется неявной, если она задается уравнением
называется неявной, если она задается уравнением 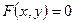 , не разрешимым относительно y. Производная такой функции находится по формуле:
, не разрешимым относительно y. Производная такой функции находится по формуле: .
.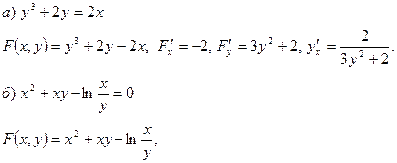
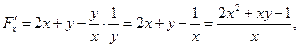
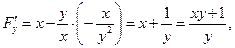
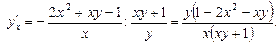
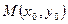 , если
, если 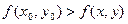 для всех точек
для всех точек 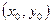 и отличных от нее.
и отличных от нее.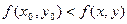 для всех точек
для всех точек 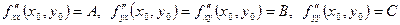
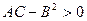 и
и 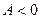 ;
;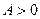 ;
; ;
;


