
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как решаются дифференциальные уравнения первого порядка с разделяющимися переменными?Содержание книги
Поиск на нашем сайте
Каким методом решаются линейные дифференциальные уравнения первого порядка?
Тема 8. Р я д ы Литература: 1. Шипачев В.С. Высшая математика. М. Высшая школа. 2008. Гл. 14. 2. Красс М.С. Математика для экономических специальностей. М. Дело. 2002. Гл. 8. Методические указания
Числовым рядом или просто рядом называется выражение вида
Числа Примером бесконечного ряда, например, является гармонический ряд
n -й член которого Если все члены ряда неотрицательны, то такой ряд называется положительным. Также существуют так называемые знакочередующиеся ряды, имеющие вид
Ряд вида
расположенный по возрастающим целым неотрицательным степеням переменной х и имеющий коэффициенты
Суммы конечного числа членов ряда называются частичными суммами:
Ряд называется сходящимся, если при неограниченном возрастании числа членов ряда n, существует конечный предел последовательности его частичных сумм – этот предел называется суммой ряда S.
В противном случае ряд называют расходящимся. Бесконечный расходящейся ряд суммы не имеет. При исследовании рядов на сходимость используют так называемые признаки сходимости. Для положительных рядов наиболее широко применяют признак Даламбера. Признак сходимости Даламбера. Если все члены ряда положительны и при неограниченном возрастании номера n члена ряда, существует предел отношения последующего члена ряда к предыдущему равный l, то есть
тогда, если: 1. 2. 3.
Признак сходимости Лейбница обычно используют при исследовании на сходимость знакочередующихся рядов. Если модули членов знакочередующегося ряда монотонно убывают при возрастании их номера, то есть
то ряд сходится. Для любого степенного ряда существует конечное и или бесконечное неотрицательное число R – радиус сходимости ряда – такое, что если
Рассмотрим несколько примеров исследования рядов на сходимость. Задача 25. Дан ряд
Решение. Очевидно, формула общего члена данного ряда будет иметь вид
Для исследования знакочередующегося ряда на сходимость используем признак Лейбница. Вначале проверим монотонность убывания модуля члена ряда при увеличении его номера
Первое условие признака Лейбница выполняется. Проверим второе условие
Это условие также выполняется. Следовательно, данный ряд сходится.
Задача 26. Написать первые три члена ряда
Решение. Для получения трех первых членов ряда берем последовательно n = 1, 2, 3,…, запишем данный ряд в виде:
Для нахождения области сходимости ряда применим признак Даламбера:
=
=
Данный ряд сходится абсолютно при значениях х, которые удовлетворяют неравенству:
Теперь исследуем сходимость ряда на концах полученного интервала. При
Полученный ряд является знакочередующимся. Члены ряда убывают по абсолютной величине, а также абсолютная величина его общего члена стремится к нулю при n → ∞. Следовательно, по признаку Лейбница такой ряд сходится и значит, При
Так как несобственный интеграл сходится, то сходится и соответствующий ряд. Значит, при Таким образом, область сходимости ряда:
Вопросы для самопроверки
1. Сформулируйте определение числового ряда. 2. Какой числовой ряд называется сходящимся?
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 172; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.119.149 (0.009 с.) |

 .
.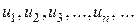 называются членами ряда, член с произвольным номером
называются членами ряда, член с произвольным номером 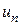 – общим членом ряда.
– общим членом ряда. ,
,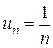 .
. ,
,  ,
,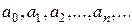 не зависящие от х, называется степенным рядом.
не зависящие от х, называется степенным рядом.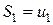 ,
, 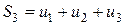 ,
,  .
.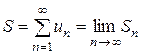 .
.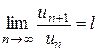 ,
,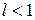 – ряд сходится.
– ряд сходится.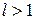 – ряд расходится
– ряд расходится – признак определенного ответа о сходимости или расходимости ряда не дает, требуется дополнительное исследование.
– признак определенного ответа о сходимости или расходимости ряда не дает, требуется дополнительное исследование.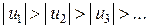 , и n -й член ряда при неограниченном возрастании n стремится к нулю
, и n -й член ряда при неограниченном возрастании n стремится к нулю ,
, , то при
, то при  , ряд сходится, а при
, ряд сходится, а при  – расходится. При
– расходится. При  может иметь место как сходимость, так и расходимость степенного ряда. Интервал
может иметь место как сходимость, так и расходимость степенного ряда. Интервал  называется интервалом сходимости степенного ряда. В случае, если
называется интервалом сходимости степенного ряда. В случае, если 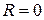 , степенной ряд сходится лишь в точке х = 0, и интервал сходимости не существует.
, степенной ряд сходится лишь в точке х = 0, и интервал сходимости не существует. . Написать формулу общего члена ряд и исследовать его на сходимость.
. Написать формулу общего члена ряд и исследовать его на сходимость. .
. .
.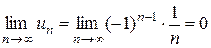 .
.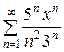 . Найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
. Найти интервал сходимости ряда и исследовать его сходимость на концах интервала.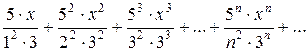 , или
, или ..
..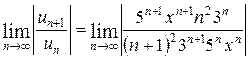 =
=  =
= 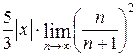 =
=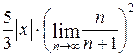 =
=  =
=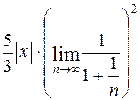 =
=  =
=  =
=  =
= 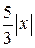 .
.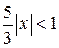 или
или 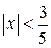 , то есть
, то есть  .
.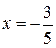 , данный ряд принимает вид:
, данный ряд принимает вид: =
= 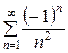 .
.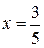 , ряд принимает вид
, ряд принимает вид 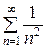 . Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
. Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл: =
= 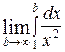 =
=  =
= 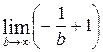 = 0 + 1 = 1.
= 0 + 1 = 1.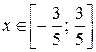 .
.


