
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии оценивания контрольной работыСодержание книги
Поиск на нашем сайте
Количество баллов за контрольную работу равно проценту правильно решенных задач или их частей. За каждую задачу контрольных работ можно получить максимум 17 первичных баллов. При наличии промежуточных ошибок, но с последующей правильной логикой решения, или при арифметической погрешности задача считается решенной частично правильно. При этом балл за задачу снижается на 3,5 балла за каждую промежуточную негрубую логическую ошибку и на 2,5 балла – за каждую арифметическую погрешность, не приводящую к алогичным выводам. За отсутствие ответа к задаче за нее снижается 2 балла. + 2 балла за задачу при грамотном, логически последовательном оформлении хода решения с наличием ответа к каждой задаче, четкие выводы. + 5 баллов за аккуратное структурированное оформление всей работы. Работа считается зачтенной, если за нее получено не менее 60 баллов. В противном случае работа возвращается студенту на доработку. Незначительные ошибки можно исправить во время аудиторных занятий. КОНТРОЛЬНЫЕ ЗАДАНИЯ 1. Даны матрицы А, В, С. Вычислить матрицу D=AB+C
Вычислить определитель третьего порядка
Решить систему линейных уравнений 1. 4. 7. 10.
Составить уравнение прямой линии на плоскости, проходящей через заданные точки 1. (–1, 2) и (0, 10); 2. (–2, –1) и (3, 9); 3. (–3, 1) и (4, 8); 4. (–4, 3) и (–2, 7). 5. (–5, 2) и (0, 6); 6. (–6, –1) и (3, 5); 7. (–7, 1) и (4, 4); 8. (–8, 3) и (–2, 3). 9. (–9, 2) и (0, 2); 10. (–10, –1) и (3, 1).
5. Построить график функции (с помощью преобразования графиков основных элементарных функций) 1. 5. 9.
Значение функции f(x) известно в точках а и b. С помощью линейной интерполяции найти значение функции в точке с
Задача межотраслевого баланса. Модель Леонтьева.
В таблице приведены данные об исполнении баланса за отчетный период, у.е. Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление первой отрасли увеличится вдвое, а второй – на 20%.
Где k – номер варианта контрольной работы.
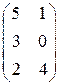
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ 1.1. Сложить две матрицы Решение. Складывать (вычитать) можно только матрицы одинакового размера, а т.к. размеры матрицы А – (3´2) и В – (3´2) (где 3 – число строк, 2 – число столбцов) совпадают, то для того, чтобы сложить две матрицы, надо к каждому элементу первой матрицы прибавить соответствующие элементы второй матрицы:
Ответ:
1.2. Умножить матрицу Решение. Для того, чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число:
Ответ:
1.3. Умножить матрицу Решение. Умножение матриц А и В определено, если число столбцов первой матрицы равно числу строк второй.
Совпадают
Размерность результирующей матрицы
В нашем случае размер А – (2´3), а размер В – (3´3), поэтому умножение производить можно; размерность результирующей матрицы С – (2´3). Для того чтобы получить элемент, стоящий на пересечении i –й строки и j –го столбца новой матрицы, нужно элементы i –й строки первой матрицы умножить на соответствующие элементы j –го столбца второй матрицы и результат сложить, т.е. элементы матрицы С вычисляются по формуле:
C= = Ответ: C=
2. Вычислить определитель 3-го порядка: Решение. 1) Метод разложения по элементам строки или столбца. С помощью метода разложения по элементам строки (столбца) можно вычислить определители любого порядка. Строку (столбец), по элементам которого производится разложение, следует выбирать так, чтобы в ней содержалось наибольшее количество нулей. Разложим определитель по элементам какой-либо строки или столбца. Например, выберем для разложения третий столбец:
Здесь А13, А23, А33 – алгебраические дополнения элементов матрицы а13, а23, а33 соответственно, которые в общем случае для элемента аij находятся по формуле
Аij = (–1) i+j∙Mij. (2) Минор Мij – определитель, получаемый из исходного вычеркиванием i ‑й строки и j ‑го столбца, на пересечении которых стоит данный элемент. Например, для нахождения М13 вычеркивается 1-я строка и 3-йстолбец:
Аналогично определяем М23, вычеркивая 2-ю строку и 3-й столбец. М33 получается вычеркиванием 3-й строки и 3-го столбца:
Тогда алгебраические дополнения (по формуле (2)) будут равны: А13 = (–1)1+3 ∙M 13= (–1)4∙6 = 6, А33 = (–1)3+3 ∙M 33=(–1)6∙3 = 3. Подставляя найденные значения в (1), найдем определитель
Ответ: 27.
2) Метод Саррюса. С помощью метода Саррюса можно вычислять только определители третьего порядка. Сначала к исходному определителю справа приписываем первый и второй столбцы:
Тогда определитель равен сумме произведений элементов, стоящих на главной диагонали и диагоналях, параллельных ей, взятых со своими знаками, и произведению элементов побочной диагонали и параллельных ей диагоналях, взятых с противоположными знаками.
Ответ: 27.
3. Решить систему линейных уравнений:
1) Метод Крамера. Выпишем определитель матрицы системы А: Δ = (Так как определитель не равен 0, то метод Крамера использовать можно, и система имеет единственное решение.) Определитель Δ1 получаем из определителя Δ заменой первого столбца на столбец свободных членов В, а остальные столбцы остаются прежними: Δ1 = Аналогично, заменяя в исходном определителе второй, а затем третий столбцы на столбец свободных членов, получим соответственно Δ2 и Δ3. Δ2 = Теперь воспользуемся формулой Крамера и найдем все переменные:
2) Метод Гаусса. Метод Гаусса – это универсальный метод решения систем линейных уравнений. Он заключается в последовательном исключении переменных. Составим расширенную матрицу системы, которая включает в себя матрицу системы и столбец свободных членов.
Произведем элементарные преобразования со строками матрицы, приведя ее к треугольному виду, т.е. к матрице, в которой все элементы, ниже главной диагонали равны нулю (при этом диагональные элементы не равны нулю). Шаг 1. Если в матрице элемент а 11 = 0, то перестановкой строк нужно добиться того, чтобы элемент а 11≠ 0. В нашем примере а 11≠ 0. Сначала обнулим элементы первого столбца ниже главной диагонали. Для этого поочередно умножим элементы первой строки на числа 2∙ -3
Шаг 2. Если в полученной матрице а 22 ≠ 0, то обнулим элемент второго столбца ниже главной диагонали. Для этого умножим вторую строку на число
Полученная матрица имеет треугольный вид. Т.о. получили систему уравнений:
Откуда найдем из последнего уравнения х 3 = 3; из второго х 2 = Ответ: х 1 = 1, х 2 = 2, х 3 = 3.
4. Составить уравнение прямой, проходящей через точки: А (5; 4) и В (2; –3). Решение. Уравнение прямой, проходящей через две точки М1(х1;y1) и М2(х2;y2) имеет вид: Уравнение прямой, проходящей через заданные точки:
Ответ: уравнение прямой
5. Построить график функции у = –4∙sin2 x + 1 (с помощью преобразования графиков основных элементарных функций).
1) Сначала построим график функции у = sin x. у
2) Сжатием графика в 2 раза вдоль оси Ох получаем график функции у =sin2 x.
3) Растянем график у = sin2 x вдоль оси Оу в 4 раза и получим график функции у = 4sin2 x. у
-4
4) Зеркально отобразив график относительно оси Ох, получим у = –4sin2 x. у
-4
5) Сдвинем полученный график на 1 единицу вверх параллельно оси Оу. Таким образом, график функции у = – 4∙sin2 x + 1 имеет вид: у
-3
6. Значение функции известно в точках a и b. С помощью линейной интерполяции найти значение функции в точке с.
Решение. Формула линейного интерполирования: f(c)» f(a) + Подставляя в формулу известные значения из таблицы, получим: f(2,008)» 2,42 + Ответ. f(2,008)» 2,512. 7. В таблице приведены данные (в ден. ед.) об исполнении баланса между двумя отраслями за некоторый период времени: Таблица
Вычислить: 1) Величину конечного продукта, если валовой выпуск составил бы
Необходимый объем валового выпуска отраслей, если объем конечного потребления увеличить до уровня ◄ Используя данные таблицы и формулу (6.5), получим матрицу прямых затрат 1) Вектор конечного продукта находим по формуле (6.8):
2) Вычисляем определитель как он оказался отличным от нуля делаем вывод, что матрица Все элементы полученной обратной матрицы оказались неотрицательными и, следовательно, в соответствие с приведенной выше теоремой матрица А продуктивна и решение уравнения (6.8) положительно при любых значениях конечного продукта, в частности, и при
Таким образом, чтобы обеспечить конечный продукт в объеме
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.95.129 (0.011 с.) |

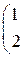
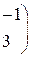
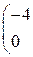

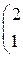
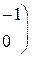
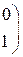
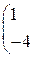
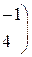

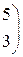
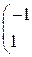
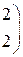
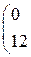



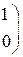
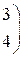
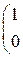

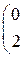
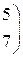
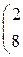

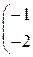
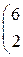
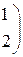

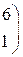

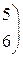
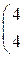
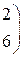

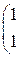

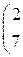
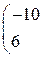
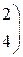
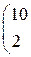
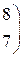
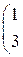
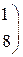
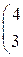
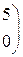
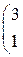
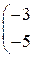

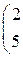
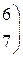
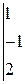
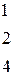
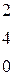
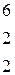

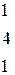
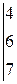

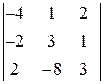

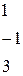
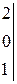
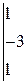
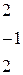
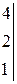
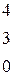

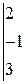
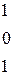

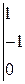

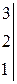 .
.
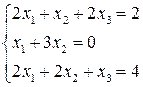 2.
2. 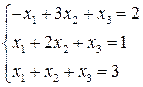 3.
3. 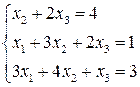
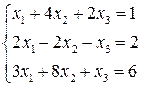 5.
5.  6.
6. 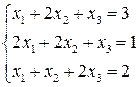
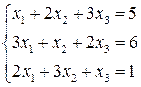 8.
8.  9.
9. 
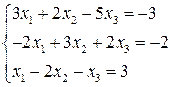
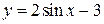 2.
2. 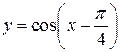 3.
3. 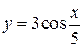 , 4.
, 4. 
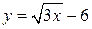 6.
6. 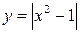 , 7.
, 7. 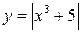 8.
8. 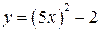 ,
,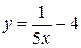 10.
10. 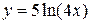
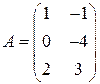 и
и 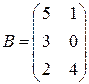
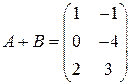 +
+  =
= 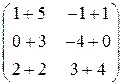 =
= 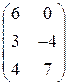 .
.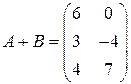 .
.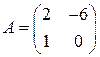 на число 3.
на число 3.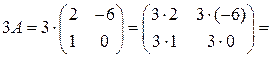
 .
.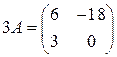 .
.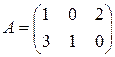 на матрицу
на матрицу 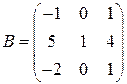 .
.

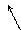
 С m´n = A m ´ k ∙ B k ´ n
С m´n = A m ´ k ∙ B k ´ n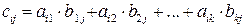 .
. ∙
∙ 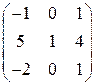 =
= 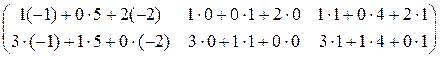
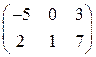 .
.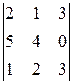 .
.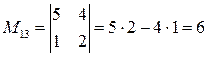 .
.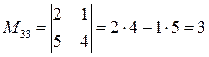 .
.

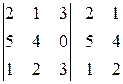 = 2∙4∙3 + 1∙0∙1 + 3∙5∙2 – 3∙4∙1 – 2∙0∙2 – 1∙5∙3 = 27.
= 2∙4∙3 + 1∙0∙1 + 3∙5∙2 – 3∙4∙1 – 2∙0∙2 – 1∙5∙3 = 27.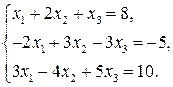
 = 4.
= 4. = 4.
= 4.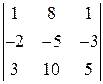 = 8, Δ3 =
= 8, Δ3 = 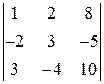 =12.
=12.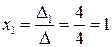 ,
,  ,
, 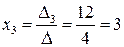 .
.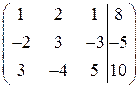 .
. и
и 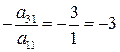 , и прибавим соответственно к элементам второй и третьей строк:
, и прибавим соответственно к элементам второй и третьей строк: +
+ 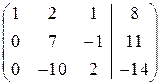
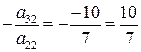 и прибавим к третьей строке:
и прибавим к третьей строке: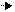

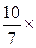
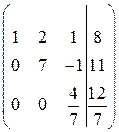 .
.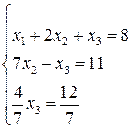
 =2; из первого х 1 = 8 – 2 х 2 – х 3 = 1.
=2; из первого х 1 = 8 – 2 х 2 – х 3 = 1.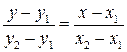 .
.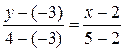
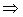
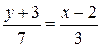
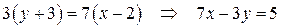 .
.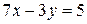
 Решение.
Решение.

 1
1
 О х
О х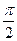 -1
-1 



 4
4










 , где h = b – a, Df = f(b) – f(a).
, где h = b – a, Df = f(b) – f(a).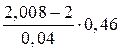 = 2,512.
= 2,512.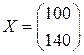 ;
;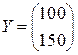 .
.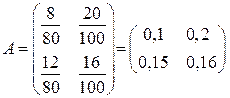 , а затем матрицу полных затрат
, а затем матрицу полных затрат 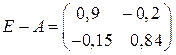 .
.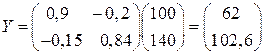 .
.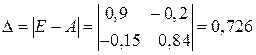 . Так
. Так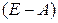 невырожденная и имеет обратную. Находим эту обратную матрицу:
невырожденная и имеет обратную. Находим эту обратную матрицу: 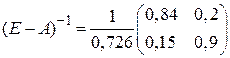 .
.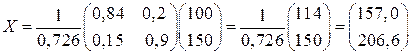 .
.



