Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Никаких других формул в логике высказываний нет.Содержание книги
Поиск на нашем сайте Определение такого вида называется индуктивным. В п.п. 1 и 2 определены элементарные формулы, в п.п. 3 и 4 даны правила образования новых формул из любых двух данных формул. Условимся для упрощения записей не заключать в скобки формулы, не являющиеся частями других формул или стоящие под знаком отрицания. Заметим, что в формуле число левых скобок всегда должно быть равно числу правых скобок. Опишем процедуру формализации высказываний: 1. Если высказывание – простое, то ему ставится в соответствие элементарная формула. 2. Если высказывание – составное, то для составления соответствующей формулы нужно: а) выделить все элементарные высказывания и логические связки, образующие данное составное высказывание; б) заменить их соответствующими символами; в) расставить скобки в соответствии со смыслом данного высказывания. Пример 8: Определите логическую структуру высказываний (формализуйте высказывания): 1. Е = «Ваш приезд не является ни необходимым, ни желательным». Составляющие простые высказывания: А = Ваш приезд необходим; В = Ваш приезд желателен. Они соединены между собой неявно имеющимся в высказывании Е союзом «и» и, кроме того, к каждому из них относится частица «не». Таким образом, форма сложного высказывания имеет вид: 2. Е = «Поиски врага длились уже три часа, но результатов не было, притаившийся враг ничем себя не выдал». Переформулируем высказывание таким образом, чтобы выделить логические связки, неявно соединяющие простые высказывания: «Если притаившийся враг ничем себя не выдал, то его поиски длились уже три часа и результатов не было». Теперь можно выделить простые высказывания: А = Враг себя выдал; В = Поиски врага длились уже три часа и С = Результат был. Теперь можно формализовать сложное высказывание: Замечание: Символ импликации ставится там, где подразумевается вторая часть союза «если…, то…», т.е. на месте «то». Таким образом, формула, полученная во втором примере, читается: «Если не А, то В и не С». 3. Е = «Если число делится на 2 и на 3, то оно делится на 6». В этом высказывании можно выделить следующие элементарные высказывания: А = Число делится на 2, В = Число делится на 3 и С = Число делится на 6. Тогда формула, соответствующая сложному высказыванию, имеет вид: Последний пример наглядно показывает, почему математическую логику интересует только логическая структура высказываний. Точно такую же логическую структуру, как в третьем примере имеет большое количество, например, математических теорем: «Если в четырехугольнике противоположные стороны параллельны и равны, то этот четырехугольник - параллелограмм» или «Если две прямые параллельны третьей прямой, то они параллельны друг другу». Пример 9: По форме высказываний и выраженным на естественном языке составляющим его простым высказываниям получить фразу на естественном языке. 1. Составляющие простые высказывания: А = Человек с детства давал нервам властвовать над собой. В = Человек в юности давал нервам властвовать над собой. С = Нервы привыкнут раздражаться. D = Нервы будут послушны. Для начала прочитаем формулу с использованием логических связок, не обращая внимания на смысл составляющих простых высказываний: «Если не А и не В, то не С и D». Теперь подставим вместо букв соответствующие высказывания, не произнося повторяющиеся части или заменяя их синонимами (местоимениями). Получим следующую фразу на естественном языке: Е = Если человек с детства и юности своей не давал нервам властвовать над собой, то они не привыкнут раздражаться и будут ему послушны. (К.Д. Ушинский) 2. Составляющие простые высказывания: А = Некто является врачом. В = Больной поговорил с врачом. С = Больному стало легче. Фраза на естественном языке: Е = Если больному после разговора с врачом не становится легче, то это не врач. (В.М. Бехтерев) Вычислить значение логического выражения (формулы ЛВ) – значит найти значение истинности этого выражения при заданных значениях истинности составляющих переменных. При вычислении значения формулы ЛВ логические операции (если нет скобок) вычисляются в определенном порядке: 1) негация (отрицание); 2) конъюнкция; 3) дизъюнкция; 4) импликация и 5) эквиваленция. Пример 10: Даны формулы. Определить порядок вычисления формул: 1. 1) отрицание 2. 1) отрицание Удобной формой записи при нахождении значений формулы, соответствующих всевозможным наборам значений ее переменных, является таблица, которую называют таблицей истинности. Для начала научимся определять количество строк в таблице. Если высказывание одно, то оно может принимать только два значения истинности – «истина» и «ложь», поэтому строк в такой таблице 3 (две строки для значений переменной и строка заголовка). Примером такой таблицы служит таблица истинности в определении негации. Если переменных в формуле две, то они могут принимать одновременно такие значения: оба высказывания истинны, первое – истинно, а второе – ложно, первое – ложно, а второе – истинно и, наконец, оба они могут быть ложными. Число строк в такой таблице равно 5 (плюс строка заголовка). Вообще, число наборов значений, которые могут принимать п переменных, находится как 2п. Сформулируем алгоритм построения таблицы истинности сложного высказывания: 1. Вычислить количество строк и столбцов в таблице истинности. Пусть в формуле п различных переменных и k операций. Переменные считаем каждую только один раз, а символы операций – все, сколько есть. Тогда число строк в таблице равно 2п + 1 (число наборов значений переменных плюс строка заголовка), а число столбцов в таблице равно n + k. 2. Начертить таблицу. 3. Заполнить строку заголовка. В строке заголовка записываем промежуточные формулы, начиная с элементарных и учитывая порядок выполнения операций. Вместо промежуточных формул, если они большие, можно записывать их порядковые номера (из порядка выполнения операций). 4. Заполнить оставшиеся строки таблицы, начиная с первого столбца. При вычислении значений промежуточных формул, надо помнить, что в каждой операции участвует не более двух формул (может быть и не элементарных). Пример 11: Составить таблицы истинности для формул: 1) 1. Определим порядок выполнения операций: 1) отрицание Заполняем строку заголовка, начиная с элементарных формул:
По-другому строка заголовка может выглядеть так:
Заполняем первый столбик значениями истинности переменной К, для этого число пустых строк делим пополам (4: 2 = 2) и в половине пишем значение «истина», а в оставшейся половине – «ложь»:
Заполняем второй столбик значениями истинности переменной С. Для этого число пустых строк делим на 4 (4: 4 = 1) и попеременно записываем в строки по одному значению «истина» и «ложь» таким образом, чтобы каждому значению истинности переменной К соответствовали оба значения истинности переменной С:
Начиная с третьего столбика, заполняем строки результатами выполнения операций. В третьем столбике записываем результат выполнения операции отрицания
В четвертом столбике записываем результаты выполнения дизъюнкции
В пятом столбике записываем результаты выполнения операции конъюнкции
И, наконец, в шестом столбике записываем результаты выполнения итоговой операции импликации
Из итогового результата мы можем сделать следующий вывод: какие бы по смыслу элементарные высказывания не составляли высказывание, соответствующее данной логической структуре, в итоге мы получим истинное высказывание.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |


 .
. .
. .
. .
.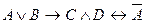 . Порядок вычисления следующий:
. Порядок вычисления следующий: ; 2) конъюнкция
; 2) конъюнкция  ; 3) дизъюнкция
; 3) дизъюнкция  ; 4) импликация
; 4) импликация 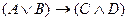 и, наконец, эквиваленция
и, наконец, эквиваленция  .
. . Порядок вычисления следующий:
. Порядок вычисления следующий: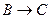 ; 3) конъюнкция
; 3) конъюнкция  ; 4) дизъюнкция
; 4) дизъюнкция  ; и 5) эквиваленция
; и 5) эквиваленция  .
. ; 2)
; 2)  .
. ; 2) дизъюнкция
; 2) дизъюнкция 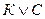 ; 3) конъюнкция
; 3) конъюнкция  и 4) импликация
и 4) импликация  .
.