
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Импликацией двух высказываний называется новое высказывание, которое ложно тогда и только тогда, когда первое высказывание истинно, А второе – ложно.Содержание книги
Поиск на нашем сайте
Импликация обозначается Таблица истинности импликации выглядит так:
Пример 6: Чтобы запомнить правило нахождения значения истинности импликации, удобно воспользоваться следующими высказываниями: «Дождь идет», «Асфальт мокрый», «Дождь не идет», «Асфальт сухой». 1) 2) 3) 4) Принятое определение импликации соответствует употреблению союза «если…, то…» не только в математике, но и в обыденной, повседневной речи. Так, например, обращение приятеля «Если будет хорошая погода, то я приду к тебе в гости» вы расцените как ложь в том и только в том случае, если погода будет хорошая, а приятель к вам в гости не придет. Вместе с тем определение импликации вынуждает считать истинными высказываниями такие предложения, как «Если 2×2 = 4, то Москва – столица России» или «Если 2×2 = 5, то существуют ведьмы». Эти предложения, вероятно, кажутся бессмысленными. Дело в том, что мы привыкли соединять союзом «если…, то…» (так же, как и другими союзами) предложения, связанные по смыслу. Но определениями логических операций смысл составляющих высказываний никак не учитывается; они рассматриваются как объекты, обладающие единственным свойством – быть истинными либо ложными. Поэтому не стоит смущаться «бессмысленностью» некоторых составных высказываний, их смысл не входит в предмет нашего рассмотрения. 5. Эквиваленция (логическая равносильность). Эквиваленцией двух высказываний называется новое высказывание, которое истинно тогда и только тогда, когда оба высказывания одновременно истинны либо ложны. Эквиваленция обозначается Таблица истинности для эквиваленции выглядит так:
В форме эквиваленции, как правило, формулируются определения (например, определения логических операций). Пример 7: Пусть через А обозначено высказывание «9 делится на 3», а через В – высказывание «10 делится на 3». Составьте высказывания, имеющие логическую структуру: а)
Решение. а) Формулы логики высказываний В логике высказываний – первом и основном разделе математической логики – элементарные высказывания рассматриваются как нерасчленяемые «атомы», а составные высказывания – как молекулы, образованные из «атомов» применением к ним логических операций. Логика высказываний интересуется единственным свойством элементарных высказываний – их значением истинности; составные же высказывания изучаются ею со стороны их логической структуры, отражающей способ, которым они образованы. Структура составных высказываний определяет зависимость их значений истинности от значений истинности составляющих элементарных высказываний. Так как смысл высказываний математическую логику не интересует, их вполне можно заменить переменными. Пусть X, Y,…, Z,…, Xi, Yi,…, Zi – переменные, вместо которых можно подставить любые элементарные высказывания (или их значения истинности). Такие переменные называют пропозициональными или высказывательными переменными. С помощью высказывательных переменных и символов логических операций любое высказывание можно формализовать, т.е. заменить формулой, отражающей его логическую структуру. Начнем с того, что уточним понятие формулы логики высказываний. Для этого зададим алфавит, т.е. набор символов, которые мы будем употреблять в логике высказываний: 1) Х, Y,…, Z,…, Xi, Yi,…, Zi (i – натуральное число) – символы для обозначения высказывательных переменных; 2) И, Л, 1, 0 – символы, обозначающие логические константы «истина» и «ложь»; 3) 4) (,), [, ] – скобки (вспомогательные символы, служащие для указания порядка выполнения операций).
Дадим теперь строгое определение формулы логики высказываний (будем говорить формула ЛВ):
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.162.166 (0.009 с.) |

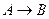 или
или  , читается «Если А, то В».
, читается «Если А, то В».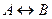 или
или  , читается «А тогда и только тогда, когда В».
, читается «А тогда и только тогда, когда В». ; в)
; в)  ; д)
; д)  ; е)
; е)  и определите их значения истинности.
и определите их значения истинности. = 0 и В = 0, следовательно,
= 0 и В = 0, следовательно,  = 1, тогда
= 1, тогда  – символы логических операций;
– символы логических операций;


