
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Результаты экспериментальных исследований грядообразователя фрезерного типаСодержание книги
Поиск на нашем сайте При полевых испытаниях рабочих органов экспериментальных машин, критериями оценки, отражающих качество обработки, выбраны снижение энергозатрат и степень крошения почвы. При этом необходимо отметить, что обеспечение заданного режима вращения (вращения без проскальзывания и торможения) почвообрабатывающих рабочих органов ротационного типа, является технологическим показателем, в значительной мере, определяющим агротехническое качество обработки почвы [4, 92, 112, 148]. Тягово-приводной агрегат для предпосадочной подготовки почвы под картофель (рис.4.8) одновременно выполняет две технологические операции: рыхление и измельчение почвы рабочими органами активного действия; формирование гряды (гребня).
Рисунок 4.8. – Рабочие органы грядообразователя фрезерного типа (Патент) Для определения рациональных конструктивно-технологических параметров и режимов работы ротационных рабочих органов активного действия проведены экспериментальные исследования с использованием методов планирования экспериментов [2, 27, 28, 36, 87, 94, 192, 193]. Основной задачей планирования экспериментов являлось нахождение математической зависимости параметров оптимизации технологического процесса от влияния каждого из исследуемых факторов или их совокупного влияния на процесс. Таблица 4.3 - Уровни и интервалы варьирования факторов
Для получения математической модели процесса использован композиционный план Хартли второго порядка, который состоит из полуреплики полного факторного эксперимента типа 24-1 и опытов в звездных точках и центре плана. Определяющий контраст плана:
Интервал варьирования фактором X1 (скорость поступательного движения агрегата), интервал варьирования фактором X2 (число ножей рабочего органа), интервал варьирования фактором Х3 (длина пальцев) выбран на основании предварительных расчетов глава 3. Интервал варьирования фактором Х4 (угол наклона диска ротора) выбран по рекомендациям работ [4, 39]. Кодовое обозначение, интервалы и уровни варьирования факторами приведены в табл. 4.3. Матрица плана эксперимента в раскодированном виде приведена в табл. 4.4. Многофакторный эксперимент, обработка результатов эксперимента и их проверка были проведены в соответствии с общепринятыми методами. Таблица 4.4 - Матрица плана эксперимента в раскодированном виде
Дисперсия параметра оптимизации в каждой строке матрицы определялась по формуле:
где: Проверка воспроизводимости эксперимента производилась с помощью критерия Кохрена:
где: Полученное в результате расчетов значение критерия Кохрена ( Эксперимент воспроизводим при значениях критерия Кохрена Gрасч < Gтабл. Дисперсии параметра оптимизации усреднялись и для расчетов пользовалась средняя дисперсия опыта:
Коэффициенты уравнения регрессии вычислялись по формулам[ ]:
Коэффициенты факторов, входящих в определяющий контраст рассчитывают по формуле (4.16). Для проверки статистической значимости коэффициентов находим дисперсии ошибок определения коэффициентов регрессии, ковариации и среднеквадратическое отклонение дисперсии ошибок /60/:
Значимость коэффициентов регрессии определяли no t - критерию Стьюдента. Табличное значение t-критерия (tкр) принималось при числе степеней свободы
Проверка адекватности математической модели экспериментальным данным осуществлялась по критерию Фишера (Fрасч):
где:
где: Модель объекта исследования второго порядка имеет вид:
Для подтверждения гипотезы об адекватности модели определялось табличное значение критерия Фишера (Fтабл) при уровне значимости g=5% и число степеней свободы V1=m-1 и V2=N. При условии Fрасч<Fтабл гипотеза об адекватности модели подтверждается: уравнение не противоречит экспериментальным данным и достоверно описывает исследуемый процесс. Уравнение (4.21) используется для построения поверхности отклика (рис.4.9, рис.4.10) изменения структурного состояния почвы в зависимости от изменения кинематических параметров режимов работы. С целью определения экстремума функции рассмотрим поверхность отклика в трехмерном пространстве при фиксированных граничных значениях влажности удобрений в области эксперимента.
Рисунок 4.9 – Однородность фракционного состава от кинематического параметра и глубины обработки, при D = 0,5м, n = 24
а = 0,14, n = 24 Рисунок 4.10 – Однородность фракционного состава от изменения диаметра фрезбарабана и кинематического параметра, при n = 24, а =10см
Установлено, что значения однородности фракционного состава почвы соответствующие агротехническим до 90% находятся в области значений по глубине обработки - а=0,12-0,16м, по количеству ножей находящихся в одной плоскости - n=3-4шт. Диапазоны значений по глубине обработки и по обоснованию количества ножей совпадают с теоретическими значениями. Режимные характеристики тягово-приводного агрегата характеризуются кинематическим параметром фрезерного барабана, определяемый отношением окружной скорости к поступательной скорости агрегата. Установлено, что значения однородности фракционного состава почвы соответствующие агротехническим до 90% находятся в области значений по диаметру фрезерного барабана D=0,5м, по значениям кинематического параметра λ = 3-5. Диапазоны значений по глубине обработки и по обоснованию количества ножей совпадают с теоретическими значениями. Условия экстремума соответствует максимуму при влажности почвы 22%.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 472; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.01 с.) |


 (4.10)
(4.10) ; (4.11)
; (4.11)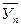 - среднеопытное значение параметра оптимизации;
- среднеопытное значение параметра оптимизации;  - значение параметра оптимизации i-ой повторности; m - число повторностей опыта.
- значение параметра оптимизации i-ой повторности; m - число повторностей опыта. (4.12)
(4.12) - наибольшая построчная дисперсия;
- наибольшая построчная дисперсия;  - расчетное значение критерия Кохрена;
- расчетное значение критерия Кохрена;  - сумма построчных дисперсий;
- сумма построчных дисперсий;  - число опытов эксперимента.
- число опытов эксперимента. ), принятым при уровне значимости g= 5 % и числе степеней свободы V1=m-1 и V2=N.
), принятым при уровне значимости g= 5 % и числе степеней свободы V1=m-1 и V2=N. ;
;  (4.13)
(4.13)
 (4.14)
(4.14)
 (4.15)
(4.15)
 (4.16)
(4.16)
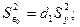




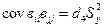 (4.17)
(4.17)
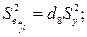

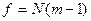 и уровне значимости g=5%. Коэффициенты уравнения регрессии считались значимыми, если выполнялось условие:
и уровне значимости g=5%. Коэффициенты уравнения регрессии считались значимыми, если выполнялось условие: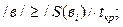 (4.18)
(4.18) (4.19)
(4.19) - дисперсия адекватности.
- дисперсия адекватности. (4.20)
(4.20) - экспериментальные и расчетные значения параметра; k - число факторов эксперимента.
- экспериментальные и расчетные значения параметра; k - число факторов эксперимента. (4.21)
(4.21)




