
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для вероятности безотказной работы будем иметьСодержание книги
Поиск на нашем сайте P = 1 – 0,1 = 0,9, Pн= 1 –qв= 0,977, Pв = 1 – qн = 1.0. Пример П.4.3. В результате обработки данных по надежности изделий функциональной системы самолетов, эксплуатирующихся по состоянию, были сформированы цензурированные данные 50 изделий. Наработки до отказа (n = 23): 2292, 5440, 880, 2996, 1711, 14610, 10806, 4652, 1638, 1287, 2850, 4830, 2700, 755, 3438, 581, 1904, 23289, 12036, 8550, 742, 1064, 2640 ч. Наработки до цензурирования (m = 27): 25 изделий были сняты с наблюдения при наработке 3600 ч., а два изделия при наработке 25000 ч. Для внедрения прогрессивного метода эксплуатации изделий на всем парке самолетов требуется оценить показатели надежности.
581, 742, 755, 880, 1064, 1287, 1638, 1711, 1904, 2292, 2640, 2700, 2850, 2996, 3438, 3600(25), 4652, 4830, 5440, 8550, 10806, 12036, 14610, 23289, 25000 (2). 2) По вариационному ряду (ранжированной временной диаграмме) определяем интервалы наблюдения (l = 2)
Для каждого интервала наблюдения определяем n1=15, m0=0, m2=2, n2=8, Nэ1 = N-n0 = 50, 3) Определяем значения эмпирической функции распределения F*(t) по (4.14) или (4.15). Таблица П. 4.1 Значения функции распределения F*(ti)
4) Определим точечные оценки вероятности безотказной работы за 5000, 10000 и 20000 ч. Заданные наработки:
Р*(5000) = 1- [diF*(ti) + (1 - di)F*(ti- 1)] = 1 - (О,279 • 0,51 + 0,721 • 0,43) = 0,55 t23=10000 ч,I=45, τi= 10806; τi-1 =8550;
P*(10000) = 1 - (0,567 • 0,65 + 0,433 • 0,58) = 0,38, t33= 20000 ч; I = 48; τi = 23289; τi-1 = 14610;
P*(20000) = 1 - (0,621 • 0,86 + 0,379 • 0,79) = 0,16. 5) Определим среднюю наработку до отказа
6) Вычисление 95% - й наработки до отказа показывает, что она лежит между вторым и третьим членами вариационного ряда (таб. П.4.1),
т.е. F*(ti) = 0,05, следовательно, i = 3; F*(ti-1) = 0,04; F*(ti) = 0,06; τ i-1 = 742 и τi = 755;
T* γ = (1 - d2) τ i. + d2 τ 1 = 0,5 • 742 + 0,5 • 755 = 748,5 ч.
7) Доверительный интервал для значений вероятностей безотказной работы P*(t3) оценим, задавшись доверительной вероятностью β = 0,95. t13 = 5000ч; I –1=42; I=43; l=2, во втором интервале: ν=23; ύ=25;
Для β=0,95 (односторонние доверительные границы) Ưβ=1,645;
Pн =P*(tз)-Ưβσİ=0,55 -1,645 0,08 = 0,42 PВ =P*(tз)+Ưβσİ=0,55 + 1,645 -0f08 • 0,68 . t3 =10000 ч, I-1=44, Ii=45, l=2
Pн =0,38 -1,645 0,06 =0,282; PВ =0,38 + 1,645 0,06 =0,478 , t3 =20000 ч, I-1=47, I=48, l=2
Рн = 0,16 - I, 645 0.02 =0,128, PВ =0,16 + 1,645• 0,02 - 0.I92,
Результаты оценки приведены на рис. П. 4.1.
Рис. П.4.2. Временная диаграмма однотипных восстанавливаемых изделий: N – число наблюдаемых объектов (N = N0k); N0- число самолетов, k – число однотипных изделий на самолете.
Рис. П.4.3. График P(t) для восстанавливаемых изделий. .
нет
нет да
Рис. П. 4.4. Алгоритм анализа надежности СКВ самолета и ее изделий на соответствие требованиям надежности при эксплуатации
ПРИЛОЖЕНИЕ 5 Таблицы характеристик распределения случайных величин
Таблица П. 5.1 Функция стандартного нормального распределения
Таблица П. 5.1 (продолжение) Значения
Таблица П.5.2 Плотность стандартного нормального распределения f(x)
Таблица П. 5.3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |


 1) Строим вариационный ряд или ранжированную временную диаграмму наработок до отказа τi, i = 1,…,n и цензурирования tj, j = 1,…,m
1) Строим вариационный ряд или ранжированную временную диаграмму наработок до отказа τi, i = 1,…,n и цензурирования tj, j = 1,…,m (0,τ15) (0;3438),
(0,τ15) (0;3438), (τ16,τ23) (3438;23289).
(τ16,τ23) (3438;23289).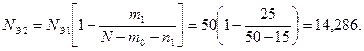 .
.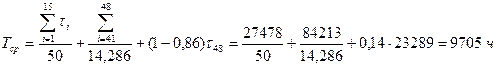
 σi= [1-0,43] √ 18/(25· 27)= 0,57 · 0,I4=0.08,
σi= [1-0,43] √ 18/(25· 27)= 0,57 · 0,I4=0.08, σi= [1-0,58] √ 20/25 27= 0.06,
σi= [1-0,58] √ 20/25 27= 0.06, σi= [1-0,86] √ 23/25· 27= 0.02,
σi= [1-0,86] √ 23/25· 27= 0.02,












 нет
нет



 нет
нет








