Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение уровня процентной ставкиСодержание книги Поиск на нашем сайте
Это бывает необходимо при сравнении контрактов по степени доходности в случае, когда проценты в явном виде не указаны. Решив уравнения наращения относительно i и d, получим: Процентная ставка:
Учетная ставка: где k – временная база
Формула для расчета наращенной суммы для учетной ставки:
В мировой практике выделяют и такие 2 концепции начисления процентов:
I. Дискурсивный способ (последующий) Проценты начисляются в конце каждого интервала начисления, их величина определяется, исходя из величины предоставляемого капитала. Соответственно дискурсивная процентная ставка или ссудный процент представляет собой выраженное в процентах отношение суммы начисленного капитала за определенный интервал дохода к сумме, имеющейся на начало данного интервала. II. Антисипативный способ (предварительный) Проценты начисляются в начале каждого интервала начисления. Сумма процентных денег определяется исходя из наращенной суммы. Процентная ставка будет выражена как процент отношения суммы дохода, выплачиваемого за определенный интервал к величине наращенной суммы, полученной по прошествии этого интервала. Полученная т.о. ставка процента соответствует учетной, наз. в широкой практике антисипативной.
Сложная процентная ставка
Если проценты не выплачиваются сразу после их начисления, а присоединяются к основной сумме долга, то говорят об использовании концепции сложного процента (когда база для наращения увеличивается с каждым шагом во времени). Начисление и присоединение процента представляет собой наращение. Присоединение процента к сумме, которая служила базой для их расчета наз. капитализацией процента. Она может иметь место 1 раз в год, 2, 4, 12/365 и чаще.
Формула для расчета наращенной суммы по сложным процентам имеет вид:
где i – годовая ставка процента P – первоначальная величина (база) n – число периодов (лет) (Проценты капитализируются один раз в год)
Получили данную ф., описывая геометрическую прогрессию:
* Примечание:
Рассчитанные по разным ф. величины наращенной суммы будут несколько отличаться друг от друга
|
||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

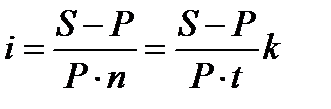
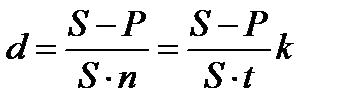
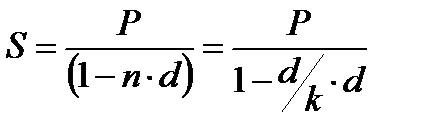
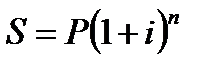
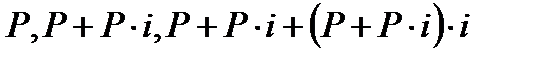 или
или 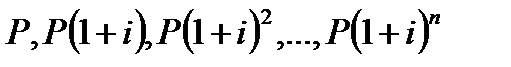
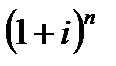 - сложный дискурсивный коэффициент
- сложный дискурсивный коэффициент