
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретическая характеристика насоса по напорам.Содержание книги
Поиск на нашем сайте
Эта часть теоретической характеристики состоит из трех графиков и соответственно строится в три этапа. а) Вначале строится график Аналитической основой для построения этого графика является формула (25). Из этой формулы видно, что величина б) Затем строится график НТ = f(Q). Этот график отличается от графика в) Наконец, строится график Аналитической основой для построения этого графика служит формула (24), в которой величина
где А - коэффициент пропорциональности, не зависящий от режима работы насоса, т.е. А не зависит от Q.
Независимость А от Q позволяет определить значение А при расчетных значениях Q = Qр и А = При этом величина АНРГ определяется по формуле:
= где Отложив величину Аналитической основой для построения такой характеристики является формула (27). Используется уже построенная характеристика насоса по напорам В результате получается ряд значений Nr (при разных значениях Q), в том числе ранее рассчитанное значение Nr в расчетном режиме работы насоса ( График зависимости Nr от Q имеет вид квадратичной параболы, поскольку величина Nr через величину
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.180.149 (0.006 с.) |

 = f(Q)
= f(Q) снижается пропорционально увеличению Q, причем график зависимости
снижается пропорционально увеличению Q, причем график зависимости  , а вторая соответствует значениям Q = 0 и
, а вторая соответствует значениям Q = 0 и  . Величина U2 =UP2 = соnst известна из предыдущих расчетов, причем постоянной эта величина является по той причине, что nр=n=соnst (формула 22).
. Величина U2 =UP2 = соnst известна из предыдущих расчетов, причем постоянной эта величина является по той причине, что nр=n=соnst (формула 22). тем, что в нем учитывается влияние конечного числа лопаток рабочего колеса. Значения Нт на графике Нт = f(Q) получаются умножением значений
тем, что в нем учитывается влияние конечного числа лопаток рабочего колеса. Значения Нт на графике Нт = f(Q) получаются умножением значений  . После нанесения этой одной точки график НТ = f(Q) проводится параллельно графику
. После нанесения этой одной точки график НТ = f(Q) проводится параллельно графику 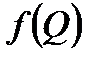 .
. .
. зависит от Q. Построение графика
зависит от Q. Построение графика  в масштабе для напоров значений гидравлических потерь напора в насосе
в масштабе для напоров значений гидравлических потерь напора в насосе  Нr. Величины
Нr. Величины  , (31)
, (31)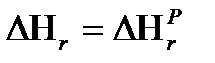 по формуле:
по формуле: (32)
(32)
 (33)
(33) и
и  - принимаются из предыдущих расчетов, а величина
- принимаются из предыдущих расчетов, а величина  .
. от точки графика
от точки графика  и Qр, можно получать первую точку графика
и Qр, можно получать первую точку графика  (формула 31) и эти значения наносятся в масштабе для напоров вниз от графика
(формула 31) и эти значения наносятся в масштабе для напоров вниз от графика  подставляются принимаемые значения Q и
подставляются принимаемые значения Q и  .
. ).
).


