
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение сил, действующих на поршень и поршневой палецСодержание книги
Поиск на нашем сайте
Сила давления газов определяется по формуле:
где
Справа от свернутой диаграммы изображаем оси развернутой диаграммы. При этом ось абсцисс развернутой диаграммы смещаем вверх по вертикали относительно оси абсцисс свернутой диаграммы на величину атмосферного давления Р0. Отрезок Vh, представляющий рабочий объем цилиндра и в то же время в соответствующем масштабе ход поршня, делим пополам и радиусом, равным половине Vh, описываем полуокружность из точки Ц. Вправо от точки Ц откладываем отрезок ЦБ (л), равный
Точки пересечений сносим (проецируем) на перпендикуляры, восстановленные к оси абсцисс развернутой диаграммы из точек, соответствующих углам поворота кривошипа коленчатого вала. Кривая, проведенная через полученные точки, является развернутой индикаторной диаграммой за рабочий цикл. Например, при
Сила инерции возвратно-поступательно движущихся масс кривошипно-шатунного механизма:
где
С учётом правила знаков
Входящая в уравнение масса Значит Так как
Угловая частота вращения коленчатого вала берётся при номинальном скоростном режиме двигателя, т. е.
Радиус кривошипа
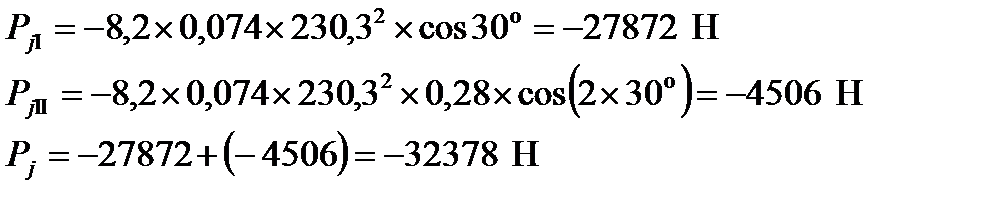
Результаты расчета удельных сил инерции заносим в таблицу 4.1: Таблица 4.1
Суммарная удельная сила, действующая на поршень, определяется как алгебраическая сумма сил, соответствующих углам поворота коленчатого вала: Pрез = Pг+ Pj. Например, при
Силы инерции от вращательно движущихся масс (Н) Рs = -mшк·R·ω2·10-6, где mшк = 0,725mш = 0,725·8 = 5,8. Рs = -5,8·0,074·(230,3)2·10-6 = -0,0023 Н. Результаты расчёта сил Таблица 4.1 Результаты динамического расчёта
 и и 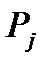 определить необходимо и графически. Для этого из общего центра О проводим две полуокружности. Одна радиусом определить необходимо и графически. Для этого из общего центра О проводим две полуокружности. Одна радиусом 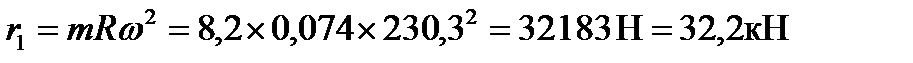 , в масштабе , в масштабе  и другую радиусом и другую радиусом  . Проводим ряд лучей под углами . Проводим ряд лучей под углами 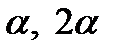 и т. д. к вертикали. Вертикальные проекции отрезков лучей, пересекающих первую окружность, дают в принятом масштабе значении сил и т. д. к вертикали. Вертикальные проекции отрезков лучей, пересекающих первую окружность, дают в принятом масштабе значении сил 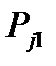 , а проекции тех же лучей, пересекающих вторую окружность при соответствующих углах поворота коленчатого вала, дают значения сил , а проекции тех же лучей, пересекающих вторую окружность при соответствующих углах поворота коленчатого вала, дают значения сил 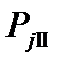 , при углах поворота соответственно вдвое меньших. , при углах поворота соответственно вдвое меньших.Проводим через центр О горизонтальную прямую и откладываем на ней значения По точкам пересечения указанных проекций с ординатами, проходящими через соответствующие значения углов
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.60.175 (0.008 с.) |

 (4.1)
(4.1)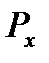 - текущее значение давление газов по индикаторной диаграмме,
- текущее значение давление газов по индикаторной диаграмме, 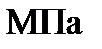 .
.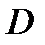 - диаметр цилиндра,
- диаметр цилиндра,  .
.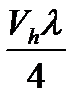 =
= 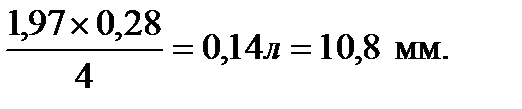
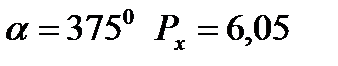 МПа
МПа
 , (4.2)
, (4.2)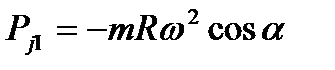 - сила инерции первого порядка, период изменения которой равен одному обороту коленчатого вала
- сила инерции первого порядка, период изменения которой равен одному обороту коленчатого вала  ;
;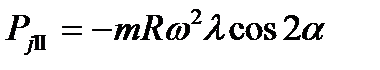 - сила инерции второго порядка, период изменения которой равен половине оборота коленчатого вала, т. е.
- сила инерции второго порядка, период изменения которой равен половине оборота коленчатого вала, т. е. 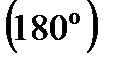 .
.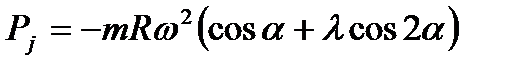 (4.3)
(4.3) движущихся возвратно-поступательно деталей КШМ, может быть при ориентировочных расчётах представлена суммой
движущихся возвратно-поступательно деталей КШМ, может быть при ориентировочных расчётах представлена суммой 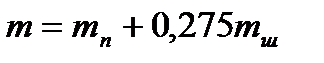 , где
, где 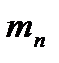 - масса поршневого комплекта
- масса поршневого комплекта  , а
, а 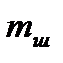 - масса шатуна
- масса шатуна  .
. и
и 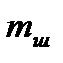 принимаем, ориентируясь табличными данными [4, стр.57] в зависимости от диаметра цилиндра
принимаем, ориентируясь табличными данными [4, стр.57] в зависимости от диаметра цилиндра 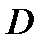 .
.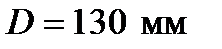 и согласно таблице
и согласно таблице  , то выбираем
, то выбираем 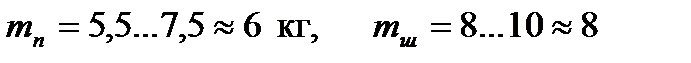 .
.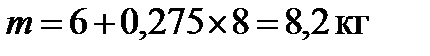
 (4.4)
(4.4) пример расчёта
пример расчёта 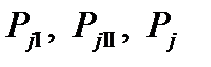 , при
, при 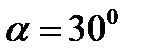 .
.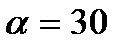 0:
0:
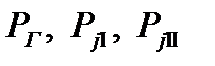 и
и  сводим в таблицу 4.1.
сводим в таблицу 4.1.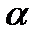 ,
град
,
град
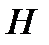

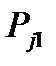
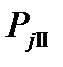
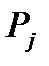

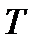

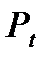



 углов поворота коленчатого вала за рабочий цикл
углов поворота коленчатого вала за рабочий цикл  .
.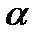 на оси абсцисс, строим кривые
на оси абсцисс, строим кривые 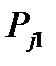 и
и 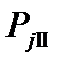 а затем суммируем ординаты кривых, получаем кривую результирующей силы инерции
а затем суммируем ординаты кривых, получаем кривую результирующей силы инерции  .
.


