
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЭДС катушечных групп и фазы.Содержание книги Поиск на нашем сайте
Катушечная группа состоит из q одинаковых катушек (секций), расположенных в соседних пазах (рисунок 12). Рисунок 12 – Катушечная группа ЭДС в катушках сдвинуты по фазе на угол αэл. Все секции катушечной группы сдвинуты последовательно. Суммарная ЭДС равна геометрической сумме отдельных (рисунок 13). Рисунок 13 – Секции катушечной группы Эта сумма меньше арифметической суммы Еq1<qEk1. Отношение
Суммарная ЭДС катушечной группы равна
Двухслойная обмотка фазы состоит из 2р катушечных групп, а однослойная – из р групп. Катушечные группы могут быть соединены последовательно, параллельно или последовательно-параллельно. Все катушечные группы состоят из q катушек с числом витков wk. Если обмотка фазы состоит из а параллельных ветвей, то общее число последовательно соединенных витков фазы, определяющее ее ЭДС равно: – для двухслойной обмотки
– для однослойной обмотки
Тогда ЭДС фазы обмотки от поля первой гармоники равно
Улучшение формы кривой ЭДС. В обмотке фазы кроме ЭДС первой гармоники индуцируется ЭДС от высших гармоник магнитного поля. ЭДС то высших гармоник определяется по формуле
где fν=ν∙f1 – частота ν-ой гармоники; Фν – магнитный поток ν-ой гармоники; Кνy, Крν – соответственно коэффициенты укорочения и распределения для ν-ой гармоники. Число полюсов для ν-ой гармоники в ν раз больше, чем для первой. Поэтому электрические углы сдвига фаз между ЭДС для высших гармоник будут в ν раз больше, чем для первой. С учетом этого имеем
Результирующая ЭДС (действующее значение) фазы равно
Укорочение шага обмотки и распределение ее по пазам приводит к уменьшению ЭДС высших гармоник. При укорочении шага обмотки происходит более резкое уменьшение ЭДС высших гармоник. При укорочении шага на 1/ν часть полюсного деления в кривой ЭДС полностью исчезает ν-ая гармоника. При у=τn ЭДС пятой гармоники в проводниках обмотки под противоположными полюсами суммируются (рисунок 14). При у=
Рисунок 14 – ЭДС пятой гармоники При выборе шага обмотки стремятся, чтобы были полностью исключены и значительно ослаблены ЭДС наиболее сильно проявляемых гармоник. Это третья, пятая и седьмая гармоники. Третью гармонику в линейной ЭДС обычно уничтожают соединением трехфазной обмотки в звезду. Для ослабления пятой и седьмой гармоник шаг обмотки выбирают в пределах от При увеличении числа пазов на q на полс и фазу сильно уменьшается коэффициенты распределения Кρν. Это объясняется тем, что ЭДС катушек катушечных групп для ν-ых гармоник будут сдвинуты относительно друг друга на угол, в ν раз больший, чем для первой гармоники, вследствие чего их геометрическая сумма уменьшается. Кривая результирующей ЭДС обмотки с большим q ближе к синусоиде. Однако при этом машина становится дороже. Обычно q=2…6. Пульсации магнитного поля возникают вследствие зубчатого строения статора и ротора. Эти гармоники называются зубчатыми. Их порядок зависит от числа зубцов (рисунок 15).
Рисунок 15 – Зубчатое строение статора
Для уменьшения зубцовых гармоник в кривой ЭДС изменяют скос пазов или скос полюсов. Если скос выполняется на статоре, то он производится на одно зубцовое деление ротора, а если на роторе, то на одно зубцовое деление статора. При скосе пазов можно полностью уничтожить зубцовые гармоники. Физически это можно объяснить тем, что у зубцевых гармоник магнитное поле под зубцом и пазом имеет противоположную полярность. Вследствие этого в отдельных участках проводника, расположенного в скошенном пазу противоположного магнитного провода, индуцируются одинаковые по величине, но противоположно направленные ЭДС. Их сумма равна нулю (рисунок 16). Рисунок 16 – Скос пазов
При скосе пазов уменьшается ЭДС первой гармоники. Это учитывается коэффициентом скоса Кск. Для определения Кск заменим проводник в скошенном пазу некоторым числом прямых проводников очень малой длины. Геометрическая сумма ЭДС этих малых проводников будет равна хорде окружности радиуса R, на которую опираются стороны угла γс (рисунок 17)
Коэффициент скоса Кск равен отношению геометрической сумме ЭДС к арифметической
Для ν-ой гармоники
В общем случае ЭДС фазы определяется по формулам: для общей гармоники
для ν-ой гармоники
где МДС катушек. Ток в обмотке создает магнитодвижущую силу (МДС). Предположим, что на статоре двухполюсной машины размещена катушка с числом витков wk и шагом у=τn. Ротор представляет собой цилиндр. Зазор между статором и ротором равномерный. Если в катушке синусоидальный ток Рисунок 18 – Магнитное поле катушки МДС действует по замкнутому контуру, образованному магнитными силовыми линиями, и равна полному току, охваченному этим контуром. Все линии сцеплены с катушкой и полный ток для них равен ik∙wk. МДС по всей ширине катушки имеет одно и то же значение. Обе части машины относительно оси х-х симметричны, поэтому на каждую половину магнитной цепи приходится половина МДС катушки. Ее можно считать за МДС, приходящуюся на один полюс. Распределение МДС на полюсных делениях показано на рисунке 19. Рисунок 19 – Распределение МДС на полюсных делениях Здесь катушки имеют прямоугольную форму. Для различных моментов МДС остается неподвижной в пространстве, но изменяет свое значение и направление
где Таким образом, при протекании по катушке переменного тока создается пульсирующая МДС. Обычно прямоугольную МДС заменяют суммой гармоник, причем только нечетных, т.к. кривая МДС симметрична относительно оси абсцисс. МДС каждой гармоники также имеет пульсирующий характер. Для первой (основной) гармоники амплитуда будет равна
где Fk1 – амплитуда основной гармоники МДС катушки, образуемой током с амплитудой Если ось катушки (х=0) принять за начало отсчета, то МДС первой гармоники в любой точке полюсного деления, расположенной на расстоянии х от оси катушки, будет равна
Это уравнение волны, пульсирующей по времени по синусоидальному закону и распределенной в пространстве также по синусоидальному закону. Высшие гармоники МДС являются пространственными и имеют в ν раз больше число полюсов, чем первая гармоника. Поэтому полюсное деление ν-ой гармоники равно
где Высшие гармоники МДС стараются ослаби МДС фазы. Рассмотрим двухполюсную машину с однослойной обмоткой фазы, состоящей из q катушек с шагом у=τn и смещенных на одно зубцовое деление. Результирующая МДС катушечной группы (фазы) равна сумме прямоугольных МДС всех катушек. Результирующая МДС представляет собой ступенчатую фигуру, которая с увеличением q по форме приближается к синусоиде (рисунок 20). Если МДС катушек разложить в гармонический ряд, то результирующая МДС первой гармоники фазы будет равна сумме первых гармоник МДС катушек
где Кр1 – коэффициент распределения, определяемой по аналогичной формуле
Рисунок 20 – МДС катушек фазы
Двухслойные обмотки выполняются с укороченным шагом. Двухслойную обмотку можно представить как бы состоящей из двух однослойных обмоток с шагом у=τn, оси которых сдвинуты на электрический угол, равный (1-β)∙π рад (β=у/τ). Одна из этих обмоток располагается в верхнем слое, а другая – в нижнем. Каждая из однослойных обмоток создает МДС основной гармоники
Максимальное значение МДС первой гармоники фазы для двухслойной обмотки будет равно
где Рисунок 21 – Максимальное зачение МДС первой гармоники фазы МДС первой гармоники можно определить по формуле
где Если имеется скос пазов, то вводится коэффициент скоса Первая гармоника МДС фазы неподвижна в пространстве, имеет синусоидальное пространственное распределение и пульсирует во времени с частотой протекающего по обмотке тока
В фиксированной точке х полюсного деления для любого момента времени первая гармоника будет равна
Коэффициента х отсчитывается от оси катушечной группы. Для высших гармоник МДС имеем
где
Для уменьшения МДС ν-ых гармоник и ее приближения к синусоиде обмотку фазы выполняют с укороченным шагом и распределяют ее по пазам
|
|||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.190 (0.011 с.) |

 – коэффициент распределения обмотки. Его величину можно определить с помощью векторной диаграммы. Рассматривая векторы ЕК как часть многоугольника, вписанного в окружность радиуса R, получим
– коэффициент распределения обмотки. Его величину можно определить с помощью векторной диаграммы. Рассматривая векторы ЕК как часть многоугольника, вписанного в окружность радиуса R, получим .
.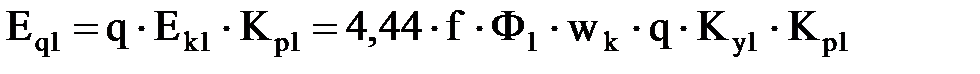 .
. ;
; .
. .
. , (13)
, (13)
 .
. ЭДС пятой гармоники в проводниках обмотки вычитаются. Поэтому пятая гармоника будет отсутствовать. При этом также уменьшаются ЭДС других гармоник.
ЭДС пятой гармоники в проводниках обмотки вычитаются. Поэтому пятая гармоника будет отсутствовать. При этом также уменьшаются ЭДС других гармоник. до
до  . При
. При  При
При 
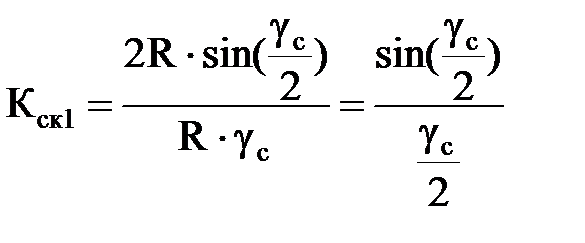 .
. .
. (14)
(14) (15)
(15) – обмоточные коэффициенты.
– обмоточные коэффициенты. , то он создает магнитное поле, как показано на рисунке 18.
, то он создает магнитное поле, как показано на рисунке 18. ,
, – максимальное значение МСД катушки на одном полюсе.
– максимальное значение МСД катушки на одном полюсе. ,
,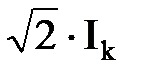 , определяемая соотношением
, определяемая соотношением  .
.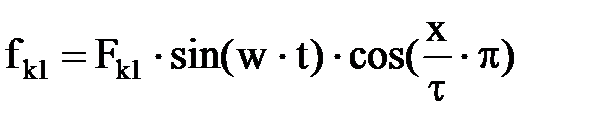 .
. . С учетом этого МДС в ν-ой гармонике равна
. С учетом этого МДС в ν-ой гармонике равна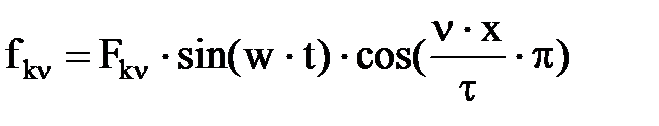 ,
, – амплитуда ν-ой гармоники МДС.
– амплитуда ν-ой гармоники МДС. ,
, .
. .
. ,
, – коэффициент укорочения для первой гармоники. См. рисунок 21.
– коэффициент укорочения для первой гармоники. См. рисунок 21. ,
, для двухслойной обмотки с укороченным шагом и
для двухслойной обмотки с укороченным шагом и  для однослойной обмотки.
для однослойной обмотки. .
. .
. .
.
 – максимальное значение МДС фазы для ν-ой гармоники;
– максимальное значение МДС фазы для ν-ой гармоники; – обмоточный коэффициент для ν-ой гармоники.
– обмоточный коэффициент для ν-ой гармоники. ;
; .
.


