
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обмотки с дробным числом пазов. Эдс катушек.Содержание книги
Поиск на нашем сайте
Обмотки с дробным числом пазов на полюс и фазу применяются в многополюсных машинах, в которых из-за ограниченности полюсного деления q может быть небольшим. Улучшается форма кривой ЭДС. Чтобы двухслойная обмотка с дробным числом пазов на полюс и фазу была симметричной, т.е. в обмотке ЭДС фаз были равны и сдвинуты по фазе на угол 1200, необходимо выполнить условие Z/(3t) – целое число, где t – общий наибольший делитель общего числа пазов машины Z и числа пар полюсов pn. Распределение пазов, а следовательно, катушек и катушечных групп по фазам производится следующим образом. Дробное q=b+c/d представляется в виде неправильной дроби q=N/d (b – целая часть дробного q; с<d – числитель и знаменатель его дробной части, N=b∙d+c – числитель неправильной дроби). Составляют таблицу с числом строк, равным числу полюсов 2pn и числом клеток в строке, равным 3N. Таблицу делят на три одинаковых по ширине столбца (в каждом N клеток по горизонтали). Затем в клетке с шагом равным d, в последовательном порядке вписывают номера пазов с первого до Z. Номера пазов в столбцах показывают, что в них располагаются верхние стороны катушек одной фазы. Затем с шагом у производят соединение верхних сторон катушек с нижними. Рассмотрим пример. Построим петлевую трехфазную обмотку с данными: Z=27; 2pn=6; y=4. Число q равняется
Составляем таблицу с числом строк, равным 2pn=6, числом клеток в строке равным 3N=9 и впишем в нее номера пазов. По таблице построим схему обмотки одной фазы А при шаге у=4 (рисунок 6).
Катушечные группы состоят из различного числа катушек и чередуются с определенной периодичностью. Дробному q соответствует среднее число катушек в катушечной группе. В электромагнитном отношении эта обмотка обмотке с целым q при q=N. При вращении магнитного поля относительно проводников обмотки в ней индуцируется ЭДС. Она переменная, т.к. относительно проводников поочередно проходят полюсы разной полярности. Частота переменной ЭДС
Обычно требуется, чтобы ЭДС была практически синусоидальной. Форма кривой ЭДС зависит от формы кривой распределения магнитного поля на полюсном делении. Получить синусоидальное распределение этого поля практически невозможно. Улучшение кривой ЭДС достигается за счет правильного выбора схемы обмотки, для чего она выполняется распределенной с укороченным шагом. ЭДС в обмотке фазы есть сумма ЭДС всех катушек. Катушка состоит из Wk витков, которые размещаются в одних и тех же пазах, поэтому можно считать, что все витки в магнитном поле будут находиться в одинаковых условиях. Виток образуется последовательным соединением двух проводников, расположенных в разных пазах на расстоянии у друг от друга. Мгновенное значение индуцированной ЭДС
При Рисунок 7 – Кривая индукции проводника Кривую распределения индукции Гармоники кривой магнитного поля называются изопространственными, т.к. распределение является функцией пространственных координат и от времени не зависит. У каждой гармоники увеличивается количество полюсов и уменьшается полюсное деление пропорционально порядку гармоники (рисунок 8).
Рисунок 8 – Разложение кривой индукции проводника Магнитное поле каждой гармоники индуцирует ЭДС в обмотке. От поля первой гармоники
где Еmn1=Bδm1∙
При расчете ЭДС удобно исходить из потока на полюсном делении. Для первой гармоники
где Вср1 – среднее значение индукции; τ – полюсное деление, определяемое как τ= Т.к. для синусоиды
выразим из формулы 7
используя формулы 6, 7, 8 и подставляя полученные значения в формулу 5, имеем
учитывая, что
подставляем в формулу
При форме поля, отличной от синусоидальной, ЭДС в проводнике определяется по формуле
где КВ –коэффициент формы поля, равный При синусоидальном поле Для анализа обмоток и оценки некоторых их свойств удобно использовать векторные диаграммы, где первую гармонику ЭДС проводника изображают в виде временного вектора. Период изменения ЭДС в проводнике будет соответствовать перемещению магнитного поля относительно этого проводника на два полюсных деления, т.е. на 2π рад. За один оборот якоря ЭДС в проводнике изменится на р периодов или на 2π∙р рад (3600∙р). Проводники, расположенные в соседних пазах, имеют пространственный сдвиг
Витки катушки образованы из проводников, которые расположены в пазах, отстоящих друг от друга на расстоянии у=τn (рисунок 9). Рисунок 9 – Витки катушки
Следующие ЭДС в них сдвинуты по фазе на угол Проводники в витке включены встречно,?????? ЭДС витка равна геометрической разности ЭДС проводников. При у=τn геометрическая разность ЭДС проводников равна их геометрической сумме, т.е. Рисунок 10 – геометрическая сумма ЭДС проводников При укороченном шаге (у<τn) векторы ЭДС проводников сдвинуты на угол
где Ку1 – коэффициент укорочения шага катушки, определяемый как
Рисунок 11 – Векторная диаграмма
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.120.12 (0.011 с.) |




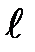 =const и v= const ЭДС пропорциональна нормальной составляющей индукции
=const и v= const ЭДС пропорциональна нормальной составляющей индукции  в том месте окружности якоря, где в данный момент находится рассматриваемый проводник. Кривая изменения ЭДС проводника во времени будет повторять форму кривой распределения индукции
в том месте окружности якоря, где в данный момент находится рассматриваемый проводник. Кривая изменения ЭДС проводника во времени будет повторять форму кривой распределения индукции 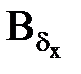 на протяжении двух полюсных делений машины (рисунок 7).
на протяжении двух полюсных делений машины (рисунок 7). ,
, (5)
(5) , (6)
, (6)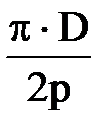 , где D – диаметр якоря.
, где D – диаметр якоря. , (7)
, (7)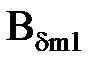
 , (8)
, (8) (9)
(9)
 . (10)
. (10) , (11)
, (11) .
.
 и их ЭДС не совпадают по фазе. Электрический угол сдвига фаз векторов ЭДС проводников в соседних пазах равен
и их ЭДС не совпадают по фазе. Электрический угол сдвига фаз векторов ЭДС проводников в соседних пазах равен .
. .
. (рисунок 10).
(рисунок 10).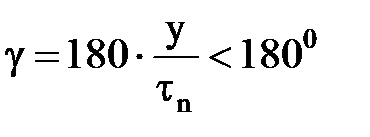 , поэтому их геометрическая разность меньше арифметической суммы (Еb1<2En1). В этом случае ЭДС витка можно определить из векторной диаграммы (рисунок 11)
, поэтому их геометрическая разность меньше арифметической суммы (Еb1<2En1). В этом случае ЭДС витка можно определить из векторной диаграммы (рисунок 11) , (12)
, (12) . ЭДС катушки, содержащей wk витков
. ЭДС катушки, содержащей wk витков



