Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи к контрольной работе № 1Содержание книги
Поиск на нашем сайте
1. Радиус-вектор материальной точки изменяется со временем по закону 2. Одно из тел бросили с высоты h1 =18 м вертикально вверх, другое в тот же момент с высоты h2 = 32 м бросили горизонтально. Определите начальную скорость 3. Воздушный шар поднимается с Земли вертикально вверх с ускорением 4. Тело брошено под углом а. к горизонту. Пренебрегая сопротивлением воздуха, определите этот угол, если максимальная высота подъема hmax меньше дальности полета s в п = 2,4 раза. 5. С вершины наклонной плоскости, составляющей с горизонтом угол 6. Радиус-вектор материальной точки, движущейся в поле тяготения Земли, описывается уравнением 7. Материальная точка начинает вращаться с постоянным угловым ускорением. Определите угловое ускорение 8. Диск радиусом R = 5 см вращается вокруг неподвижной оси так, что зависимость угловой скорости от времени задается уравнением 9. Скорость автомобиля (радиус колес R = 35 см), движущегося равнозамедленно, за время 10. Вентилятор после выключения за время t = 5,5 с, двигаясь равнозамедленно, сделал до остановки N= 22 оборота. Определите угловую скорость 11. Движение материальной точки массой т = 0,25 кг описывается уравнением 12. Шарик массой m = 200 г, подвешенный на нити длиной l = 56 см, совершает колебания в вертикальной плоскости. Сила натяжения нити Т, когда нить составляет угол 13. Через блок, укрепленный на конце стола, перекинута нерастяжимая нить, к концам которой прикреплены грузы, один из которых (т 1 = 400 г) движется по поверхности стола, а другой (т 2 = 600 г) — вдоль вертикали вниз. Коэффициент трения f груза о стол равен 0,1. Считая нить и блок невесомыми, определите: 1) ускорение а, с которым движутся грузы; 2) силу натяжения T нити. 14. Через невесомый блок перекинута невесомая нерастяжимая нить с грузами одинаковой массы 15. Определите ускорения а1 и а2 тел и натяжение нитей Т и Т1 в системе, представленной на рисунке. Масса одного тела т1 = 0,6 кг, масса другого т 2 = 0,4 кг. Нити невесомы и нерастяжимы, массой блока и силами трения пренебречь.
16. На наклонной плоскости с углом наклона 17. Брусок массой 18. Снаряд, вылетевший из орудия под некоторым углом к горизонту со скоростью 19. Две лодки (масса каждой вместе с рыбаком равна
м.
21. С башни высотой 22. Медную игральную кость с ребром 23. Конькобежец, разогнавшись до скорости 24. Мощность 25. Груз массой 26. Пренебрегая сопротивлением воздуха, определите отношение кинетической Т ипотенциальной энергии П шарика, брошенного под углом 27. Энергозатраты на откачку воды из подвала глубиной 28. Шарик массой т1 = 16 г, движущийся горизонтально, столкнулся с шаром массой т2 = 0,8 кг, висящим на прямом недеформируемом и невесомом стержне длиной l = 1,7 м. Считая удар упругим, определите скорость шарика 29. Шар, движущийся со скоростью 30. Два свинцовых шара массами
31. К стержню длиной
32. Сравните кинетические энергии двух шаров с одинаковыми плотностями, катящихся по плоскости с одинаковой скоростью, если радиус второго шара в 33. Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой массы и одинакового радиуса, катятся без скольжения с одинаковой скоростью. Определите, во сколько раз отличаются их кинетические энергии. 34. С наклонной плоскости, составляющей угол 35. Колесо массой т= 2,8 кг раскручивается постоянной касательной силой F = 15 Н. Пренебрегая трением, определите момент времени t, когда кинетическая энергия вращающегося колеса Твр = 3 кДж. 36. На однородный сплошной цилиндрический вал радиусом 37. Кинетическая энергия вращающегося с частотой 38. Через неподвижный блок, укрепленный на краю стола, перекинута нить, к которой привязаны три груза массами 39. На пружинных весах лежит гиря массой т = 1,2 кг, которая сжимает пружину на х1= 3 см. Определите, на какую величину 40. Человексидит в центре скамьи Жуковского, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой 41. Принимая, что масса Земли неизвестна, определите высоту h, на которой ускорение свободного падения 42. Определите среднюю плотность 43. Радиус некоторой планеты R' в п = 3 раза больше радиуса Земли Ro. Определите продолжительность суток Т' на планете, если тела на ее экваторе невесомы. Ускорение свободного падения 44. Радиус некоторой планеты R = 3800 км, продолжительность суток Т = 40 ч. Определите массу М этой планеты, если на полюсе тела весят в п = 1,2 раза больше, чем на экваторе. 45. Искусственный спутник вращается вокруг Земли по окружности на высоте h=2 Мм. Считая массу Земли неизвестной, определите период Т обращения спутника, если радиус Земли Ro = 6,37 • 106 м. 46. Определите работу сил поля тяготения при перемещении тела массой т = 12 кг из точки 1, находящейся от центра Земли на расстоянии 47. Определите высоту h, на которую можно поднять с Луны ракету массой т = 2 т, если при этом совершается работа А = 1 ГДж. Какую энергию Т надо затратить, чтобы запустить ракету по круговой орбите с данной высоты? Масса Луны М= 7,33 • 1022 кг, радиус Луны R = 1,74 • 106 м. 48. Определите числовое значение первой космической скорости для Луны, если ускорение свободного падения у поверхности Луны 49. При вертикальной посадке на Луну ракета последние 120 м пути, двигаясь равнозамедленно, прошла за время t = 6,5 с. Определите вес Р космонавта перед посадкой, если его масса m = 70 кг. Радиус Луны R = 1740 км масса Луны М= 7,35 • 1022 кг. 50. Вертикальный стержень укреплен на горизонтальном диске, вращающемся с частотой п = 0,8 с-1. К вершине стержня привязан шарик на нити длиной l = 0,12 м. Определите расстояние от стержня до оси вращения если угол 51. Полый шар плавает на границе двух несмешивающихся жидкостей так, что соотношение частей шара во второй и первой жидкости равно 52. В стакан с водой, уравновешенный на рычажных весах, опустили подвешенный на нити латунный шарик массой 53. В сообщающиеся трубки с водой площадью сечения 54. Два мальчика массами 55. Определите силу 56. Открытый цилиндрический сосуд, стоящий на ножках высотой
57. Цилиндрический сосуд высотой 58. Водомер представляет собой горизонтальную трубу переменного сечения, в которую впаяны две вертикальные манометрические трубки одинакового сечения. По трубе протекает вода. Пренебрегая вязкостью воды, определите ее массовый расход, если разность уровней в манометрических трубках
59. Пренебрегая вязкостью воды, определите объем 60. Пробковый шарик радиусом 61. Определите число N молекул воды в бутылке вместимостью 0,33 л. Молярная масса воды 62. В баллоне вместимостью 63. Газ в баллоне под давлением 64. В закрытом сосуде при температуре 300 К и давлении 0,1 МПа находятся 10 г водорода и 16 г гелия. Считая газы идеальными, определите удельный объем 65. Кислород массой 66. B баллоне вместимостью 67. В сосуде вместимостью 68. Определите среднюю арифметическую скорость 69. Исходя из основного уравнения молекулярно-кинетической теории идеальных газов, выведите связь между давлением 70. Определите среднюю кинетическую энергию 71. Определите среднюю кинетическую энергию 72. Азот массой т= 5 г находится под давлением 100 кПа при температуре 17° С. После нагревания при постоянном давлении газ занял объем 10 л. Определите: 1) количество теплоты Q, полученное газом; 2) изменение внутренней энергии 73. Определите удельные теплоемкости 74. При изохорном нагревании азота объемом 10 л давление газа изменилось на 75. Азот (N2) массой 14 г находится при температуре 27 °С. В результате изобарного расширения (см. рисунок) объем газа увеличился в 2 раза. Определите: 1) изменение внутренней энергии 76. При изобарном расширении двухатомного газа была совершена работа А=1 кДж. Определите количество теплоты Q, переданное газу. 77. Азот массой т= 100 г (молярная масса 78. Газ массой m = 10 г расширяется изотермически от объема 79. Некоторый газ массой m = 1 г и первоначальным удельным объемом, находящийся при температуре Т = 280 К и под давлением р1 = = 0,1 МПа, сжимают изотермически до давления р2 = 1 МПа. Определите: 1) какой это газ; 2) работу А, затраченную на сжатие газа. 80. Многоатомный идеальный газ из одного и того же состояния расширяется один раз при постоянной температуре, другой — при постоянном давлении. В обоих случаях работа расширения газа одинакова. Начертите графики этих процессов. В котором из рассматриваемых процессов и во сколько раз количество подведенной к газу теплоты больше? 81. Азот массой m = 56 г, находящийся при нормальных условиях, расширяется адиабатно, причем объем газа увеличивается в два раза. Определите: 1) изменение внутренней 82. Определите число i степеней свободы газа, если он расширяется адиабатно и при этом его объем увеличивается в четыре раза, а термодинамическая температура уменьшается в 1,74 раза. 83. Двухатомный идеальный газ совершает процесс, в ходе которого молярная теплоемкость С газа остается постоянной и равной 84. Некоторый двухатомный газ подвергают политропному сжатию, в результате чего давление газа возросло от р1 = 10 кПа до р2 = 30 кПа, а объем газа уменьшился от V1 = 2,5 л до V2 = 1 л. Определите: 1) показатель политропы п; 2) изменение внутренней энергии 85. В сосуде, теплоемкость которого 0,6 кДж/К, находится 0,5 л воды и 300 г льда при 0 °С. Определите, какая установится температура после впуска в воду 100 г водяного пара при температуре 100 °С. Удельная теплота парообразования 2,26 МДж/кг, удельная теплота плавления льда 3,35 • 105 Дж/кг, плотность вод 1 г/см3, удельная теплоемкость воды 4,19 • 103 Дж/(кг • К). 86. В идеальной тепловой машине Карно, работающей по обратному циклу (холодильной машине), в качестве холодильника используется вода при 0 °С, а в качестве нагревателя — вода при 100 °С. Сколько воды m 2 следует заморозить в холодильнике, чтобы превратить в пар 100 г воды в нагревателе? Удельная теплота плавления льда 87. Идеальный газ количеством вещества
88. Идеальный трехатомный газ количеством вещества v = 2 моль занимает объем V1 = 10 л и наход
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 926; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.149 (0.015 с.) |

 где А = 0,4 м/с2, В = 0,1 м/с;
где А = 0,4 м/с2, В = 0,1 м/с;  и
и 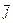 — орты координатных осей х и у. Определите выражения для
— орты координатных осей х и у. Определите выражения для  и
и  ; модули скорости и ускорения, тангенциальную и нормальную составляющие ускорения в момент времени t = 2 с.
; модули скорости и ускорения, тангенциальную и нормальную составляющие ускорения в момент времени t = 2 с. первого тела, если оба тела на Землю упали одновременно.
первого тела, если оба тела на Землю упали одновременно. 0.9 м/с2. Через
0.9 м/с2. Через  12 с после начала его движения пассажир уронил гайку. Определите время
12 с после начала его движения пассажир уронил гайку. Определите время 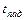 падения гайки на Землю; ее скорость
падения гайки на Землю; ее скорость  в момент удара о Землю.
в момент удара о Землю. 37
37  , горизонтально брошен камень со скоростью
, горизонтально брошен камень со скоростью  8 м/с. Пренебрегая сопротивлением воздуха, определите расстояние l до точки падения камня на наклонную плоскость и угол
8 м/с. Пренебрегая сопротивлением воздуха, определите расстояние l до точки падения камня на наклонную плоскость и угол  между вектором скорости
между вектором скорости  камня в момент его падения и наклонной плоскостью.
камня в момент его падения и наклонной плоскостью.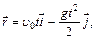 где
где  ускорение свободного падения;
ускорение свободного падения;  орты координатных осей х и у. Определите момент времени
орты координатных осей х и у. Определите момент времени  после начала движения, когда вектор скорости
после начала движения, когда вектор скорости  точки направлен под углом
точки направлен под углом  к горизонту. Чему равна скорость
к горизонту. Чему равна скорость  в этот момент времени?
в этот момент времени? точки, если через промежуток времени t = 5 с угол
точки, если через промежуток времени t = 5 с угол  между векторами полного ускорения
между векторами полного ускорения  и скорости
и скорости  (
( 2 рад/с2,
2 рад/с2, 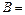 1 рад/с5). Определите для точек на ободе диска к концу первой секунды после начала движения: 1) полное ускорение; 2) число оборотов, сделанных диском.
1 рад/с5). Определите для точек на ободе диска к концу первой секунды после начала движения: 1) полное ускорение; 2) число оборотов, сделанных диском. = 2 с уменьшилась с
= 2 с уменьшилась с  = 65 км/ч до
= 65 км/ч до  = 46 км/ч. Определите угловое ускорение
= 46 км/ч. Определите угловое ускорение 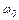 и частоту вращения п вентилятора в рабочем режиме, а также угловое ускорение вентилятора
и частоту вращения п вентилятора в рабочем режиме, а также угловое ускорение вентилятора  где А = 2 м;
где А = 2 м;  = 0,7 рад/с;
= 0,7 рад/с;  — орты координатных осей х и у. Определите путь s, пройденный точкой за время
— орты координатных осей х и у. Определите путь s, пройденный точкой за время  1,4 кг. На один из грузов положен перегрузок массой
1,4 кг. На один из грузов положен перегрузок массой  0,2 кг. Считая, что грузы первоначально находились на одном уровне и пренебрегая трением, определите разность высот
0,2 кг. Считая, что грузы первоначально находились на одном уровне и пренебрегая трением, определите разность высот  , на которых будут находиться грузы через промежуток времени t = 1 с.
, на которых будут находиться грузы через промежуток времени t = 1 с.
 . Определите коэффициент трения f между бруском и наклонной плоскостью, если брусок начинает скользить, когда сила
. Определите коэффициент трения f между бруском и наклонной плоскостью, если брусок начинает скользить, когда сила  7,5 Н.
7,5 Н. 0,4, между доской и горизонтальной поверхностью трение отсутствует. Определите, при какой минимальной силе
0,4, между доской и горизонтальной поверхностью трение отсутствует. Определите, при какой минимальной силе  , приложенной к доске, брусок начнет скользить по доске.
, приложенной к доске, брусок начнет скользить по доске. ,в верхней точке траектории разрывается на два осколка, причем масса первого
,в верхней точке траектории разрывается на два осколка, причем масса первого  в
в 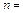 1,4 раза меньше массы второго
1,4 раза меньше массы второго  . Меньший из осколков полетел горизонтально в обратном направлении со скоростью
. Меньший из осколков полетел горизонтально в обратном направлении со скоростью  от орудия упадет больший осколок, если место разрыва отстоит от места выстрела на расстояние
от орудия упадет больший осколок, если место разрыва отстоит от места выстрела на расстояние  2,1 км (по горизонтали). Сопротивление воздуха не учитывать.
2,1 км (по горизонтали). Сопротивление воздуха не учитывать.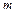 ) движутся со скоростями
) движутся со скоростями  2,2 м/с и
2,2 м/с и  1,9 м/с, причем скорость второй лодки направлена под углом
1,9 м/с, причем скорость второй лодки направлена под углом  и
и 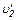 после обмена мешками.
после обмена мешками. 20. Определите положение центра масс (радиус-вектор центра масс
20. Определите положение центра масс (радиус-вектор центра масс 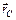 и его модуль
и его модуль  ) системы, состоящей из трех материальных точек массами
) системы, состоящей из трех материальных точек массами  1,4 кг,
1,4 кг,  1,2 кг и
1,2 кг и  1,8 кг, находящихся в вершинах равностороннего треугольника со стороной
1,8 кг, находящихся в вершинах равностороннего треугольника со стороной  15 м под углом
15 м под углом  12м/с брошено тело массой
12м/с брошено тело массой  8,93 г/см3.
8,93 г/см3. 21 км/ч, въезжает на горку с уклоном
21 км/ч, въезжает на горку с уклоном  1,6 м. Определите коэффициент трения
1,6 м. Определите коэффициент трения 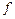 коньков о лед.
коньков о лед. двигателей самолета массой
двигателей самолета массой  самолета перед взлетом.
самолета перед взлетом. 20°, 2)
20°, 2) 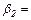 0° с горизонталью.
0° с горизонталью. 2 м, длиной
2 м, длиной 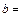 6 м составили
6 м составили  400 кДж. Определите коэффициент полезного действия
400 кДж. Определите коэффициент полезного действия  насоса, если уровень воды составлял
насоса, если уровень воды составлял  0,8 м от дна подвала. Плотность воды
0,8 м от дна подвала. Плотность воды  1 г/см3.
1 г/см3. 20°.
20°. налетает на покоящийся шар, масса которого в п = 1,5 раза больше первого. Определите отношение скорости
налетает на покоящийся шар, масса которого в п = 1,5 раза больше первого. Определите отношение скорости  70 см. Первоначально шары соприкасаются между собой, затем меньший шар отклонили на угол
70 см. Первоначально шары соприкасаются между собой, затем меньший шар отклонили на угол  , на которую поднимутся шары после удара; 2) энергию
, на которую поднимутся шары после удара; 2) энергию 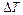 , израсходованную на деформацию шаров при ударе.
, израсходованную на деформацию шаров при ударе.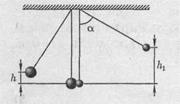
 1,2 кг и радиусом
1,2 кг и радиусом  0,25 м (см. рисунок). Определите момент инерции
0,25 м (см. рисунок). Определите момент инерции  системы относительно оси ОО', проходящей через незакрепленный конец стержня параллельно образующей цилиндра.
системы относительно оси ОО', проходящей через незакрепленный конец стержня параллельно образующей цилиндра.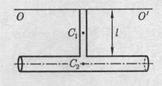
 3 раза меньше радиуса первого.
3 раза меньше радиуса первого. 20 см намотана невесомая нить, к концу которой подвешен груз массой 2 кг. Груз, разматывая нить, опускается с ускорением
20 см намотана невесомая нить, к концу которой подвешен груз массой 2 кг. Груз, разматывая нить, опускается с ускорением  3 с-1 маховика равна 8,4 кДж. Во сколько раз увеличится частота вращения маховика за время t = 5 с если на маховик начинает действовать ускоряющий момент силы М= 100 Н • м.
3 с-1 маховика равна 8,4 кДж. Во сколько раз увеличится частота вращения маховика за время t = 5 с если на маховик начинает действовать ускоряющий момент силы М= 100 Н • м. 800 г,
800 г,  пройдет от начала движения до того момента, когда кинетическая энергия вращения блока будет Твр = 1,1 Дж.
пройдет от начала движения до того момента, когда кинетическая энергия вращения блока будет Твр = 1,1 Дж. уменьшится длина пружины, если совершить дополнительную работу по ее сжатию А = 1,4 Дж.
уменьшится длина пружины, если совершить дополнительную работу по ее сжатию А = 1,4 Дж.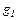 будет в п = 3 раза меньше, чем ускорение свободного падения у поверхности Земли
будет в п = 3 раза меньше, чем ускорение свободного падения у поверхности Земли  . Радиус Земли R0 = 6,37 • 106 м.
. Радиус Земли R0 = 6,37 • 106 м. грунта Луны, если известно, что ускорение свободного падения у поверхности Луны
грунта Луны, если известно, что ускорение свободного падения у поверхности Луны  1,7 м/с2, а ее радиус R = 1,74Мм.
1,7 м/с2, а ее радиус R = 1,74Мм. у поверхности планеты в
у поверхности планеты в  1,2 раза больше ускорения свободного падения у поверхности Земли. Период суточного вращения Земли Т = 24 ч.
1,2 раза больше ускорения свободного падения у поверхности Земли. Период суточного вращения Земли Т = 24 ч. в точку 2, находящуюся от ее центра на расстоянии
в точку 2, находящуюся от ее центра на расстоянии  , где
, где  радиус Земли.
радиус Земли. нити с вертикалью равен 37°.
нити с вертикалью равен 37°. . Плотности жидкостей и тела соответственно равны
. Плотности жидкостей и тела соответственно равны 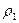 = 0,8 г/см3,
= 0,8 г/см3,  = 1 г/см3 и
= 1 г/см3 и  = 2,7 г/см3. Определите объем шара
= 2,7 г/см3. Определите объем шара  , если размер его внутренней полости
, если размер его внутренней полости  = 20 см3.
= 20 см3.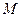 = 400 г так, чтобы он не касался дна. Определите массу
= 400 г так, чтобы он не касался дна. Определите массу 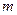 гирьки, с помощью которой можно уравновесить весы. Плотность материала шарика
гирьки, с помощью которой можно уравновесить весы. Плотность материала шарика  = 0,5 см2 долили в левую масло объемом
= 0,5 см2 долили в левую масло объемом  = 40 мл, в правую керосин объемом
= 40 мл, в правую керосин объемом  = 30 мл. Определите разность
= 30 мл. Определите разность  установившихся уровней воды в трубках, если плотность воды
установившихся уровней воды в трубках, если плотность воды  = 20кг и
= 20кг и  = 25 кг катаются на льдинах. Определите минимальную площадь
= 25 кг катаются на льдинах. Определите минимальную площадь  льдины, способной удержать их обоих, если толщина льда
льдины, способной удержать их обоих, если толщина льда  = 0,4 м. Плотность льда
= 0,4 м. Плотность льда  , с которой надо давить на поршень горизонтального цилиндра площадью основания
, с которой надо давить на поршень горизонтального цилиндра площадью основания 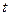 = 2,5 с выдавить из него через круглое отверстие площадью
= 2,5 с выдавить из него через круглое отверстие площадью  = 4 мм2 слой жидкости толщиной
= 4 мм2 слой жидкости толщиной  = 5 см. Плотность жидкости
= 5 см. Плотность жидкости  = 1,33 м, заполнен водой до отметки
= 1,33 м, заполнен водой до отметки  = 2,5 см у его основания струя, вытекающая из отверстия, падает на пол на расстоянии
= 2,5 см у его основания струя, вытекающая из отверстия, падает на пол на расстоянии 
 = 1 м до краев заполнен жидкостью. Пренебрегая вязкостью жидкости, определите, на какой высоте
= 1 м до краев заполнен жидкостью. Пренебрегая вязкостью жидкости, определите, на какой высоте  = 50 см от цилиндра.
= 50 см от цилиндра. = 6 см2 и
= 6 см2 и  = 12 см2. Плотность воды
= 12 см2. Плотность воды 
 = 1 м, если через отверстие диаметром
= 1 м, если через отверстие диаметром  = 0,5 см всплывает в широком сосуде в глицерине. Определите предельную скорость
= 0,5 см всплывает в широком сосуде в глицерине. Определите предельную скорость 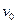 шарика, если течение жидкости, вызванное его всплытием, является ламинарным. Плотность материала шарика
шарика, если течение жидкости, вызванное его всплытием, является ламинарным. Плотность материала шарика  = 1,48 Па · с.
= 1,48 Па · с. молекул которого равна 8· 1025 м -3. Определите массу
молекул которого равна 8· 1025 м -3. Определите массу  = 3,1 МПа, находился на складе при температуре
= 3,1 МПа, находился на складе при температуре  = 6 °С. Израсходовав половину газа, баллон внесли в помещение. Определите температуру
= 6 °С. Израсходовав половину газа, баллон внесли в помещение. Определите температуру  в помещении, если давление газа через некоторое время стало
в помещении, если давление газа через некоторое время стало  = 1,6 МПа.
= 1,6 МПа. смеси.
смеси. после расширения; 3) плотность газа
после расширения; 3) плотность газа  молекул газа в сосуде.
молекул газа в сосуде. молекул идеального газа, плотность которого при давлении 35 кПа составляет 0,3 кг/м3.
молекул идеального газа, плотность которого при давлении 35 кПа составляет 0,3 кг/м3. газа, его объемом
газа, его объемом  поступательного движения всех молекул газа.
поступательного движения всех молекул газа. поступательного движения молекул, содержащихся в 1 моль
поступательного движения молекул, содержащихся в 1 моль  и в 1 кг
и в 1 кг  азота при температуре 300 К.
азота при температуре 300 К.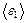 , приходящуюся на одну степень свободы молекулы кислорода, среднюю кинетическую энергию поступательного движения
, приходящуюся на одну степень свободы молекулы кислорода, среднюю кинетическую энергию поступательного движения  молекулы, среднюю кинетическую энергию вращательного движения
молекулы, среднюю кинетическую энергию вращательного движения  молекулы, среднее значение полной кинетической энергии
молекулы, среднее значение полной кинетической энергии  молекулы, а также среднюю кинетическую энергию вращательного движения
молекулы, а также среднюю кинетическую энергию вращательного движения  всех молекул газа. Газ считать идеальным, температура газа Т = 500 К, масса газа т = 10 г.
всех молекул газа. Газ считать идеальным, температура газа Т = 500 К, масса газа т = 10 г. газа.
газа. смеси газов, содержащей гелий массой т1 = 1 г и водород массой т2 — 2 г.
смеси газов, содержащей гелий массой т1 = 1 г и водород массой т2 — 2 г.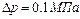 . Определите количество теплоты Q, сообщенное газу.
. Определите количество теплоты Q, сообщенное газу.
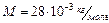 ) находится при температуре
) находится при температуре  . В результате изохорного охлаждения его давление уменьшилось в
. В результате изохорного охлаждения его давление уменьшилось в  раза, а затем в результате изобарного расширения температура газа в конечном состоянии оказалась равной первоначальной. Определите: 1)работу А, совершенную газом; 2) изменение внутренней энергии
раза, а затем в результате изобарного расширения температура газа в конечном состоянии оказалась равной первоначальной. Определите: 1)работу А, совершенную газом; 2) изменение внутренней энергии  до объема
до объема  . Работа А расширения газа равна 900 Дж. Определите наиболее вероятную скорость
. Работа А расширения газа равна 900 Дж. Определите наиболее вероятную скорость  молекул газа.
молекул газа. .Определите показатель политропы n этого процесса.
.Определите показатель политропы n этого процесса. удельная теплота парообразования воды
удельная теплота парообразования воды 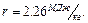
 моль совершает цикл, состоящий из двух изохор и двух изобар (см. рисунок). Определите работу А, совершенную газом за цикл, если точки 2 и 4 лежат на одной изотерме, начальная температура
моль совершает цикл, состоящий из двух изохор и двух изобар (см. рисунок). Определите работу А, совершенную газом за цикл, если точки 2 и 4 лежат на одной изотерме, начальная температура  газа равна 300 К, а температура Т 3 газа в результате изобарного расширения достигла 500 К.
газа равна 300 К, а температура Т 3 газа в результате изобарного расширения достигла 500 К.