
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механічних спеціальностей заочної форми навчання.Содержание книги
Поиск на нашем сайте
Укладачі: Сергій Іванович Куліков Діна Григорівна Іванова Галина Олександрівна Ткаченко
Редактор Л. М. Тонкошкур Коректор Л. Я. Гоцуцова
Підп. до друку 10. 12.2001. Формат 60х41/16. Папір друк. №2. Друк офсетний. Умовн. – друк. арк. 1,27. Облік. – видавн. арк. 1,27 Тираж 100 прим. Зам. №. УДХТУ, 49005, Дніпропетровськ – 5, пр. Гагаріна, 8 Дільниця оперативної поліграфії ІнКомЦентру УДХТУ
Методичні вказівки до виконання контрольної роботи № 3 з курсів “Обчислювальна математика, програмування і розрахунки на ЕОМ” та “Інформатика” для студентів технологічних і механічних спеціальностей заочної форми навчання складені відповідно до програми дисципліни і служать для надання методичної допомоги при виконанні контрольної роботи № 3 в освоєнні основних методів обчислень, край необхідних при виконанні розрахункових робіт у курсовому, дипломному проектуваннях з опрацювання експериментальних даних, обґрунтування і вибору оптимальних умов проведення технологічного процесу, а також при проведенні обчислень різноманітного призначення. Контрольна робота має п’ять завдань, що виконуються відповідно до індивідуального варіанта. Перше завдання – це обчислення систем нелінійних рівнянь, друге – розв’язання крайової задачі за методом скінчених різниць або прогонки, третє – знаходження інтервальної оцінки параметрів нормально розподіленої випадкової величини: математичного сподівання, дисперсії і знаходження надійних інтервалів до них, четверте завдання – зробити оцінку впливу фактора X на величину Y, п’яте завдання – обчислити рівняння регресії і зробити перевірку його на адекватність експериментальним даним. Для правильного вибору індивідуального варіанта завдань необхідно обчислити два параметри: N і К. Ці параметри визначаються за шифром студента. Параметр N – це сума трьох останніх цифр шифру, а параметр К – сума двох останніх цифр шифру. Наприклад: шифр студента – 91135, тоді N=1+3+5=9, К=3+5=8. Якщо виявиться, що N=0, то прийняти N=20, а якщо К=0, то прийняти К=20. Контрольна робота оформляється у звичайному зошиті у клітинку акуратним і розбірливим почерком. Кожне завдання треба починати з написання умов обчислень. Всі розрахунки робляться за допомогою калькулятора.
До усіх завдань приводяться приклади з повними і докладними розрахунками. Контрольну роботу необхідно виконати і здати її у деканат до початку екзаменаційної сесії. Це забезпечить своєчасну її перевірку. Роботи, виконані вірно, одержують позитивну рецензію і допускаються до захисту. Захист робіт здійснюється на екзаменаційній сесії за розкладом. Контрольні роботи, виконані з помилками, до захисту не допускаються і доопрацьовуються до моменту одержання позитивної рецензії. Чисельне розв’язання систем нелінійних рівнянь Для обчислення систем нелінійних рівнянь можна вживати метод Ньютона або метод простої ітерації. Метод Ньютона Задано систему нелінійних рівнянь:
Необхідно знайти корені системи. Згідно методу Ньютона послідовність наближень обчислюється за формулами:
де Матрицею Якобі є матриця, складена з часткових похідних правих частин системи:
Початкове наближення Умови завершення ітераційного процесу:
де
Метод Ньютона має ефект при достатній близькості початкового наближення до кінцевого результату обчислення. Приклад 1.1. Розв’язати систему нелінійних рівнянь:
Початкові наближення коренів З першого рівняння системи одержуємо
Побудуємо таблицю і графік обох залежностей:
Таблиця 1.1
Мал. 1.1 Згідно графіка (мал. 1.1) наближені значення: Обчислюємо Якобіан у точці
За формулами (1.1) одержуємо
Далі підставляємо у формули (1.1) одержані
Метод простої ітерації Задано систему нелінійних рівнянь:
Необхідно знайти корені цієї системи з заданою точністю. Для вживання метода простої ітерації система (1.4) приводиться до виду:
Складаємо матрицю Якобі
і обчислюємо першу або другу норми матриці (перша норма – це максимальна сума модулів елементів матриці по рядкам, а друга норма – це максимальна сума модулів елементів матриці по стовпцям):
Якщо будь-яка із норм матриці буде менше одиниці, то ітераційний процес буде збіжним. Розв’язування визначається за формулами:
де Оцінка похибки n – го наближення дається нерівністю:
де
Приклад 1.2. Розв’язати систему нелінійних рівнянь і дати оцінку похибки результату:
З першого рівняння системи (1.11) одержуємо
Побудуємо таблицю і графік обох залежностей. Згідно графіка корені системи (1.11) знаходяться в області
Складемо матрицю Якобі:
Таблиця 1.2
Мал. 1.2 Оскільки Якщо беремо нульові наближення коренів
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.107.148 (0.01 с.) |

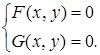
 (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3) і
і  знаходять за графіком.
знаходять за графіком. (1.4)
(1.4) – наступні наближення коренів
– наступні наближення коренів  та
та  ;
; – попередні наближення коренів
– попередні наближення коренів  – задана точність розв’язання системи рівнянь.
– задана точність розв’язання системи рівнянь.

 та
та  знайдемо графічним способом.
знайдемо графічним способом. , а з другого
, а з другого  :
:


 :
:


 і
і  , потім
, потім  і
і  і так до тих пір, доки не буде досягнута задана точність
і так до тих пір, доки не буде досягнута задана точність  (виконаються умови (1.4)).
(виконаються умови (1.4)). (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7) (1.8)
(1.8) , (1.9)
, (1.9) , (1.10)
, (1.10) і
і  – точне рішення системи (1.4);
– точне рішення системи (1.4); .
. (1.1)
(1.1) , а з другого –
, а з другого –  :
:
 ;
;  ; нехай
; нехай  ;
;  . Перетворимо систему рівнянь (1.11) до вигляду:
. Перетворимо систему рівнянь (1.11) до вигляду:
 .
.
 і
і  , то будь-яка норма матриці Якобі буде менше 1, отже ітераційний процес у досліджувальній області буде мати збіжність.
, то будь-яка норма матриці Якобі буде менше 1, отже ітераційний процес у досліджувальній області буде мати збіжність. 1,8, тоді
1,8, тоді


 Отже можна вважати, що розв’язування знайдене з точністю до 0,012. Відповідь
Отже можна вважати, що розв’язування знайдене з точністю до 0,012. Відповідь  .
.


