
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Український державний хіміко-технологічний університетСодержание книги
Поиск на нашем сайте
УКРАЇНСЬКИЙ ДЕРЖАВНИЙ ХІМІКО-ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ КОНТРОЛЬНОЇ РОБОТИ № 3 З КУРСІВ “ОБЧИСЛЮВАЛЬНА МАТЕМАТИКА, ПРОГРАМУВАННЯ І РОЗРАХУНКИ НА ЕОМ” ТА “ІНФОРМАТИКА” ДЛЯ СТУДЕНТІВ ТЕХНОЛОГІЧНИХ І МЕХАНІЧНИХ СПЕЦІАЛЬНОСТЕЙ ЗАОЧНОЇ ФОРМИ НАВЧАННЯ
Дніпропетровськ УДХТУ 2005
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ УКРАЇНСЬКИЙ ДЕРЖАВНИЙ ХІМІКО-ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ КОНТРОЛЬНОЇ РОБОТИ № 3 З КУРСІВ “ОБЧИСЛЮВАЛЬНА МАТЕМАТИКА, ПРОГРАМУВАННЯ І РОЗРАХУНКИ НА ЕОМ” ТА “ІНФОРМАТИКА” ДЛЯ СТУДЕНТІВ ТЕХНОЛОГІЧНИХ І МЕХАНІЧНИХ СПЕЦІАЛЬНОСТЕЙ ЗАОЧНОЇ ФОРМИ НАВЧАННЯ
Затверджено на засіданні кафедри ОТ та ПМ Протокол № 4 від 16.12.04
Дніпропетровськ УДХТУ 2005
Методичні вказівки до виконання контрольної роботи № 3 з курсів “Обчислювальна математика, програмування і розрахунки на ЕОМ” та “Інформатика” для студентів технологічних і механічних спеціальностей заочної форми навчання – Дніпропетровськ: УДХТУ, 2005. – 22с.
Укладачі: С. І. Куліков Д. Г. Іванова Г. О. Ткаченко
Відповідальний за випуск С. І. Куліков
Навчальне видання Методичні вказівки до виконання контрольної роботи № 3 З курсів “Обчислювальна математика, програмування і розрахунки на ЕОМ” та “Інформатика” для студентів технологічних і Чисельне розв’язання систем нелінійних рівнянь Для обчислення систем нелінійних рівнянь можна вживати метод Ньютона або метод простої ітерації. Метод Ньютона Задано систему нелінійних рівнянь:
Необхідно знайти корені системи. Згідно методу Ньютона послідовність наближень обчислюється за формулами:
де Матрицею Якобі є матриця, складена з часткових похідних правих частин системи:
Початкове наближення Умови завершення ітераційного процесу:
де
Метод Ньютона має ефект при достатній близькості початкового наближення до кінцевого результату обчислення.
Приклад 1.1. Розв’язати систему нелінійних рівнянь:
Початкові наближення коренів З першого рівняння системи одержуємо
Побудуємо таблицю і графік обох залежностей:
Таблиця 1.1
Мал. 1.1 Згідно графіка (мал. 1.1) наближені значення: Обчислюємо Якобіан у точці
За формулами (1.1) одержуємо
Далі підставляємо у формули (1.1) одержані
Метод простої ітерації Задано систему нелінійних рівнянь:
Необхідно знайти корені цієї системи з заданою точністю. Для вживання метода простої ітерації система (1.4) приводиться до виду:
Складаємо матрицю Якобі
і обчислюємо першу або другу норми матриці (перша норма – це максимальна сума модулів елементів матриці по рядкам, а друга норма – це максимальна сума модулів елементів матриці по стовпцям):
Якщо будь-яка із норм матриці буде менше одиниці, то ітераційний процес буде збіжним. Розв’язування визначається за формулами:
де Оцінка похибки n – го наближення дається нерівністю:
де
Приклад 1.2. Розв’язати систему нелінійних рівнянь і дати оцінку похибки результату:
З першого рівняння системи (1.11) одержуємо
Побудуємо таблицю і графік обох залежностей. Згідно графіка корені системи (1.11) знаходяться в області
Складемо матрицю Якобі:
Таблиця 1.2
Мал. 1.2 Оскільки Якщо беремо нульові наближення коренів
Метод кінцевих різниць Нехай Система рівновіддалених вузлів з деяким кроком
а на кінцях інтервалу (для крайніх точок) призначимо:
Використовуючи ці формули замінимо рівняння (2.1) та крайові умови (2.2) складеною системою рівнянь:
Одержимо лінійну алгебраїчну систему Приклад 2.1. Обчислити лінійну крайову задачу:
Тут
Розіб’ємо відрізок Обчислення крайової задачі звелось до знаходження чотирьох значень функції Для знаходження чотирьох невідомих треба скласти і обчислити систему із чотирьох рівнянь:
Зробивши тотожні перетворювання (зведення до спільного знаменника і зведення подібних членів) і підставивши
Розв’язуючи систему (2.3) Таблиця 2.1
одержимо обчислення крайової задачі (табл.. 2.1).
Метод прогонки Усі обчислення у методі прогонки діляться на дві частини: прямий хід і зворотний хід. Результати обчислень зручно записувати до таблиці. При прямому ході заповнюють усі колонки таблиці (окрім останньої) зверху донизу. При зворотному ході заповнюється остання колонка таблиці знизу догори. Обчислювальні формули мають вигляд:
Обчислення проводяться у такому порядку: Прямий хід. Знайдемо Зворотний хід. Обчислимо значення Приклад 2.2. За методом прогонки розв’язати крайову задачу:
За формулами (2.5) обчислюємо:
Пам’ятаючи, що
Обчислюємо за формулами (2.4):
За формулами (2.6) обчислюємо:
Аналогічно обчислюються При зворотному ході спочатку обчислюється Усі обчислені дані заносяться у таблицю. Таблиця 2.2
Якщо у краєвих умовах
Приклад 3.1. За заданою вибіркою значень випадкової величини знайти оцінки математичного сподівання, дисперсії і надійні інтервали до них. Оцінити нормальність розподілу. Розглянемо варіант для K=30, N=1. Результати обчислень наведені у таблиці 3.1.
Таблиця 3.1
Так як Зробимо оцінку надійних інтервалів до математичного сподівання і дисперсії.
Якщо
Надійний інтервал для математичного Критерій Стьюдента
сподівання –
З таблиці 3.3 для
Таблиця 3.3 Критерій
Таким чином, надійний інтервал для дисперсії –
Приклад 4.1. Дати оцінку дії фактора Результати експерименту подано Таблиця 4.2
у таблиці 4.2. 1. Обчислюємо
аналогічно знаходимо 2. Обчислюємо загальне середнє
3. Обчислюємо дисперсію фактора
4. Знаходимо табличне значення Таблиця 4.3 критерію Фішера для
5. Обчислюємо розрахункове значення критерію Фішера:
фактор
Приклад 5.1. Знайти рівняння регресії і перевірити його на адекватність. Складаємо таблицю. Таблиця 5.1
Вихідні дані беремо з прикладу (4.1) табл. (4.2). Обчислюємо з першого по п’ятий рядок За даними таблиці складаємо систему рівнянь (5.1):
Обчислюємо
Підставляємо у рівняння (5.2) значення
Обчислюємо критерій Фішера:
Критерій Фішера табличний (табл.4.3):
Список літератури 1. Брановицкая С. В., Медведев Р. Б., Фиалков Ю. Я. Вычислительная математика в химии и химической технологии. – Киев: Головне видавництво “Вища школа”, 1986. – 216 с.
2. Волков Е. А. Численные методы. Учебное пособие для ВУЗов. – 2-е изд., испр. – М.: Наука, 1987. – 248 с. 3. Гаврилюк І. П., Макаров В. Л. Методи обчислень. Підручник у 2 ч. – К.: Вища школа, 1995. – 4 ч. – 431 с. 4. Ляшенко М. С., Головань М. С. Чисельні методи: Підручник. – К.: Либідь, 1996. – 288 с. 5. Демидович В. П., Марон И. А. Основы вычислительной математики. – М.: Наука, 1976. – 664 с. 6. Калиткин Н. Н. Численные методы: Учебное пособие. – М.: Наука, 1976. – 503 с. 7. Копченова Н. В., Марон И. А. Основы вычислительной математики в примерах и задачах. – М.: Наука, 1972. – 357 с.
Зміст Стор.
1. Введення............................................................................................................3 2. Чисельні рішення систем нелінійних рівнянь...............................................4 3. Варіанти індивідуальних завдань...................................................................7 4. Розв’язування лінійної крайової задачі..........................................................7 5. Варіанти індивідуальних завдань.................................................................12 6. Інтервальна оцінка параметрів нормально розподіленої випадкової величини...............................................................12 7. Варіанти індивідуальних завдань.................................................................15 8. Дисперсійний аналіз......................................................................................15 9. Варіанти індивідуальних завдань.................................................................17 10. Регресійний аналіз..........................................................................................18 11. Варіанти індивідуальних завдань.................................................................20 12. Список літератури..........................................................................................21 13. Зміст.................................................................................................................22 УКРАЇНСЬКИЙ ДЕРЖАВНИЙ ХІМІКО-ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ МЕТОДИЧНІ ВКАЗІВКИ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.4.99 (0.009 с.) |

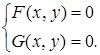
 (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3) і
і  знаходять за графіком.
знаходять за графіком. (1.4)
(1.4) – наступні наближення коренів
– наступні наближення коренів 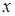 та
та  ;
; – попередні наближення коренів
– попередні наближення коренів  – задана точність розв’язання системи рівнянь.
– задана точність розв’язання системи рівнянь.

 та
та  знайдемо графічним способом.
знайдемо графічним способом. , а з другого
, а з другого  :
:


 :
:


 і
і  , потім
, потім  і
і  і так до тих пір, доки не буде досягнута задана точність
і так до тих пір, доки не буде досягнута задана точність  (виконаються умови (1.4)).
(виконаються умови (1.4)). (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7) (1.8)
(1.8) , (1.9)
, (1.9) , (1.10)
, (1.10) і
і  – точне рішення системи (1.4);
– точне рішення системи (1.4); .
. (1.1)
(1.1) , а з другого –
, а з другого –  :
:
 ;
;  ; нехай
; нехай  ;
;  . Перетворимо систему рівнянь (1.11) до вигляду:
. Перетворимо систему рівнянь (1.11) до вигляду:
 .
.
 і
і  , то будь-яка норма матриці Якобі буде менше 1, отже ітераційний процес у досліджувальній області буде мати збіжність.
, то будь-яка норма матриці Якобі буде менше 1, отже ітераційний процес у досліджувальній області буде мати збіжність. 1,8, тоді
1,8, тоді


 Отже можна вважати, що розв’язування знайдене з точністю до 0,012. Відповідь
Отже можна вважати, що розв’язування знайдене з точністю до 0,012. Відповідь  .
. .
. , та
, та  . Позначимо у результаті обчислення наближені значення функції
. Позначимо у результаті обчислення наближені значення функції  та її похідних
та її похідних  у вузлах
у вузлах  через
через  відповідно. Замінимо у кожному внутрішньому вузлі похідні
відповідно. Замінимо у кожному внутрішньому вузлі похідні  і
і  кінцево-різничними відношеннями (для внутрішніх точок):
кінцево-різничними відношеннями (для внутрішніх точок): ,
, .
.
 рівнянь з
рівнянь з 



 на частини з кроком
на частини з кроком  ; одержимо чотири вузлові точки. Дві з них
; одержимо чотири вузлові точки. Дві з них  називаються межовими, а дві інші
називаються межовими, а дві інші  та
та  – внутрішніми.
– внутрішніми. , відповідно значенням аргументів
, відповідно значенням аргументів  .
. =1;
=1; ;
; ;
; .
. , одержимо
, одержимо (2.3)
(2.3)
 (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8) та
та  (2.5). За формулами (2.4) обчислимо значення
(2.5). За формулами (2.4) обчислимо значення  . За допомогою рекурентних формул (2.6) обчислимо
. За допомогою рекурентних формул (2.6) обчислимо  та
та  .
. за формулою (2.7). Застосовуючи формулу (2.8), одержимо інші значення
за формулою (2.7). Застосовуючи формулу (2.8), одержимо інші значення 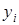 , починаючи з
, починаючи з  .
.


 до
до  з кроком 0,1
з кроком 0,1 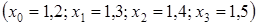 , одержимо:
, одержимо:


 , які необхідно одержати при прямому ході.
, які необхідно одержати при прямому ході. за формулою (2.7), а потім
за формулою (2.7), а потім  та
та 


 , то
, то  , а
, а  .
.













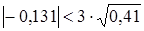 і
і  , то вибірковий закон розподілу можна вважати нормальним.
, то вибірковий закон розподілу можна вважати нормальним. і
і  то
то  ; із таблиці 3.2 знаходимо критерій Стьюдента
; із таблиці 3.2 знаходимо критерій Стьюдента  , тоді
, тоді . Таблиця 3.2
. Таблиця 3.2 :
:

 знайдемо
знайдемо 




 :
: .
.


 і записуємо їх у таблицю.
і записуємо їх у таблицю. (4.2):
(4.2):
 і дисперсію помилки
і дисперсію помилки 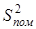 (4.1):
(4.1):


 для рівня значимості
для рівня значимості 








 і по стовпцям обчислюємо їх суми.
і по стовпцям обчислюємо їх суми.
 складаємо рівняння регресії:
складаємо рівняння регресії: (5.2)
(5.2)

 ; оскільки
; оскільки  , то рівняння адекватне експериментальним даним.
, то рівняння адекватне експериментальним даним.


