
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сумма квадрата тангенса угла и единицы равна единице, деленной на квадрат косинуса этого угла.Содержание книги
Поиск на нашем сайте
Основы тригонометрии. Обобщение понятия угла
Ð AOB = a, 0 ° £ a £ 180 °.
Рассмотрим в ОА - начальный радиус
Ð (ОА, Описание: Углом поворота AOМ называется угол, образованный вращением вокруг начала координат начального радиуса ОА до положения ОМ.
a1 = Ð AOМ 1 = 45° a2 = Ð AOМ 2 = - 45°
Если начальный радиус повернуть против часовой стрелки на 180°, а потом еще на 30°, то угол поворота будет равен 210°. И начальный радиус сделает полный оборот, то угол поворота будет равен 360°, если он сделает полтора оборота в том же направлении, то угол поворота будет равен 540° и так далее.
Вывод: Угол поворота может принимать любые значения, большие 360° и меньшие - 360°.
Упражнение: Постройте углы 405°, - 210°, 840°, - 1320°, 2385°. Рассмотрим в Вопрос: Какие углы будут соответствовать этому же радиус-вектору? Ответ: Если a = Ð AOМ = 150°, то углы 150° + 360° n, где n Î Z, соответствуют этому же радиус-вектору. При n= 0, 1, - 1, 2, - 2 получаем 150°, 510°, - 210°, 870°, -570°.
Вывод: Радиус-вектору Замечание: Пусть при повороте на угол a начальный радиус ОА переходит в положение Если a Î (0°; 90°), то a+ 360° n, где n Î Z, - углы 1-ой координатной четверти. Если a Î (90°; 180°), то a+ 360° n, где n Î Z, - углы 2-ой координатной четверти. Если a Î (180°; 270°), то a+ 360° n, где n Î Z, - углы 3-ей координатной четверти. Если a Î (270°; 360°), то a + 360° n, где n Î Z, - углы 4-ой координатной четверти. Углы 0º, ± 90º, ± 180º, ± 270º, ± 360º, … не принадлежат никакой координатной четверти. Пример: Какой координатной четверти принадлежит угол - 2763 °? Решение: Разделив 2763° на 360°, выясним, сколько полных оборотов нужно сделать при построении данного угла. - 2763 ° = - 360° · 7 - 243°. Так как угол - 243° принадлежит 2-ой к. ч., значит, угол - 2763 ° принадлежит 2-ой к. ч. Ответ: - 2763 ° Î 2-ой к. ч. Упражнение: Какой координатной четверти принадлежат углы: 598°, 3672°, - 1743°?
2. Градусная и радианная меры угла
 часть одного полного оборота. часть одного полного оборота.
Рассмотрим в a = Ð A 1 O В 1= Ð A 2 O В 2 Углу a соответствует дуга l1 = A1 М1 В1 Для данного центрального угла a отношение длины дуги к длине радиуса есть величина постоянная.
Определение: Число а, равное отношению длины дуги l, соответствующей некоторому центральному углу a, к длине радиуса r, называется радианной мерой этого угла. Вывод: Если радиус окружности равен 1, то радианная мера центрального угла – это длина дуги, соответствующей этому центральному углу.
Определение: 1 радиан – единица радианной меры угла – это центральный угол, которому соответствует дуга, равная радиусу.
Всякий угол, заданный в градусной мере, можно перевести в радианную меру, и, наоборот, угол, заданный в радианной мере, можно перевести в градусную меру. Углу 360° соответствует дуга, равная длине окружности (lокр. = 2p r).
a – градусная мера данного угла; а – радианная мера данного угла.
3.
Рассмотрим в На ОА - начальный радиус
Ð (ОА, ОМ) = Ð AO М = a. Определение: Синусом угла a называется ордината радиус-вектора точки М, принадлежащей
Определение: Косинусом угла a называется абсцисса радиус-вектора точки М, принадлежащей
Определение: Тангенсом угла a называется отношение ординаты радиус-вектора точки М, принадлежащей
Определение: Котангенсом угла a называется отношение абсциссы радиус-вектора точки М, принадлежащей
С изменением угла a координаты радиус-вектора точки
Функции Вывод: Функция Функция Вывод: 1) 2) Замечание: 1) Углы
 , называют углами горизонтального диаметра (Рис.2). , называют углами горизонтального диаметра (Рис.2).
Рис.1. Рис.2. 4. Знаки тригонометрических функций Так как
Вывод:
Так как Вывод:
Так как В 1-ой и 3-ей к. ч. x и y имеют одинаковые знаки, а во 2-ой и 4-ой к. ч. x и y имеют разные знаки. Вывод:
Пример: Определить знак выражения: 1) sin 973º; 2) Решение: 1) 973º = 360º·2 + 253º; 253ºÎ (180°; 270°), значит, 973ºÎ 3-ей к. ч., следовательно, sin 973º < 0. 2) следовательно, Ответ: sin 973º < 0; Упражнения: №1. Среди углов 770º, 480º, – 50º, 1560º, – 240º, – 310º найдите такие углы, при которых начальный радиус займет то же положение, что и при повороте на угол: а) a = 50º; б) a = 120º. №2. Определите знак выражения: cos 567º; sin 5791º; tg 269º; ctg (– 705º); cos 1259º; ctg №3. Какой знак имеют
№4. Определите знак выражения: а) sin 190º · tg 200º; б) cos 320º · ctg 79º; в) cos 271º · sin 453º · tg 514º · ctg 378º, г) – sin 50º ·(– cos (– 91º)) · tg 170º· ctg (– 640º) · sin 530º. №5. Углом какой координатной четверти является угол a, если: а) sin a > 0 и cos a > 0; г) sin a > 0 и tg a > 0; б) sin a < 0 и cos a > 0; д) tg a < 0 и cos a > 0; в) sin a < 0 и cos a < 0; е) ctg a > 0 и sin a < 0. 5. Значения тригонометрических функций основных углов.
  . .
Воспользуемся определениями тригонометрических функций для нахождения значений тригонометрических функций основных углов. Основные углы:
Радиус-вектор
sin 0º = sin 360º = y = 0; cos 0º = cos 360º = x = 1; tg 0º = tg 360º = Радиус-вектор sin 90º = y = 1; cos 90º = x = 0; tg 90º = Радиус-вектор sin 180º = y = 0; cos 180º = x = –1; tg 180º = Радиус-вектор sin 270º = y = –1; cos 270º = x = 0;
 – не существует; ctg 270º = – не существует; ctg 270º =  = 0 = 0
Рис.1. a = 30º. Рис.2. a = 60º. Рис.3. a = 45º.
Рис.1. Радиус-вектор sin 30º = y = Рис.2. Радиус-вектор sin 60º = y = Рис.3. Радиус-вектор sin 45º = y = Пример:
№1. Вычислить значения всех тригонометрических функций углов: a)
 ; ;
b) a2 = 225º c) a3 = 330º Решение: a) Радиус-вектор Радиус-вектор sin 120º = y = b)Радиус-вектор Радиус-вектор sin 225º = y = c) Радиус-вектор Радиус-вектор sin 330º = y = №2. Для каких значений угла верно равенство: 1) cos b = 0; 2) Решение:
 a + a +  = =  + 2 p k, k Î Z + 2 p k, k Î Z
a =
a = - p + 2p k, k Î Z a = p + 2p k, k Î Z b = Ответ: 1) b = №3. Найти область допустимых значений аргумента a: Решение: 1) Исключаем значения a, при которых не существует ctg a: a ¹ p k, k Î Z. 2) Исключаем значения a, при которых знаменатель дроби sin a +1 обращается в нуль: sin a +1 ¹ 0; sin a ¹ – 1; a ¹ Ответ:a ¹ p k, k Î Z; a ¹ Упражнения: №1. Вычислить значения всех тригонометрических функций углов: 135º №2. Найти значение выражения: а) 2 sin p – 2 cos в) 3 sin 2 д) №3. Для каких значений углаверно равенство: а) sin a = 1; б) cos b = – 1; в) tg a = 0; г) ctg b =1. 6. Изменение тригонометрических функций с увеличением угла. Рассмотрим в ОА - начальный радиус окр. (О, r =1).
Ð (ОА, ОМ) = a.
Проследим за изменением каждой из четырех тригонометрических функций в отдельности при изменении угла a от 0º до 360º.
sin a ведет себя как ордината y радиус-вектора точки М, принадлежащей окр. (О, r =1). (Рис. 1.) Если a Î (0°; 90°), то Если a Î (90°; 180°), то Если a Î (180°; 270°), то Если a Î (270°; 360°), то Вывод: 1. 2. 3.
Рис. 1. Рис. 2.
(Рис. 2.) Если a Î (0°; 90°), то cos a уменьшается от 1 до 0. Если a Î (90°; 180°), то cos a уменьшается от 0 до – 1. Если a Î (180°; 270°), то cos a увеличивается от – 1 до 0. Если a Î (270°; 360°), то cos a увеличивается от 0 до 1.
Вывод: 1. 2. 3.
Через конец начального радиуса ОА точку А проведем ось АТ, параллельную оси Оу. Радиус-вектор точке N. Алгебраическая величина отрезка АN равна tg a, где a – угол любой из четырех координатных четвертей (Рис. 1).
Рис.1. Рис.2.
Если a Î (0°; 90°), то tg a = АN возрастает от 0 до + ¥ при увеличении угла a. Если a Î (90°; 180°), то tg a = АN возрастает от – ¥ до 0 при увеличении угла a. Если a Î (180°; 270°), то tg a = АN возрастает от 0 до + ¥ при увеличении угла a. Если a Î (270°; 360°), то tg a = АN возрастает от – ¥ до 0 при увеличении угла a. Вывод: 1. 2. 3.
Так как дроби |

 . На
. На  - радиус-вектор точки М, принадлежащей
- радиус-вектор точки М, принадлежащей  .
. . Построим угол a = Ð AO М = 150°.
. Построим угол a = Ð AO М = 150°. , дуга l2 = A2 М2 В2
, дуга l2 = A2 М2 В2  .
.
 ;
; 

 ; 360° = 2p; 180 ° = p.
; 360° = 2p; 180 ° = p.
 выберем точку М (x; y).
выберем точку М (x; y). .
.  .
.



 меняются, а его модуль остается без изменения.
меняются, а его модуль остается без изменения.  ,
,  ,
,  ,
,  – переменные величины, зависящие от a. Каждому допустимому значению a соответствует единственное значение
– переменные величины, зависящие от a. Каждому допустимому значению a соответствует единственное значение  , так как для любого угла поворота можно найти значения координат y и x.
, так как для любого угла поворота можно найти значения координат y и x.
 ;
; 
 имеет смысл при любом
имеет смысл при любом  , ±
, ±  , ±
, ±  , …, так как для этих углов не имеет смысла дробь
, …, так как для этих углов не имеет смысла дробь  (x = 0).
(x = 0). имеет смысл при любом
имеет смысл при любом  (y = 0).
(y = 0).



 , называют углами вертикального диаметра (Рис.1).
, называют углами вертикального диаметра (Рис.1). , то знак
, то знак  , если a является углом 1-ой или 2-ой координатных четвертей,
, если a является углом 1-ой или 2-ой координатных четвертей, , если a является углом 3-ей или 4-ой координатных четвертей.
, если a является углом 3-ей или 4-ой координатных четвертей. , то знак
, то знак  зависит от знака абсциссы x. В 1-ой и 4-ой координатных четвертях x > 0, во 2-ой и 3-ей координатных четвертях x < 0.
зависит от знака абсциссы x. В 1-ой и 4-ой координатных четвертях x > 0, во 2-ой и 3-ей координатных четвертях x < 0. , если a является углом 1-ой или 4-ой координатных четвертей,
, если a является углом 1-ой или 4-ой координатных четвертей, , если a является углом 2-ой или 3-ей координатных четвертей.
, если a является углом 2-ой или 3-ей координатных четвертей. и
и  , то знаки
, то знаки  ,
,  , если a является углом 1-ой или 3-ей к. ч.,
, если a является углом 1-ой или 3-ей к. ч., ,
,  , если a является углом 2-ой или 4-ой к. ч.
, если a является углом 2-ой или 4-ой к. ч.

 .
.
 Î 4-ой к. ч., значит,
Î 4-ой к. ч., значит,  Î 4-ой к. ч.,
Î 4-ой к. ч., .
. .
. .
. ,
,  ,
,  ,
,  , если:
, если: .
.













 , образующий углы 0º и 360º, имеет координаты (1; 0).
, образующий углы 0º и 360º, имеет координаты (1; 0). = 0; ctg 0º = ctg 360º =
= 0; ctg 0º = ctg 360º = 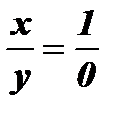 – не существует.
– не существует. ,образующий угол 90º, имеет координаты (0; 1).
,образующий угол 90º, имеет координаты (0; 1). ,образующий угол 180º, имеет координаты (– 1; 0).
,образующий угол 180º, имеет координаты (– 1; 0). ,образующий угол 270º, имеет координаты (0; – 1).
,образующий угол 270º, имеет координаты (0; – 1).


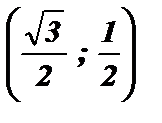 .
. ; cos 30º = x =
; cos 30º = x =  ; tg 30º =
; tg 30º =  =
=  ; ctg 30º =
; ctg 30º =  =
=  .
.
 ; cos 60º = x =
; cos 60º = x =  ; tg 60º =
; tg 60º =  =
=  ; ctg 60º =
; ctg 60º =  =
=  .
.
 ; cos 45º = x =
; cos 45º = x =  ; tg 45º =
; tg 45º =  = 1; ctg 45º =
= 1; ctg 45º =  = 1.
= 1.




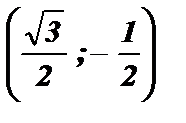
 ;
; .
. , соответствующий углу a = 60º, имеет координаты
, соответствующий углу a = 60º, имеет координаты 
 , соответствующий углу a =120º, имеет координаты
, соответствующий углу a =120º, имеет координаты 
 ; cos 120º = x =
; cos 120º = x =  ; tg 120º =
; tg 120º =  =
=  ; ctg 120º =
; ctg 120º =  =
= 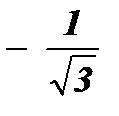 .
. , соответствующий углу a = 45º, имеет координаты
, соответствующий углу a = 45º, имеет координаты  .
. , соответствующий углу a =225º, имеет координаты
, соответствующий углу a =225º, имеет координаты 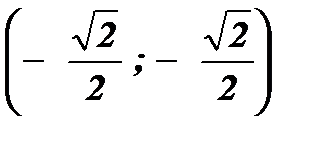 .
. ; cos 225º = x =
; cos 225º = x =  ; tg 225º =
; tg 225º =  = 1; ctg 225º =
= 1; ctg 225º =  = 1.
= 1.
 , соответствующий углу a=330º, имеет координаты
, соответствующий углу a=330º, имеет координаты  .
. ; cos 330º = x =
; cos 330º = x =  ; tg 330º =
; tg 330º =  =
=  ; ctg 330º =
; ctg 330º =  =
=  .
. .
. –
–  + 2 p k, k Î Z
+ 2 p k, k Î Z + p k, k Î Z
+ p k, k Î Z .
. + 2 p k, k Î Z
+ 2 p k, k Î Z + 2 p k, k Î Z.
+ 2 p k, k Î Z. ; 150º
; 150º  ; 210º
; 210º  ; 240º
; 240º 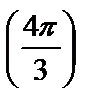 ; 300º
; 300º  ; 315º
; 315º  .
. +3 tg
+3 tg  – ctg
– ctg  ; б) cos 2
; б) cos 2  – cos 2
– cos 2  – 4 tg 2
– 4 tg 2  ;
; ; е)
; е)  .
.
 , то есть
, то есть  – множество значений
– множество значений  .
.
 , то есть
, то есть  – множество значений
– множество значений 

 , то есть
, то есть  – множество значений
– множество значений  .
.
 и
и  взаимно обратны, следовательно,
взаимно обратны, следовательно,  и
и 


