
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порівняння результатів експериментальних та теоретичних дослідженьСодержание книги
Поиск на нашем сайте
12. Запишіть висновки за результатами виконання лабораторної роботи. Контрольні запитання до лабораторної роботи 1. Дайте визначення складному напруженому стану позацентрового розтягування. 2. Що називають ядром перерізу і які його властивості? 3. Чим пояснюється спрощення формули (10.31) до вигляду (10.32) в умовах даного досліду? 4. Що називається ексцентриситетом приклдання сили e? Як його визначити? 5. Як визначити граничне навантаження зони пропорційності? Навіщо це потрібно? 6. Як змінюється несуча здатність стрижня при виникненні позацентрового стискування? 7. Які заходи вживаються по боротьбі з явищем позацентрового розтягування (стискування)? 8. Чому в експерименті використовуються два тензометри одночасно? 9. Наведіть приклади позацентрового розтягування (стискування) стрижнів у будівництві. 10. Чим викликана необхідність прикладення розтягуючих сил на достатньому віддалені від місця вимірювання деформацій?
ЛАБОРАТОРНА РОБОТА № 11 ДОСЛІДЖЕННЯ ЯВИЩА ВТРАТИ СТІЙКОСТІ СТИСНУТОГО СТРИЖНЯ Мета роботи: експериментально дослідити явище втрати стійкості під час осьового стискування гнучких стрижнів; порівняти значення критичних сил, що визначені за розрахунковими формулами і експериментально, за різних способів закріплення кінців стрижня. Обладнання: установка для експериментального визначення критичної сили. Загальні відомості Для багатьох елементів конструкцій і споруд розрахунки на міцність і жорсткість часто не достатні, щоб мати повну уяву про їхню робочу здатність, щоб з’ясувати, чи знаходиться конструкція або її частина в стані стійкої рівноваги. Розглянемо випадки втрати стійкості стрижнями, що найчастіше зустрічаються. Нехай прямолінійний стрижень стискується центральною силою P (рис. 2.17). На початку зростання цієї сили стрижень тільки скорочується, зберігаючи прямолінійну форму. При збільшенні сили настає втрата прямолінійної форми – стрижень згинається. Найменша центрально прикладена стискуюча сила, яка виводить стрижень із прямолінійної стійкої рівноваги, називається критичною силою Втрата стійкості стиснутого прямолінійного стрижня інколи називається поздовжнім згинанням, так як під дією поздовжніх сил стрижень викривлюється.
Рис. 2.17. Схема центрального стискування стрижня Поява поздовжнього згинання небезпечна сильним зростанням прогинів за незначного збільшення стискуючої сили. Зростання прогинів викликає швидке зростання напружень від згинання, які в свою чергу призводять до збільшення деформацій і часто спричинюють руйнування стрижня. У практиці відомі випадки, коли через втрату стійкості окремих стрижнів руйнувалися мости та інші споруди. Тому визначення критичних навантажень вважається відповідальною частиною інженерних розрахунків конструкцій. Теоретичне значення критичної сили визначається за формулою Ейлера:
де Е – модуль поздовжньої пружності матеріалу стрижня;
Рис. 2.18. Основні типи стиснутих стрижнів Критичні напруження, що виникають у момент втрати стійкості, визначаються так:
де Формули (2.37) і (2.38) справедливі лише тоді, коли напруження
Звідси можна визначити граничну гнучкість стрижня, яка є найменшим значенням гнучкості, при якому застосовується формула Ейлера:
Для звичайної будівельної сталі 3 - Опис установки Схема установки для експериментального визначення критичної сили зображена на рис. 2.19, а. Стрижень 2 завантажується за допомогою важільного механізму 6, який дозволяє створювати необхідну стискуючу силу вагою гир. Вага довгого важеля 6 з піддоном 8 врівноважується противагою 5. Тиск від гир, покладених на піддон 8, передається важелем 6 через шарнір 4 на верхній кінець стрижня 2, закріпленого у верхньому затисному пристрої 3. Нижній кінець стрижня установлено у нижньому затисному пристрої 1, прикріпленому до рами 9. Конструкція нижнього затисного пристрою 1 показана на рис. 2.19, б. Цей пристрій забезпечує шарнірне та жорстке опирання стрижня 2. Якщо відвернути гайку 10 та вийняти клини 11, то закріплений кінець стрижня 2 зможе вільно повертатись на опорі 12, чим забезпечується його шарнірне опирання. Вставивши клин 11 і завернувши гайку 10, можна затиснути нижній кінець стрижня, що відповідає його жорсткому защемленню. Аналогічно змінюється вид закріплення верхнього кінця стрижня 2 у затискному пристрої 3. Отже, установка дозволяє здійснити три способи закріплення кінців стрижня та розглянути чотири типи стиснутих стрижнів (рис. 2.18), що дає змогу оцінити вплив способу закріплення кінців на значення критичної сили. Експериментально критична сила визначається як сила, за якою починається значне викривлення осі початково прямого стрижня. Щоб визначити початок цього явища, використовується індикатор 7, який показує величину прогину середини стрижня.
Рис. 2.19. Схема експериментальної установки дослідження критичної сили стискування стрижня (а) та конструкція затисного пристрою (б) За реальних умов вісь стрижня завжди трохи викривлена, тому згинання стрижня спостерігається і за навантаження меншого за критичне. Прогин середини стрижня у цьому разі визначається за формулою Перрі:
де f – прогин, викликаний силою P; Згідно з цією формулою критичну силу
Пряма по точках проводиться так, щоб розкид був мінімальним. Початковий прогин
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 .
.
 , (2.37)
, (2.37) - мінімальний момент інерції поперечного перерізу стрижня;
- мінімальний момент інерції поперечного перерізу стрижня;  - коефіцієнт приведення довжини, який залежить від способу закріплення кінців стрижня (рис. 2.18); l – довжина стрижня.
- коефіцієнт приведення довжини, який залежить від способу закріплення кінців стрижня (рис. 2.18); l – довжина стрижня.
 , (2.38)
, (2.38) - мінімальний радіус інерції перерізу стрижня,
- мінімальний радіус інерції перерізу стрижня,  ; F – площа поперечного перерізу стрижня; λ – гнучкість стрижня,
; F – площа поперечного перерізу стрижня; λ – гнучкість стрижня,  .
.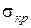 не перевищує границі пропорційності
не перевищує границі пропорційності  , тобто
, тобто . (2.39)
. (2.39) . (2.40)
. (2.40)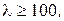 для чавуну -
для чавуну -  , для сосни -
, для сосни -  .
.
 , (2.41)
, (2.41) - початковий прогин стрижня.
- початковий прогин стрижня. (відкладається по осі абсцис); дійсний прогин f (відкладається по осі ординат):
(відкладається по осі абсцис); дійсний прогин f (відкладається по осі ординат): . (2.42)
. (2.42)


