Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уфтхлфхтб й чпънпцопуфй нпдемйтхаэйи рблефпчСодержание книги
Поиск на нашем сайте
Пвэбс фептйс уйуфен нЕФПДЙЮЕУЛЙЕ ХЛБЪБОЙС РП ЧЩРПМОЕОЙА МБВПТБФПТОЩИ ТБВПФ № 1 ‑ 10
уБОЛФ-рЕФЕТВХТЗ уПУФБЧЙФЕМЙ: е. б. дЕМБЛПЧБ,љ б. з. уФЕРБОПЧ, у. р. уПЛПМПЧБ, п. й. ыЙТСЕЧБ тЕГЕОЪЕОФ: РТПЖЕУУПТ нЕЦДХОБТПДОПЗП ВБОЛПЧУЛПЗП ЙОУФЙФХФБ ДПЛФПТ ФЕИОЙЮЕУЛЙИ ОБХЛ н. м. лТЙЮЕЧУЛЙК
љљљљљљљљљљљ нЕФПДЙЮЕУЛЙЕ ХЛБЪБОЙС УПДЕТЦБФ МБВПТБФПТОЩЕ ТБВПФЩ, ГЕМША ЧЩРПМОЕОЙС ЛПФПТЩИ СЧМСЕФУС ЖПТНЙТПЧБОЙЕ ВБЪПЧПК ПУОПЧЩ РПДЗПФПЧЛЙ УРЕГЙБМЙУФПЧ Ч ПВМБУФЙ ЙУРПМШЪПЧБОЙС УПЧТЕНЕООЩИ ФЕИОПМПЗЙК РТЙ ТЕЫЕОЙЙ ЪБДБЮ ЙУУМЕДПЧБОЙС ДЙОБНЙЮЕУЛЙИ УЧПКУФЧ, ПГЕОЙЧБОЙС ЛБЮЕУФЧБ ЪБНЛОХФЩИ УЙУФЕН НЕОЕДЦНЕОФБ У ЙУРПМШЪПЧБОЙЕН ЙОУФТХНЕОФБТЙС ХОЙЧЕТУБМШОПК НБФЕНБФЙЮЕУЛПК УЙУФЕНЩ MATLAB. љљљљљљљљ рТЕДОБЪОБЮЕОЩ ДМС УФХДЕОФПЧ ПЮОПК Й ЪБПЮОПК ЖПТН ПВХЮЕОЙС, ЙЪХЮБАЭЙИ ДЙУГЙРМЙОХ «пВЭБС ФЕПТЙС УЙУФЕН». љљљљљљљљ рПДЗПФПЧМЕОЩ ЛБЖЕДТПК ВЙЪОЕУ-ЙОЖПТНБФЙЛЙ Й ТЕЛПНЕОДПЧБОЩ Л ЙЪДБОЙА ТЕДБЛГЙПООП-ЙЪДБФЕМШУЛЙН УПЧЕФПН уБОЛФ-рЕФЕТВХТЗУЛПЗП ЗПУХДБТУФЧЕООПЗП ХОЙЧЕТУЙФЕФБ БЬТПЛПУНЙЮЕУЛПЗП РТЙВПТПУФТПЕОЙС.
УПДЕТЦБОЙЕ
мбвптбфптобс тбвпфб № 1. тбвпфб ч уйуфене MATLAB.. 4 мбвптбфптобс тбвпфб № 2. ртедуфбчмеойе нбфенбфйюеулйи нпдемек ч ртпуфтбоуфче упуфпсойк й «чипд-чщипд».. 8 мбвптбфптобс тбвпфб № 3. йуумедпчбойе чтенеоощи ибтблфетйуфйл й дйобнйюеулйи учпкуфч фйрпчщи ъчеошеч уйуфен... 16 мбвптбфптобс тбвпфб № 4. ьлчйчбмеофоще ртепвтбъпчбойс уфтхлфхтощи уиен... 16 мбвптбфптобс тбвпфб № 5. лтйфетйй хуфпкюйчпуфй тбъпнлохфщи й ъбнлохфщи уйуфен... 16 мбвптбфптобс тбвпфб № 6. рпуфтпеойе лпттелфйтхаэйи хуфтпкуфч дмс ъбнлохфщи уйуфен... 16 мбвптбфптобс тбвпфб №7. йУУМЕДПЧБОЙЕ ХУФПКЮЙЧПУФЙ тбъпнлохфщи й ъбнлохфщи уйуфенљљ 4 мбвптбфптобс тбвпфб №8. ЛТЙФЕТЙЙ ХУФПКЮЙЧПУФЙ уйуфен.. 9 мбвптбфптобс тбвпфб №9. йуумедпчбойе лбюеуфчеоощи рплбъбфемек бчфпнбфйюеулйи уйуфен.. 17 мбвптбфптобс тбвпфб №10. лпттелгйс уйуфен бчфпнбфйюеулпзп хртбчмеойс.. 23
урйупл мйфетбфхтщ.... 29 мБВПТБФПТОБС ТБВПФБ № 1. тбвпфб ч уйуфене MATLAB
гЕМШ ТБВПФЩ: ПУЧПЕОЙЕ РТПГЕДХТЩ ЖХОЛГЙПОЙТПЧБОЙС ЧЩЮЙУМЙФЕМШОПК УТЕДЩ MATLAB ДМС ТЕБМЙЪБГЙЙ РТПГЕДХТ НБФТЙЮОПЗП БОБМЙЪБ.
хОЙЧЕТУБМШОБС НБФЕНБФЙЮЕУЛБС УЙУФЕНБ (хну) MATLAB СЧМСЕФУС НПЭОЩН УТЕДУФЧПН ТЕЫЕОЙС ОБХЮОП-ФЕИОЙЮЕУЛЙИ, ЙОЦЕОЕТОЩИ Й ЬЛПОПНЙЮЕУЛЙИ ЪБДБЮ. йОУФТХНЕОФБТЙК хну MATLAB РПЪЧПМСЕФ РТПЙЪЧПДЙФШ [1, 2]:
1. нБФЕНБФЙЮЕУЛЙЕ ЧЩЮЙУМЕОЙС. 2. уПЪДБОЙЕ Й ЙУУМЕДПЧБОЙЕ УЧПКУФЧ БМЗПТЙФНПЧ. 3. бОБМЙЪ Й ЙУУМЕДПЧБОЙЕ ЙУИПДОЩИ ДБООЩИ. 4. нПДЕМЙТПЧБОЙЕ ДЙОБНЙЮЕУЛЙИ РТПГЕУУПЧ. 5. тБЪТБВПФЛХ РТЙМПЦЕОЙК, ЧЛМАЮБС УПЪДБОЙЕ ЗТБЖЙЮЕУЛПЗП ЙОФЕТЖЕКУБ.
уФТХЛФХТБ ХОЙЧЕТУБМШОПК НБФЕНБФЙЮЕУЛПК УЙУФЕНЩ MATLAB РТЕДУФБЧМЕОБ ОБ ТЙУ. 1.1.
уТЕДБ MATLAB УПУФПЙФ ЙЪ 4 ПУОПЧОЩИ ПЛПО: ћ Command Window ‑ ЧЩРПМОСАФУС ЛПНБОДЩ РПМШЪПЧБФЕМС, РПДМЕЦБЭЙЕ ОЕНЕДМЕООПНХ ЙУРПМОЕОЙА, Б ФБЛЦЕ ПФПВТБЦБАФУС ТЕЪХМШФБФЩ ЙУРПМОСЕНЩИ ЛПНБОД. чЩЪЧБФШ УРТБЧЛХ ЙЪ ЛПНБОДОПЗП ПЛОБ НПЦОП РТЙ РПНПЭЙ УМЕДХАЭЙИ ЛПНБОД: doc (ПФПВТБЦБЕФ РПДУЛБЪЛХ Ч html-ЖПТНБФЕ), help (ПФПВТБЦБЕФ ФЕЛУФ УРТБЧЛЙ Ч ЛПНБОДОПН ПЛОЕ), lookfor (ПУХЭЕУФЧМСЕФ РПЙУЛ ЛМАЮЕЧПЗП УМПЧБ ЧП ЧУЕИ m-ЖБКМБИ). ћ Command History — ЙУФПТЙС ЛПНБОД. иТБОСФУС ЧУЕ ЛПНБОДЩ, ОБВЙТБЕНЩЕ РПМШЪПЧБФЕМЕН, ОЕ РПРБДБАФ УППВЭЕОЙС УЙУФЕНЩ Й ТЕЪХМШФБФЩ ЧЩЮЙУМЕОЙК. ћ Workspace — ТБВПЮЕЕ РТПУФТБОУФЧП. рТЕДУФБЧМСЕФ УПВПК ФЕЛХЭЙК ОБВПТ РЕТЕНЕООЩИ (ЙНС, ТБЪНЕТ, ФЙР). ћ Current Directory — ФЕЛХЭБС ДЙТЕЛФПТЙС.
ЪБДБОЙЕ НБФТЙГ рП ХНПМЮБОЙА ЧУЕ ЮЙУМПЧЩЕ РЕТЕНЕООЩЕ Ч MATLAB УЮЙФБАФУС НБФТЙГБНЙ У ЛПНРМЕЛУОЩНЙ ЮЙУМБНЙ. уЛБМСТОБС ЧЕМЙЮЙОБ ЕУФШ НБФТЙГБ РЕТЧПЗП РПТСДЛБ, Б ЧЕЛФПТЩ СЧМСАФУС НБФТЙГБНЙ, УПУФПСЭЙНЙ ЙЪ ПДОПЗП УФПМВГБ. нБФТЙГХ НПЦОП ЧЧЕУФЙ, ЪБДБЧБС ЬМЕНЕОФЩ НБФТЙГЩ ЙМЙ УЮЙФЩЧБС ДБООЩЕ ЙЪ ЖБКМБ, Б ФБЛЦЕ Ч ТЕЪХМШФБФЕ ПВТБЭЕОЙС Л УФБОДБТФОПК ЙМЙ ОБРЙУБООПК РПМШЪПЧБФЕМЕН ЖХОЛГЙЙ. ьМЕНЕОФЩ НБФТЙГЩ Ч РТЕДЕМБИ УФТПЛЙ ПФДЕМСАФУС РТПВЕМБНЙ ЙМЙ ЪБРСФЩНЙ. [ ] – ЛЧБДТБФОЩЕ УЛПВЛЙ ЙУРПМШЪХАФУС РТЙ ЪБДБОЙЙ НБФТЙГ Й ЧЕЛФПТПЧ; РТПВЕМ УМХЦЙФ ДМС ТБЪДЕМЕОЙС ЬМЕНЕОФПЧ НБФТЙГ; ,љљљљ ЪБРСФБС РТЙНЕОСЕФУС ДМС ТБЪДЕМЕОЙС ЬМЕНЕОФПЧ НБФТЙГ Й ПРЕТБФПТПЧ Ч УФТПЛЕ ЧЧПДБ; ;љљљљ ФПЮЛБ У ЪБРСФПК ПФДЕМСЕФ УФТПЛЙ НБФТЙГ, Б ФПЮЛБ У ЪБРСФПК Ч ЛПОГЕ ПРЕТБФПТБ (ЛПНБОДЩ) ПФНЕОСЕФ ЧЩЧПД ТЕЪХМШФБФБ ОБ ЬЛТБО; :љљљљ ДЧПЕФПЮЙЕ ЙУРПМШЪХЕФУС ДМС ХЛБЪБОЙС ДЙБРБЪПОБ (ЙОФЕТЧБМБ ЙЪНЕОЕОЙС ЧЕМЙЮЙОЩ) Й Ч ЛБЮЕУФЧЕ ЪОБЛБ ЗТХРРПЧПК ПРЕТБГЙЙ ОБД ЬМЕНЕОФБНЙ НБФТЙГ; ()љљ ЛТХЗМЩЕ УЛПВЛЙ РТЙНЕОСАФУС ДМС ЪБДБОЙС РПТСДЛБ ЧЩРПМОЕОЙС НБФЕНБФЙЮЕУЛЙИ ПРЕТБГЙК, Б ФБЛЦЕ ДМС ХЛБЪБОЙС БТЗХНЕОФПЧ ЖХОЛГЙК Й ЙОДЕЛУПЧ НБФТЙГ;
.љљљљ ФПЮЛБ ПФДЕМСЕФ ДТПВОХА ЮБУФШ ЮЙУМБ ПФ ГЕМПК ЕЗП ЮБУФЙ, Б ФБЛЦЕ РТЙНЕОСЕФУС Ч УПУФБЧЕ ЛПНВЙОЙТПЧБООЩИ ЪОБЛПЧ; …љ ФТЙ ФПЮЛЙ Й ВПМЕЕ Ч ЛПОГЕ УФТПЛЙ ПФНЕЮБАФ РТПДПМЦЕОЙЕ ЧЩТБЦЕОЙС ОБ УМЕДХАЭЕК УФТПЛЕ; %љ ЪОБЛ РТПГЕОФБ ПВПЪОБЮБЕФ ОБЮБМП ЛПННЕОФБТЙС.
НБФТЙЮОЩЕ ЧЩЮЙУМЕОЙС ЖХОЛГЙЙ ПРЙУБОЙС НБФТЙГ eyeљљљљљљљ ЕДЙОЙЮОБС НБФТЙГБ; zerosљљљљ ОХМЕЧБС НБФТЙГБ; onesљљљљљ НБФТЙГБ ЙЪ ЕДЙОЙГ; randљљљљљ УМХЮБКОБС НБФТЙГБ УП ЪОБЮЕОЙСНЙ ЙЪ ЙОФЕТЧБМБ [0,1]; diagљљљљљљ УПЪДБОЙЕ ДЙБЗПОБМШОПК НБФТЙГЩ ЙМЙ ЧЩДЕМЕОЙЕ ДЙБЗПОБМЙ.
ЪОБЛЙ ПРЕТБГЙК +,-љљљљљљљљ УЙНЧПМЩ РМАУ Й НЙОХУ ПВПЪОБЮБАФ ЪОБЛ ЮЙУМБ ЙМЙ ПРЕТБГЙА УМПЦЕОЙС ЙМЙ ЧЩЮЙФБОЙС НБФТЙГ, РТЙЮЕН НБФТЙГЩ ДПМЦОЩ ВЩФШ ПДОПК ТБЪНЕТОПУФЙ; *љљљљљљљљљљ ЪОБЛ ХНОПЦЕОЙС ПВПЪОБЮБЕФ НБФТЙЮОПЕ ХНОПЦЕОЙЕ; ‘љљљљљљљљљљљ БРПУФТПЖ ПВПЪОБЮБЕФ ПРЕТБГЙА ФТБОУРПОЙТПЧБОЙС (ЧНЕУФЕ У ЛПНРМЕЛУОЩН УПРТСЦЕОЙЕН); /љљљљљљљљљљљљ МЕЧПЕ ДЕМЕОЙЕ; \љљљљљљљљљљљљ РТБЧПЕ ДЕМЕОЙЕ; ^љљљљљљљљљљљ ПРЕТБФПТ ЧПЪЧЕДЕОЙС Ч УФЕРЕОШ.
НБФТЙЮОЩЕ ИБТБЛФЕТЙУФЙЛЙ
detљљљљљљљљ ЧЩЮЙУМЕОЙЕ ПРТЕДЕМЙФЕМС; traceљљљљљ ЧЩЮЙУМЕОЙЕ УМЕДБ НБФТЙГЩ; rankљљљљљ ПРТЕДЕМЕОЙЕ ТБОЗБ НБФТЙГЩ; normљљљљ ЧЩЮЙУМЕОЙЕ ОПТНЩ НБФТЙГЩ.
ЛПНБОДЩ МЙОЕКОПК БМЗЕВТЩ invљљљљљљљљ ЧЩЮЙУМЕОЙЕ ПВТБФОПК НБФТЙГЩ; pinvљљљљљ ЧЩЮЙУМЕОЙЕ РУЕЧДППВТБФОПК НБФТЙГЩ; nullљљљљљљљ ПРТЕДЕМЕОЙЕ СДТБ (ОХМШ-РТПУФТБОУФЧБ) НБФТЙГЩ; orthљљљљљљ ЧЩЮЙУМЕОЙЕ ПТФПОПТНЙТПЧБООПЗП ВБЪЙУБ. ЛПНБОДЩ ЧЩЮЙУМЕОЙС УРЕЛФТБ
polyљљљљљ ЧЩЮЙУМЕОЙЕ ИБТБЛФЕТЙУФЙЮЕУЛПЗП РПМЙОПНБ ДМС ЛЧБДТБФОПК НБФТЙГЩ. ч ТЕЪХМШФБФЕ ЧЩРПМОЕОЙС ЛПНБОДЩ ВХДХФ РПМХЮЕОЩ ЛПЬЖЖЙГЙЕОФЩ ОПТНЙТПЧБООПЗП ИБТБЛФЕТЙУФЙЮЕУЛПЗП РПМЙОПНБ a1, a2, ….,an: det(pE – A)=pn +a1pn-1 +a2pn-2 + ….+ an; polyeigљ ЧЩЮЙУМЕОЙЕ УПВУФЧЕООЩИ ЪОБЮЕОЙК НБФТЙЮОПЗП РПМЙОПНБ; eigљљљљљљљљ ЧЩЮЙУМЕОЙЕ УПВУФЧЕООЩИ ЮЙУЕМ Й ЧЕЛФПТПЧ.
дМС ПРТЕДЕМЕОЙС УПВУФЧЕООЩИ ЪОБЮЕОЙК Й УПВУФЧЕООЩИ ЧЕЛФПТПЧ НБФТЙГЩ б УМХЦЙФ ЛПНБОДБ
[U, D] = eig(A).
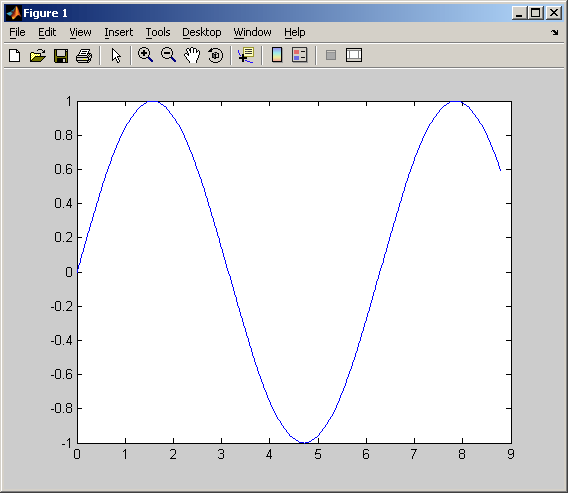
ъДЕУШ ДЙБЗПОБМШОБС НБФТЙГБ D УПУФПЙФ ЙЪ УПВУФЧЕООЩИ ЮЙУЕМ, Б НБФТЙГБ U УПУФБЧМЕОБ ЙЪ УПВУФЧЕООЩИ ЧЕЛФПТПЧ-УФПМВГПЧ НБФТЙГЩ б. еУМЙ Ч МЕЧПК ЮБУФЙ ХЛБЪБО ЕДЙОУФЧЕООЩК ЧЩИПДОПК РБТБНЕФТ, ФП ТЕЪХМШФБФПН ВХДЕФ ЧЩУФХРБФШ ЧЕЛФПТ-УФПМВЕГ УПВУФЧЕООЩИ ЮЙУЕМ eig(A). УПЪДБОЙЕ ЗТБЖЙЛБ MATLAB ЙНЕЕФ ЫЙТПЛЙЕ ЧПЪНПЦОПУФЙ ДМС ЗТБЖЙЮЕУЛПЗП ЙЪПВТБЦЕОЙС ЧЕЛФПТПЧ Й НБФТЙГ, Б ФБЛЦЕ ДМС УПЪДБОЙС ЛПННЕОФБТЙЕЧ Й РЕЮБФЙ ЗТБЖЙЛПЧ. рТЙЧЕДЕН ПРЙУБОЙЕ ОЕУЛПМШЛП ЧБЦОЩИ ЗТБЖЙЮЕУЛЙИ ЖХОЛГЙК. жХОЛГЙС plot ЙНЕЕФ ТБЪМЙЮОЩЕ ЖПТНЩ, УЧСЪБООЩЕ У ЧИПДОЩНЙ РБТБНЕФТБНЙ, ОБРТЙНЕТ plot(y) УПЪДБЕФ ЛХУПЮОП-МЙОЕКОЩК ЗТБЖЙЛ ЪБЧЙУЙНПУФЙ ЬМЕНЕОФПЧ y ПФ ЙИ ЙОДЕЛУПЧ. еУМЙ Ч ЛБЮЕУФЧЕ БТЗХНЕОФПЧ ЪБДБОЩ ДЧБ ЧЕЛФПТБ, ФП plot(x,y) УПЪДБУФ ЗТБЖЙЛ ЪБЧЙУЙНПУФЙ y ПФ x. љ тЙУХОПЛ 1.2. рТЙНЕТ ЛПНБОД ДМС РПУФТПЕОЙС ЗТБЖЙЛБ ЖХОЛГЙЙ sin Ч ЙОФЕТЧБМЕ ПФ 0 ДП 2p рТПЗТБННБ РПУФТПЙМБ ЗТБЖЙЛ ЪБЧЙУЙНПУФЙ, ЛПФПТЩК ПФПВТБЦБЕФУС Ч ПЛОЕ тЙУХОПЛ 1.3.
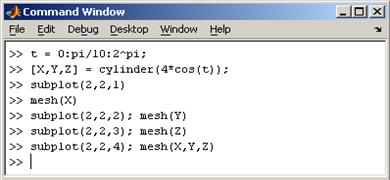
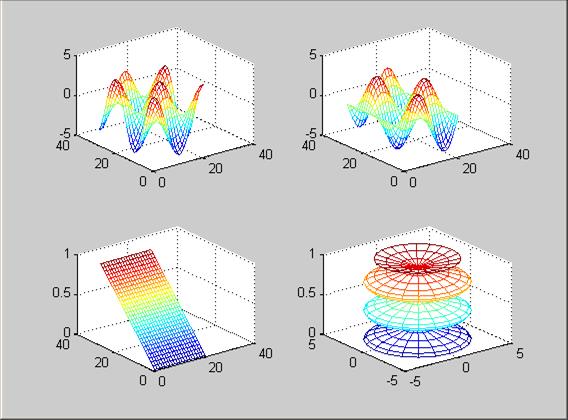
тЙУХОПЛ 1.3. зТБЖЙЛ ЖХОЛГЙЙ sin Ч ЙОФЕТЧБМЕ ПФ 0 ДП 2p MATLAB БЧФПНБФЙЮЕУЛЙ РТЙУЧБЙЧБЕФ ЛБЦДПНХ ЗТБЖЙЛХ УЧПК ГЧЕФ (ЙУЛМАЮБС УМХЮБЙ, ЛПЗДБ ЬФП ДЕМБЕФ РПМШЪПЧБФЕМШ), ЮФП РПЪЧПМСЕФ ТБЪМЙЮБФШ ОБВПТЩ ДБООЩИ. лПНБОДБ hold on РПЪЧПМСЕФ ДПВБЧМСФШ ЛТЙЧЩЕ ОБ УХЭЕУФЧХАЭЙК ЗТБЖЙЛ. жХОЛГЙС subplot РПЪЧПМСЕФ ЧЩЧПДЙФШ НОПЦЕУФЧП ЗТБЖЙЛПЧ Ч ПДОПН ПЛОЕ
тЙУХОПЛ 1.4. рТЙНЕТ ЙУРПМШЪПЧБОЙС ЖХОЛГЙЙ subplot.
тЙУХОПЛ 1.15. тЕЪХМШФБФ ЙУРПМШЪПЧБОЙС ЖХОЛГЙЙ subplot.
РЕЮБФШ ЗТБЖЙЛПЧ рХОЛФ Print Ч НЕОА File Й ЛПНБОДБ print РЕЮБФБАФ ЗТБЖЙЛХ MATLAB. нЕОА Print ЧЩЪЩЧБЕФ ДЙБМПЗПЧПЕ ПЛОП, ЛПФПТПЕ РПЪЧПМСЕФ ЧЩВЙТБФШ ПВЭЙЕ УФБОДБТФОЩЕ ЧБТЙБОФЩ РЕЮБФЙ. лПНБОДБ print ПВЕУРЕЮЙЧБЕФ ВПМШЫХА ЗЙВЛПУФШ РТЙ ЧЩЧПДЕ ЧЩИПДОЩИ ДБООЩИ Й РПЪЧПМСЕФ ЛПОФТПМЙТПЧБФШ РЕЮБФШ ЙЪ н-ЖБКМПЧ. тЕЪХМШФБФ НПЦЕФ ВЩФШ РПУМБО РТСНП ОБ РТЙОФЕТ, ЧЩВТБООЩК РП ХНПМЮБОЙА, ЙМЙ УПИТБОЕО Ч ЪБДБООПН ЖБКМЕ.
1.3. мБВПТБФПТОБС ТБВПФБ № 1 гЕМШ ТБВПФЩ: ПУЧПЙФШ ПРЕТБГЙЙ НБФТЙЮОЩИ ЧЩЮЙУМЕОЙК УТЕДУФЧБНЙ ХОЙЧЕТУБМШОПК УЙУФЕНЩ MATLAB.
ВБЪПЧЩЕ УЧЕДЕОЙС нБФТЙГЕК ОБЪЩЧБЕФУС РТСНПХЗПМШОБС ФБВМЙГБ ЮЙУЕМ, ЛПФПТБС ПВПЪОБЮБЕФУС ЪБЗМБЧОПК РПМХЦЙТОПК ВХЛЧПК, Л РТЙНЕТХ ( A ), Б ЕЕ ЬМЕНЕОФЩ — УППФЧЕФУФЧХАЭЙНЙ УФТПЮОЩНЙ ВХЛЧБНЙ У ЙОДЕЛУБНЙ, Ф.Е. aij. рЕТЧЩК ЙОДЕЛУ ОХНЕТХЕФ УФТПЛЙ, Б ЧФПТПК — УФПМВГЩ. нБФТЙГЩ НПЦОП ХНОПЦБФШ ОБ ЮЙУМБ. рТЙ ЬФПН ЛБЦДЩК ЬМЕНЕОФ ХНОПЦБЕФУС ОБ ЬФП ЮЙУМП. дЧЕ НБФТЙГЩ ПДЙОБЛПЧПК ТБЪНЕТОПУФЙ НПЦОП РПЬМЕНЕОФОП УЛМБДЩЧБФШ Й ЧЩЮЙФБФШ. ч ТЕЪХМШФБФЕ ХНОПЦЕОЙС ОБ ЮЙУМП Й УМПЦЕОЙС РПМХЮБЕФУС НБФТЙГБ ФПК ЦЕ ТБЪНЕТОПУФЙ. оХМЕЧПК НБФТЙГЕК ОБЪЩЧБЕФУС НБФТЙГБ, УПУФПСЭБС ЙЪ ОХМЕК. пОБ ПВПЪОБЮБЕФУС O. пЮЕЧЙДОП, ЮФП A + O = A, A − A = O Й 0 A = O. нБФТЙГХ НПЦОП ФТБОУРПОЙТПЧБФШ. рТЙ ЬФПК ПРЕТБГЙЙ НБФТЙГБ РЕТЕЧПТБЮЙЧБЕФУС, Ф.Е. УФТПЛЙ Й УФПМВГЩ НЕОСАФУС НЕУФБНЙ. фТБОУРПОЙТПЧБОЙЕ ПВПЪОБЮБЕФУС ЫФТЙИПН, A ' ЙМЙ ЙОДЕЛУПН A ф. фБЛЙН ПВТБЪПН, ЕУМЙ A = {aij, i =,..., m; j = 1,...,n}, ФП A T = {aji, j = 1,...,n; i = 1,..., m}. пЮЕЧЙДОП, ЮФП (A T)T = A, (A + B)T = A T+ B T. нБФТЙГЩ НПЦОП РЕТЕНОПЦБФШ, ОП ФПМШЛП Ч ФПН УМХЮБЕ, ЛПЗДБ ПОЙ ЙНЕАФ УППФЧЕФУФЧХАЭЙЕ ТБЪНЕТОПУФЙ. рТПЙЪЧЕДЕОЙЕН НБФТЙГЩ A, ТБЪНЕТОПУФША m × l, Й НБФТЙГЩ B, ТБЪНЕТОПУФША l × n, ОБЪЩЧБЕФУС НБФТЙГБ C, ТБЪНЕТОПУФША m × n. рТБЧЙМП УЛБМСТОПЗП РЕТЕНОПЦЕОЙС НБФТЙГ НПЦОП УЖПТНХМЙТПЧБФШ ФБЛ. дМС ФПЗП, ЮФПВЩ ОБКФЙ ЬМЕНЕОФ НБФТЙГЩ C, УФПСЭЙК ОБ РЕТЕУЕЮЕОЙЙ i -ПК УФТПЛЙ Й j -ПЗП УФПМВГБ (cij) ОБДП РПЬМЕНЕОФОП РЕТЕНОПЦЙФШ i - ХА УФТПЛХ РЕТЧПК НБФТЙГЩ A ОБ j - ЩК УФПМВЕГ ЧФПТПК НБФТЙГЩ B Й УМПЦЙФШ ЧУЕ ТЕЪХМШФБФЩ. рТПЙЪЧЕДЕОЙЕ НБФТЙГ ЪБЧЙУЙФ ПФ РПТСДЛБ ЙИ ХНОПЦЕОЙС, Ф.Е. AB ≠ BA, ИПФС ВЩ РП УППВТБЦЕОЙСН ТБЪНЕТОПУФЙ. зПЧПТСФ, ЮФП ПОП ОЕЛПННХФБФЙЧОП. пДОБЛП РТПЙЪЧЕДЕОЙЕ НБФТЙГ БУУПГЙБФЙЧОП. ьФП ПЪОБЮБЕФ, ЮФП ABC = ( AB ) C = A ( BC ). лТПНЕ ФПЗП, ПОП ЕЭЕ Й ДЙУФТЙВХФЙЧОП, Ф.Е. A ( B + C ) = AB + AC. пЮЕЧЙДОП, ЮФП AO = O. еУМЙ ЮЙУМП УФПМВГПЧ НБФТЙГЩ ТБЧОП ЮЙУМХ ЕЕ УФТПЛ (m = n =k), ФП ФБЛБС НБФТЙГБ ОБЪЩЧБЕФУС ЛЧБДТБФОПК. уТЕДЙ ЬФЙИ НБФТЙГ НПЦОП ЧЩДЕМЙФШ НБФТЙГЩ, ПВМБДБАЭЙЕ ПУПВЩНЙ УЧПКУФЧБНЙ. еДЙОЙЮОПК НБФТЙГЕК (ПВПЪОБЮБЕФУС I, Б ЙОПЗДБ E) ОБЪЩЧБЕФУС НБФТЙГБ, Х ЛПФПТПК ЧУЕ ЬМЕНЕОФЩ ТБЧОЩ ОХМА, ЪБ ЙУЛМАЮЕОЙЕН ДЙБЗПОБМШОЩИ, ЛПФПТЩЕ ТБЧОЩ 1. пЮЕЧЙДОП AI = IA = A. нБФТЙГБ ОБЪЩЧБЕФУС ДЙБЗПОБМШОПК, ЕУМЙ ЧУЕ ЕЕ ЬМЕНЕОФЩ, ЛТПНЕ ДЙБЗПОБМШОЩИ (aii) ТБЧОЩ ОХМА. нБФТЙГБ A ОБЪЩЧБЕФУС ЧЕТИОЕК ФТЕХЗПМШОПК, ЕУМЙ ЧУЕ ЕЕ ЬМЕНЕОФЩ, МЕЦБЭЙЕ ОЙЦЕ ДЙБЗПОБМЙ, ТБЧОЩ ОХМА, Ф.Е. aij = 0, РТЙ i > j. бОБМПЗЙЮОП ПРТЕДЕМСЕФУС Й ОЙЦОСС ФТЕХЗПМШОБС НБФТЙГБ. нБФТЙГБ A ОБЪЩЧБЕФУС УЙННЕФТЙЮОПК, ЕУМЙ A T = A. йОЩНЙ УМПЧБНЙ aij = aji. нБФТЙГБ A ОБЪЩЧБЕФУС ПТФПЗПОБМШОПК, ЕУМЙ A T A = AA T = I. нБФТЙГБ ОБЪЩЧБЕФУС ОПТНБМШОПК ЕУМЙ A T A = AA T.
уМЕДПН ЛЧБДТБФОПК НБФТЙГЩ A (ПВПЪОБЮБЕФУС Tr( A ) ЙМЙ Sp( A )) ОБЪЩЧБЕФУС УХННБ ЕЕ ДЙБЗПОБМШОЩИ ЬМЕНЕОФПЧ,
пЮЕЧЙДОП, ЮФП Sp(α A ) = α Sp( A ) Й Sp(A + B) = Sp(A)+ Sp(B). нПЦОП РПЛБЪБФШ, ЮФП Sp(A) = Sp(A T), Sp(I) = N, Б ФБЛЦЕ, ЮФП Sp( AB ) = Sp( BA ). дТХЗПК ЧБЦОПК ИБТБЛФЕТЙУФЙЛПК ЛЧБДТБФОПК НБФТЙГЩ СЧМСЕФУС ЕЕ ПРТЕДЕМЙФЕМШ (ПВПЪОБЮБЕФУС det(A)). пРТЕДЕМЕОЙЕ ПРТЕДЕМЙФЕМС Ч ПВЭЕН УМХЮБЕ ДПЧПМШОП УМПЦОП, РПЬФПНХ НЩ ОБЮОЕН У РТПУФЕКЫЕЗП ЧБТЙБОФБ — НБФТЙГЩ A ТБЪНЕТОПУФША (2×2). фПЗДБ
дМС НБФТЙГЩ (3×3) ПРТЕДЕМЙФЕМШ ВХДЕФ ТБЧЕО
уРТБЧЕДМЙЧЩ УМЕДХАЭЙЕ УЧПКУФЧБ: det( I ) = 1, det( A ) = det( A ф), det(AB) = det(A)det(B). лЧБДТБФОБС НБФТЙГБ A ОБЪЩЧБЕФУС ОЕЧЩТПЦДЕООПК, ЕУМЙ ПОБ ЙНЕЕФ ЕДЙОУФЧЕООХА ПВТБФОХА НБФТЙГХ A -1, ПРТЕДЕМСЕНХА ХУМПЧЙСНЙ AA −1 = A −1 A = I. пВТБФОБС НБФТЙГБ УХЭЕУФЧХЕФ ОЕ ДМС ЧУЕИ НБФТЙГ. оЕПВИПДЙНЩН Й ДПУФБФПЮОЩН ХУМПЧЙЕН ОЕЧЩТПЦДЕООПУФЙ СЧМСЕФУС det(A) ≠ 0 ЙМЙ rank(A) = N. еУМЙ НБФТЙГЩ A Й B ОЕЧЩТПЦДЕОЩ, ФП ( AB )−1 = B −1 A −1. еУМЙ НБФТЙГБ A ЧЩТПЦДЕОБ Й ПВТБФОБС НБФТЙГБ ОЕ УХЭЕУФЧХЕФ, ФП Ч ОЕЛПФПТЩИ УМХЮБСИ НПЦОП ЙУРПМШЪПЧБФШ РУЕЧДППВТБФОХА НБФТЙГХ, ЛПФПТБС ПРТЕДЕМСЕФУС ЛБЛ ФБЛБС НБФТЙГБ A +, ЮФП AA + A = A. рУЕЧДПВТБФОБС НБФТЙГБ — ОЕ ЕДЙОУФЧЕООБС Й ЕЕ ЧЙД ЪБЧЙУЙФ ПФ УРПУПВБ РПУФТПЕОЙС. л РТЙНЕТХ, ЕУМЙ НБФТЙГБ б СЧМСЕФУС РТСНПХЗПМШОПК, ФП НПЦОП ЧПУРПМШЪПЧБФШУС ХУМПЧЙСНЙ нХТБ-рЕОТПХЪБ: ЕУМЙ ЮЙУМП УФПМВГПЧ НЕОШЫЕ ЮЙУМБ УФТПЛ, ФП РУЕЧДППВТБФОБС НБФТЙГБ A + РТЕДУФБЧМСЕФУС, ЛБЛ A +=( A ф A )−1 A ф. еУМЙ НБФТЙГБ УПУФПЙФ ФПМШЛП ЙЪ ПДОПЗП УФПМВГБ (n = 1), ФП ФБЛПК ПВЯЕЛФ ОБЪЩЧБЕФУС ЧЕЛФПТПН. фПЮОЕЕ ЗПЧПТС, ЧЕЛФПТПН-УФПМВГПН. нПЦОП ТБУУНБФТЙЧБФШ Й НБФТЙГЩ, УПУФПСЭЙЕ ЙЪ ПДОПК УФТПЛЙ. ьФПФ ПВЯЕЛФ ФБЛЦЕ СЧМСЕФУС ЧЕЛФПТПН, ОП ЧЕЛФПТПН-УФТПЛПК. уЛБМСТОПЕ РТПЙЪЧЕДЕОЙЕ ЧЕЛФПТБ УБНПЗП ОБ УЕВС ОБЪЩЧБЕФУС УЛБМСТОЩН ЛЧБДТБФПН. ьФБ ЧЕМЙЮЙОБ
ПРТЕДЕМСЕФ ЛЧБДТБФ ДМЙОЩ ЧЕЛФПТБ x. дМС ПВПЪОБЮЕОЙС ДМЙОЩ (ОБЪЩЧБЕНПК ФБЛЦЕ ОПТНПК ЧЕЛФПТБ) ЙУРПМШЪХЕФУС ПВПЪОБЮЕОЙЕ
чЕЛФПТ ЕДЙОЙЮОПК ДМЙОЩ (|| x || = 1) ОБЪЩЧБЕФУС ОПТНЙТПЧБООЩН. оЕОХМЕЧПК ЧЕЛФПТ (x ≠ 0) НПЦОП ОПТНЙТПЧБФШ, ТБЪДЕМЙЧ ЕЗП ОБ ДМЙОХ, Ф.Е. x = || x || ( x/ || x ||) = || x || e. ъДЕУШ e = x/ || x || — ОПТНЙТПЧБООЩК ЧЕЛФПТ. чЕЛФПТЩ ОБЪЩЧБАФУС ПТФПОПТНЙТПЧБООЩНЙ, ЕУМЙ ЧУЕ ПОЙ ОПТНЙТПЧБОЩ Й РПРБТОП ПТФПЗПОБМШОЩ. љљљљљљљљ уПВУФЧЕООЩЕ ЪОБЮЕОЙС Й УПВУФЧЕООЩЕ ЧЕЛФПТЩ рХУФШ A — ЬФП ЛЧБДТБФОБС НБФТЙГБ. чЕЛФПТ v ОБЪЩЧБЕФУС УПВУФЧЕООЩН ЧЕЛФПТПН НБФТЙГЩ A, ЕУМЙ Av = λ v, ЗДЕ ЮЙУМП λ ОБЪЩЧБЕФУС УПВУФЧЕООЩН ЪОБЮЕОЙЕН НБФТЙГЩ A. фБЛЙН ПВТБЪПН, РТЕПВТБЪПЧБОЙЕ, ЛПФПТПЕ ЧЩРПМОСЕФ НБФТЙГБ A ОБД ЧЕЛФПТПН v, УЧПДЙФУС Л РТПУФПНХ ТБУФСЦЕОЙА ЙМЙ УЦБФЙА У ЛПЬЖЖЙГЙЕОФПН λ. уПВУФЧЕООЩК ЧЕЛФПТ ПРТЕДЕМСЕФУС У ФПЮОПУФША ДП ХНОПЦЕОЙС ОБ ЛПОУФБОФХ α ≠ 0, Ф.Е. ЕУМЙ v — УПВУФЧЕООЩК ЧЕЛФПТ, ФП Й α v — ФПЦЕ УПВУФЧЕООЩК ЧЕЛФПТ. х НБФТЙГЩ A, ТБЪНЕТОПУФЙ (n × n) ОЕ НПЦЕФ ВЩФШ ВПМШЫЕ ЮЕН n УПВУФЧЕООЩИ ЪОБЮЕОЙК. пОЙ ХДПЧМЕФЧПТСАФ ИБТБЛФЕТЙУФЙЮЕУЛПНХ ХТБЧОЕОЙА det( A − λ I) = 0, СЧМСАЭЕНХУС БМЗЕВТБЙЮЕУЛЙН ХТБЧОЕОЙЕН n -ЗП РПТСДЛБ. ч ЮБУФОПУФЙ, ДМС НБФТЙГЩ 2×2 ИБТБЛФЕТЙУФЙЮЕУЛПЕ ХТБЧОЕОЙЕ ЙНЕЕФ ЧЙД
оБВПТ УПВУФЧЕООЩИ ЪОБЮЕОЙК λ1,..., λn НБФТЙГЩ A ОБЪЩЧБЕФУС УРЕЛФТПН A. уРЕЛФТ ПВМБДБЕФ ТБЪОППВТБЪОЩНЙ УЧПКУФЧБНЙ. ч ЮБУФОПУФЙ det(A) = λ1×...× λn, Sp(A) = λ1+...+ λn. уПВУФЧЕООЩЕ ЪОБЮЕОЙС РТПЙЪЧПМШОПК НБФТЙГЩ НПЗХФ ВЩФШ ЛПНРМЕЛУОЩНЙ ЮЙУМБНЙ, ПДОБЛП ЕУМЙ НБФТЙГБ УЙННЕФТЙЮОБС (A T = A), ФП ЕЕ УПВУФЧЕООЩЕ ЪОБЮЕОЙС ЧЕЭЕУФЧЕООЩ.
РПТСДПЛ ЧЩРПМОЕОЙС ТБВПФЩ уЖПТНЙТПЧБФШ ЙУИПДОЩЕ НБФТЙГЩ: б ТБЪНЕТОПУФЙ (3×3), ч Й у ТБЪНЕТОПУФЙ (3×4) Й ЧЕЛФПТЩ b Й c УППФЧЕФУФЧХАЭЙИ ТБЪНЕТОПУФЕК. чЩЮЙУМЙФШ: -љљ ПРТЕДЕМЙФЕМШ, УМЕД НБФТЙГЩ; -љљ ФТБОУРПОЙТПЧБООЩЕ НБФТЙГЩ, ЙИ УХННХ, ТБЪОПУФШ, РТПЙЪЧЕДЕОЙЕ УЛБМСТОПК ЧЕМЙЮЙОЩ ОБ НБФТЙГХ, УЛБМСТОПЕ РТПЙЪЧЕДЕОЙЕ НБФТЙГ, ЕЧЛМЙДПЧЩ ОПТНЩ, ПВТБФОХА Й РУЕЧДППВТБФОХА НБФТЙГХ; -љљ РТПЙЪЧЕДЕОЙЕ НБФТЙГЩ ОБ ЧЕЛФПТ, УФТПЛЙ ОБ НБФТЙГХ; - ЧЕЛФПТОПЕ РТПЙЪЧЕДЕОЙЕ ЧЕЛФПТБ ОБ УФТПЛХ; -љљљ УПВУФЧЕООЩЕ ЪОБЮЕОЙС Й УПВУФЧЕООЩЕ ЧЕЛФПТЩ УЖПТНЙТПЧБООЩИ НБФТЙГ.
ПЖПТНМЕОЙЕ ПФЮЕФБ рПДЗПФПЧШФЕ ПФЮЕФ П ЧЩРПМОЕООПК МБВПТБФПТОПК ТБВПФЕ. пО ДПМЦЕО УПДЕТЦБФШ ФЙФХМШОЩК МЙУФ, ЖПТНХМЙТПЧЛХ ЪБДБОЙС, ТЕЪХМШФБФЩ НБФТЙЮОЩИ ЧЩЮЙУМЕОЙК. уЖПТНХМЙТХКФЕ ЧЩЧПДЩ, ЛПФПТЩЕ НПЦОП УДЕМБФШ РП ТЕЪХМШФБФБН ЧЩРПМОЕООПК ТБВПФЩ. чБТЙБОФ ФЙФХМШОПЗП МЙУФБ ПФЮЕФБ, НПЦОП ОБКФЙ ОБ http://standarts.guap.ru ч РТПГЕУУЕ УДБЮЙ ПФЮЕФБ УФХДЕОФ ДПМЦЕО ПФЧЕФЙФШ ОБ РТЕДМБЗБЕНЩЕ ЛПОФТПМШОЩЕ ЧПРТПУЩ Й ЧЩРПМОЙФШ ХРТБЦОЕОЙС РП ЙЪХЮБЕНПК ФЕНЕ.
ЛПОФТПМШОЩЕ ЧПРТПУЩ 1. хУМПЧЙЕ ОЕЧЩТПЦДЕООПУФЙ НБФТЙГЩ. 2. юФП ФБЛПЕ УМЕД НБФТЙГЩ? 3. у РПНПЭША ЛБЛЙИ ПРЕТБФПТПЧ ЧЩЮЙУМСАФУС Ч MATLAB ПВТБФОБС Й РУЕЧДППВТБФОБС НБФТЙГЩ? 4. нПЗХФ МЙ УПВУФЧЕООЩЕ ЪОБЮЕОЙС НБФТЙГЩ ЧЩТБЦБФШУС ЛПНРМЕЛУОЩНЙ ЮЙУМБНЙ? 5. чЩРПМОСАФУС МЙ ХУМПЧЙС ЛПННХФБФЙЧОПУФЙ ДМС РТПЙЪЧЕДЕОЙС НБФТЙГ? мБВПТБФПТОБС ТБВПФБ № 2. гЕМШ ТБВПФЩ: РТЙПВТЕФЕОЙЕ ПУОПЧОЩИ ОБЧЩЛПЧ ТБВПФЩ У НПДЕМЙТХАЭЙНЙ РТПЗТБННОЩНЙ РБЛЕФБНЙ MATLAB. ПУОПЧОЩЕ УЧЕДЕОЙС
MATLAB – УЙУФЕНБ РТПЗТБННЙТПЧБОЙС ЧЩУПЛПЗП ХТПЧОС. пОБ НПЦЕФ ЖХОЛГЙПОЙТПЧБФШ ЛБЛ ЙОФЕТРТЕФБФПТ Й ЧЛМАЮБЕФ ВПМШЫПК ОБВПТ ЛПНБОД ДМС ЧЩРПМОЕОЙС ТБЪОППВТБЪОЩИ ЧЩЮЙУМЕОЙК, ЪБДБОЙС УФТХЛФХТ ДБООЩИ Й ЗТБЖЙЮЕУЛПЗП РТЕДУФБЧМЕОЙС ТЕЪХМШФБФПЧ ТБУЮЕФПЧ. дМС НПДЕМЙТПЧБОЙС РТПГЕУУПЧ ЙУРПМШЪХАФУС ЛПНБОДЩ РБЛЕФБ РТЙЛМБДОЩИ РТПЗТБНН Control System Toolbox, РТЕДОБЪОБЮЕООПЗП ДМС ТБВПФЩ У LTI–НПДЕМСНЙ (Linear Time Invariant Models) УЙУФЕН ХРТБЧМЕОЙС. MATLAB Simulink – ЙОФЕТБЛФЙЧОЩК ЙОУФТХНЕОФ ДМС НПДЕМЙТПЧБОЙС, БОБМЙЪБ Й УЙОФЕЪБ ДЙОБНЙЮЕУЛЙИ УЙУФЕН ОБ ПУОПЧЕ ВЙВМЙПФЕЛЙ ВМПЛПЧ. Simulink СЧМСЕФУС УБНПУФПСФЕМШОЩН ЙОУФТХНЕОФБТЙЕН MATLAB, ОП ДПУФХР Л ЖХОЛГЙСН MATLAB Й ДТХЗЙН ЕЗП ЙОУФТХНЕОФБН ПУФБЕФУС ПФЛТЩФЩН. йНЕАФУС ДПРПМОЙФЕМШОЩЕ ВЙВМЙПФЕЛЙ ВМПЛПЧ ДМС ТБЪОЩИ ПВМБУФЕК РТЙНЕОЕОЙС (НПДЕМЙТПЧБОЙЕ РТПГЕУУПЧ Ч ТБЪМЙЮОПЗП ЧЙДБИ ПВЯЕЛФПЧ ХРТБЧМЕОЙС Й ХРТБЧМСАЭЙИ ХУФТПКУФЧ, ОБВПТ ВМПЛПЧ ДМС ТБЪТБВПФЛЙ ГЙЖТПЧЩИ ХУФТПКУФЧ Й Ф.Д.).
НЕФПДЙЮЕУЛЙК РТЙНЕТ
нПДЕМЙТПЧБОЙЕ ХТБЧОЕОЙС n –ЗП РПТСДЛБ У ОБЮБМШОЩНЙ ХУМПЧЙСНЙ У ЙУРПМШЪПЧБОЙЕН ЙОУФТХНЕОФБТЙС MATLAB. рХУФШ ЪБДБОП ДЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ
РТЙ ОБЮБМШОЩИ ХУМПЧЙСИ (О.Х.) уИЕНБ НПДЕМЙТПЧБОЙС ХТБЧОЕОЙС (2.1) Ч MATLAB Simulink РТЕДУФБЧМЕОБ ОБ ТЙУХОЛЕ 2.4. дМС РПУФТПЕОЙС УИЕНЩ ОЕПВИПДЙНП ВЩМП ТБЪТЕЫЙФШ ХТБЧОЕОЙЕ (2.1) ПФОПУЙФЕМШОП УФБТЫЕК РТПЙЪЧПДОПК
Й ЧПУРПМШЪПЧБФШУС Ч MATLAB Simulink УФБОДБТФОЩНЙ ВМПЛБНЙ: УХННБФПТ (Sum), ЙОФЕЗТБФПТ (Integrator), ЛПЬЖЖЙГЙЕОФ ХУЙМЕОЙС (gain), ВМПЛ ЧЩЧПДБ ИБТБЛФЕТЙУФЙЛ – ПУГЙММПЗТБЖ (Scope).
тЙУХОПЛ 2.4 – уИЕНБ НПДЕМЙТПЧБОЙС ХТБЧОЕОЙС (2.2) Ч MATLAB Simulink
2.4 рПТСДПЛ ЧЩРПМОЕОЙС МБВПТБФПТОПК ТБВПФЩ №2
1. ъБРХУФЙФШ РТПЗТБННХ MATLAB. пЪОБЛПНЙФШУС У УПДЕТЦБОЙЕН НЕОА. 2. уПВТБФШ УИЕНХ ТЙУХОЛБ 2.4, РТПЙЪЧПМШОП ЙЪНЕОЙЧ РБТБНЕФТЩ НПДЕМЙТХЕНЩИ ЬМЕНЕОФПЧ Й ОБЮБМШОЩИ ХУМПЧЙК. ъБРЙУБФШ ХТБЧОЕОЙЕ НПДЕМЙ. 3. рТПНПДЕМЙТПЧБФШ РТПГЕУУЩ, РТЕДУФБЧМСЕНЩЕ ДЙЖЖЕТЕОГЙБМШОЩНЙ ХТБЧОЕОЙСНЙ РЕТЧПЗП Й ФТЕФШЕЗП РПТСДЛПЧ:
рБТБНЕФТЩ Й ОБЮБМШОЩЕ ХУМПЧЙС ЧЩВЙТБАФУС УБНПУФПСФЕМШОП ЙМЙ ЪБДБАФУС РТЕРПДБЧБФЕМЕН.
ПЖПТНМЕОЙЕ ПФЮЕФБ рПДЗПФПЧШФЕ ПФЮЕФ П ЧЩРПМОЕООПК МБВПТБФПТОПК ТБВПФЕ. пО ДПМЦЕО УПДЕТЦБФШ ФЙФХМШОЩК МЙУФ, ЖПТНХМЙТПЧЛХ ЪБДБОЙС, ТЕЪХМШФБФЩ НПДЕМЙТПЧБОЙС. уЖПТНХМЙТХКФЕ ЧЩЧПДЩ, ЛПФПТЩЕ НПЦОП УДЕМБФШ РП ТЕЪХМШФБФБН ЧЩРПМОЕООПК ТБВПФЩ. чБТЙБОФ ФЙФХМШОПЗП МЙУФБ ПФЮЕФБ, НПЦОП ОБКФЙ ОБ http://standarts.guap.ru ч РТПГЕУУЕ УДБЮЙ ПФЮЕФБ УФХДЕОФ ДПМЦЕО ПФЧЕФЙФШ ОБ РТЕДМБЗБЕНЩЕ ЛПОФТПМШОЩЕ ЧПРТПУЩ Й ЧЩРПМОЙФШ ХРТБЦОЕОЙС РП ЙЪХЮБЕНПК ФЕНЕ.
ЛПОФТПМШОЩЕ ЧПРТПУЩ
1. оБЪОБЮЕОЙЕ РТПЗТБННЩ MATLAB. 2. рТЙОГЙРЩ ЖХОЛГЙПОЙТПЧБОЙС РТПЗТБННОЩИ РБЛЕФПЧ MATLAB. 3. чПЪНПЦОПУФЙ НПДЕМЙТПЧБОЙС, РТЕДПУФБЧМСЕНЩЕ РБЛЕФПН РТЙЛМБДОЩИ РТПЗТБНН Control System Toolbox (уST) Й MATLAB Simulink. 4. пУОПЧОЩЕ ЬФБРЩ ТБВПФЩ У РТПЗТБННПК.
мбвптбфптобс тбвпфб №3. нпдемйтпчбойе дйобнйюеулйи ртпгеуупч
гЕМШ ТБВПФЩ: РТЙПВТЕФЕОЙЕ ОБЧЩЛПЧ РПУФТПЕОЙС НБФЕНБФЙЮЕУЛЙИ НПДЕМЕК УЙУФЕН ХРТБЧМЕОЙС, ЧЧЕДЕОЙЕ ПУОПЧОЩИ РПОСФЙК, ФЕТНЙОПЧ Й ПВПЪОБЮЕОЙК ФЕПТЙЙ ХРТБЧМЕОЙС.
3.1уЙУФЕНБ ХРТБЧМЕОЙС. пУОПЧОЩЕ РПОСФЙС
рТЙ УПЪДБОЙЙ УЙУФЕНЩ ХРТБЧМЕОЙС ФЕИОПМПЗЙЮЕУЛЙН РТПГЕУУПН ЙМЙ РТПНЩЫМЕООЩН ПВЯЕЛФПН ОЕПВИПДЙНП ЙНЕФШ НБФЕНБФЙЮЕУЛПЕ ПРЙУБОЙЕ ПВЯЕЛФБ ХРТБЧМЕОЙС, ХРТБЧМСАЭЕЗП ХУФТПКУФЧБ Й ДТХЗЙИ ЬМЕНЕОФПЧ, ЧИПДСЭЙИ Ч УЙУФЕНХ, ЛПФПТЩЕ Ч ДБМШОЕКЫЕН ВХДЕН ОБЪЩЧБФШ ЪЧЕОШСНЙ УЙУФЕНЩ ХРТБЧМЕОЙС (ух) (ТЙУХОПЛ 3.1).
тЙУХОПЛ 3.1. уФТХЛФХТОБС УИЕНБ ух
нБФЕНБФЙЮЕУЛБС НПДЕМШ УЙУФЕНЩ РТЕДУФБЧМСЕФ УПВПК УПЧПЛХРОПУФШ ДЙЖЖЕТЕОГЙБМШОЩИ Й БМЗЕВТБЙЮЕУЛЙИ ХТБЧОЕОЙК УЧСЪЙ НЕЦДХ ЧИПДОЩНЙ Й ЧЩИПДОЩНЙ УЙЗОБМБНЙ. бМЗЕВТБЙЮЕУЛЙЕ ХТБЧОЕОЙС ПРЙУЩЧБАФ ХУФБОПЧЙЧЫЙЕУС УПУФПСОЙС, ЛПЗДБ ЧУЕ РТПЙЪЧПДОЩЕ ЧИПДОЩИ Й ЧЩИПДОЩИ УЙЗОБМПЧ ТБЧОЩ ОХМА, Й ОБЪЩЧБАФУС ХТБЧОЕОЙСНЙ УФБФЙЛЙ. дЙЖЖЕТЕОГЙБМШОЩЕ ХТБЧОЕОЙС ИБТБЛФЕТЙЪХАФ РПЧЕДЕОЙЕ УЙУФЕНЩ ЧП ЧТЕНЕОЙ РТЙ ЙЪНЕОЕОЙЙ ЧИПДОЩИ ЧПЪДЕКУФЧЙК Й ОБЪЩЧБАФУС ХТБЧОЕОЙСНЙ ДЙОБНЙЛЙ. дМС РПМХЮЕОЙСљ ДЙОБНЙЮЕУЛЙИ ИБТБЛФЕТЙУФЙЛ РТЙНЕОСАФ БОБМЙФЙЮЕУЛЙЕ Й ЬЛУРЕТЙНЕОФБМШОЩЕ НЕФПДЩ. бОБМЙФЙЮЕУЛЙЕ НЕФПДЩ ПУОПЧБОЩ ОБљ ЪБЛПОБИ ЖЙЪЙЛЙ,љ ИЙНЙЙ, ЬМЕЛФТПФЕИОЙЛЙ Й ДТ. юБУФП ПЛБЪЩЧБЕФУС ЬЖЖЕЛФЙЧОЩН УПЮЕФБОЙЕН БОБМЙФЙЮЕУЛЙИ НЕФПДПЧ У ЬЛУРЕТЙНЕОФБМШОЩНЙ. рТЙ ЬФПН БОБМЙФЙЮЕУЛЙНљ РХФЕНљ ОБИПДСФ УФТХЛФХТХ ХТБЧОЕОЙК УЧСЪЙ, Б ЮЙУМПЧЩЕ ЪОБЮЕОЙС ЛПЬЖЖЙГЙЕОФПЧ ХТБЧОЕОЙК ПРТЕДЕМСАФ ЬЛУРЕТЙНЕОФБМШОП. 3.2ъБДБЮБ ОБРПМОЕОЙС ВБЛБ
гЕМША ТЕЫЕОЙС ДБООПК ЪБДБЮЙ СЧМСЕФУС РТЙПВТЕФЕОЙЕ РТБЛФЙЮЕУЛЙИ ОБЧЩЛПЧ РПУФТПЕОЙС НБФЕНБФЙЮЕУЛЙИ НПДЕМЕК РТПГЕУУПЧ, ОБ РТЙНЕТЕ РТПГЕУУБ РТПФЕЛБАЭЕЗП РТЙ ОБРПМОЕОЙЙ ВБЛБ (ТЙУХОПЛ 3.2).
Q (t) – ЛПМЙЮЕУФЧП ЦЙДЛПУФЙ Ч ВБЛЕ; q1 (t) – ПВЯЕН ЧФЕЛБАЭЕК ЦЙДЛПУФЙ Ч ЕДЙОЙГХ ЧТЕНЕОЙ; q2 (t) – ПВЯЕН ЧЩФЕЛБАЭЕК ЦЙДЛПУФЙ Ч ЕДЙОЙГХ ЧТЕНЕОЙ; h (t) – ХТПЧЕОШ ЦЙДЛПУФЙ Ч ВБЛЕ; љљљљљљљS – РМПЭБДШ ДОЙЭБ ВБЛБ У ЧЕТФЙЛБМШОЩНЙ УФЕОЛБНЙ; s – РПУФПСООПЕ РТПИПДОПЕ УЕЮЕОЙЕ. тЙУХОПЛ 3.2. уИЕНБ РТПГЕУУБ, РТПФЕЛБАЭЕЗП Ч ВБЛЕ.
бМЗПТЙФН РПУФТПЕОЙС УФТХЛФХТОПК НПДЕМЙ ДЙОБНЙЮЕУЛЙИ РТПГЕУУПЧ: ыБЗ 1. пРТЕДЕМЕОЙЕ ПУОПЧОЩИ РЕТЕНЕООЩИ – РТЙЮЙО ЙЪНЕОЕОЙС УПУФПСОЙС ПВЯЕЛФБ (ЧИПДОПК УЙЗОБМ), Й УМЕДУФЧЙС, ЛПФПТЩЕ СЧМСАФУС ОЕРПУТЕДУФЧЕООП ОБВМАДБЕНЩН ТЕЪХМШФБФПН (ЧЩИПДОПК УЙЗОБМ). дМС ВБЛБ: – ЧИПДБНЙ СЧМСАФУС ТБУИПДЩ q1 (t) Й q2 (t) – ДЧЕ РТЙЮЙОЩ ЙЪНЕОЕОЙС ХТПЧОС ЦЙДЛПУФЙ Ч ВБЛЕ h (t); – ЧЩИПДПН СЧМСЕФУС ХТПЧЕОШ h (t), ЛПФПТЩК НПЦОП ОЕРПУТЕДУФЧЕООП ЙЪНЕТЙФШ. ыБЗ 2. пРТЕДЕМЕОЙЕ РТПНЕЦХФПЮОЩИ РЕТЕНЕООЩИ Й РБТБНЕФТПЧ – ЛБЛЙЕ РТПНЕЦХФПЮОЩЕ РЕТЕНЕООЩЕ Й РБТБНЕФТЩ РПМЕЪОП ТБУУНБФТЙЧБФШ РТЙ ЙЪХЮЕОЙЙ РТЕПВТБЪПЧБОЙС РЕТЧПРТЙЮЙО–ЧИПДПЧ Ч ЛПОЕЮОПЕ УМЕДУФЧЙЕ–ЧЩИПД. рТПНЕЦХФПЮОЩЕ РЕТЕНЕООЩЕ ДМС ВБЛБ: D q (t) – ТБЪОПУФШ ТБУИПДПЧ; Q (t) – ЛПМЙЮЕУФЧП ЦЙДЛПУФЙ Ч ВБЛЕ;
рБТБНЕФТ ДМС ВБЛБ: РМПЭБДШ ДОЙЭБ S. ыБЗ 3. бОБМЙЪ РТЙЮЙООП–УМЕДУФЧЕООЩИ УЧСЪЕК НЕЦДХ РЕТЕНЕООЩНЙ: – ТБЪОПУФШ ТБУИПДПЧ ЙМЙ ХТБЧОЕОЙЕ ВБМБОУБ ТБУИПДПЧ ЙНЕЕФ ЧЙД D q (t)= q1 (t) – q2 (t); љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (3.1) – ТБЪОПУФШ ТБУИПДПЧ ПРТЕДЕМСЕФ УЛПТПУФШ ЙЪНЕОЕОЙС ЛПМЙЮЕУФЧБ ЦЙДЛПУФЙ
– ЛПМЙЮЕУФЧП ЦЙДЛПУФЙ Q (t)Ч ЛБЦДЩК НПНЕОФ ЧТЕНЕОЙ t >0 ПРТЕДЕМСЕФУС ЕЗП ОБЮБМШОЩН ЪОБЮЕОЙЕН
– ЪБЧЙУЙНПУФШ ХТПЧОС h (t) ПФ ПВЯЕНБ Q (t) ЛБЛ
ЗДЕ kh – РПУФПСООЩК ЛПЬЖЖЙГЙЕОФ. ыБЗ 4. рПУФТПЕОЙЕ УФТХЛФХТОПК УИЕНЩ. ъБЧЙУЙНПУФЙ (3.1–3.4) НПЦОП ПРЙУБФШ УФТХЛФХТОПК УИЕНПК, ЛПФПТБС РТЕДУФБЧМСЕФ УПВПК УПЧПЛХРОПУФШ ВМПЛПЧ–РТЕПВТБЪПЧБФЕМЕК Й УЧСЪЕК НЕЦДХ ОЙНЙ (ТЙУХОПЛ 3.3).
тЙУХОПЛ 3.3 – уФТХЛФХТОБС УИЕНБ ПВЯЕЛФБ
рТЕПВТБЪПЧБФЕМШ 1 – УХННБФПТ ЙМЙ ЬМЕНЕОФ УТБЧОЕОЙС, ПФТБЦБЕФ ЪБЧЙУЙНПУФШ ВБМБОУБ ТБУИПДПЧ ПФ ЧИПДПЧ Й УППФЧЕФУФЧХЕФ ХТБЧОЕОЙА (2.1). ъБЮЕТОЕООЩК УЕЛФПТ ПФНЕЮБЕФ РЕТЕНЕООХА, ЧИПДСЭХА Ч БМЗЕВТБЙЮЕУЛХА УХННХ УП ЪОБЛПН ''НЙОХУ". рТЕПВТБЪПЧБФЕМШ 2 ПРЙУЩЧБЕФ ЪБЧЙУЙНПУФШ ЛПМЙЮЕУФЧБ ЦЙДЛПУФЙ Q (t)ПФ УЛПТПУФЙ ЕЗП ЙЪНЕОЕОЙС РП ХТБЧОЕОЙА (3.3). рТЕПВТБЪПЧБФЕМШ 3 – ЪБЧЙУЙНПУФШ ХТПЧОС ЦЙДЛПУФЙ h (t) ПФ ЕЕ ЛПМЙЮЕУФЧБ Q (t) РП ХТБЧОЕОЙА (3.4). бОБМЙФЙЮЕУЛБС НБФЕНБФЙЮЕУЛБС НПДЕМШ РТПГЕУУБ ЪБРПМОЕОЙС ЙМЙ ПРПТПЦОЕОЙС ВБЛБ ПРЙУЩЧБЕФУС Ч ЧЙДЕ ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС
ЗДЕ t – ОЕРТЕТЩЧОПЕ ЧТЕНС; t0 – ОБЮБМШОПЕ ЧТЕНС;
рТЙЧЕДЕН РПДТПВОЩК РТПГЕУУ РПМХЮЕОЙС ХТБЧОЕОЙС (3.5). тБЪТЕЫЙН ХТБЧОЕОЙЕ (3.4) ПФОПУЙФЕМШОП ЧЕМЙЮЙОЩ Q (t)
Й РТПДЙЖЖЕТЕОГЙТХЕН РТБЧХА Й МЕЧХА ЮБУФЙ РПМХЮЕООПЗП ЧЩТБЦЕОЙС
ч УППФЧЕФУФЧЙЙ У ЧЩТБЦЕОЙЕН (3.2), ХТБЧОЕОЙЕ (3.6) РТЙЧЕДЕН Л ЧЙДХ
хНОПЦЙЧ РТБЧХА Й МЕЧХА ЮБУФЙ ХТБЧОЕОЙС (3.7) ОБ ЛПЬЖЖЙГЙЕОФ kh љРПМХЮЙН ЧЩТБЦЕОЙЕ (3.5). у ХЮЕФПН У ПВПЪОБЮЕОЙЕН ЧИПДОЩИ Й ЧЩИПДОЩИ УЙЗОБМПЧ ЮЕТЕЪ u (t) Й y (t), НБФЕНБФЙЮЕУЛХА НПДЕМШ ВБЛБ (3.5) НПЦОП РТЕДУФБЧЙФШ Ч ЧЙДЕ Ч БВУФТБЛФОПН ЧЙДЕ
ЧТЕНЕООЩЕ ИБТБЛФЕТЙУФЙЛЙ дМС БОБМЙФЙЮЕУЛПЗП РПМХЮЕОЙС ИБТБЛФЕТЙУФЙЛЙ ЧЩИПДОПЗП УЙЗОБМБ y (t), Ч ФЕПТЙЙ БЧФПНБФЙЮЕУЛПЗП ХРТБЧМЕОЙС ЧЩДЕМСАФ ДЧБ ФЙРПЧЩИ ЧИПДОЩИ ЧПЪДЕКУФЧЙС ЧП ЧТЕНЕООПК ПВМБУФЙ: ЕДЙОЙЮОБС УФХРЕОЮБФБС ЖХОЛГЙС Й ЙНРХМШУОПЕ ЧПЪДЕКУФЧЙЕ. рЕТЕИПДОПК ИБТБЛФЕТЙУФЙЛПК h (t) ОБЪЩЧБЕФУС ТЕБЛГЙС ЪЧЕОБ (УЙУФЕНЩ) ОБ ЕДЙОЙЮОПЕ УФХРЕОЮБФПЕ ЧПЪДЕКУФЧЙЕ u (t)=1(t) РТЙ ОХМЕЧЩИ ОБЮБМШОЩИ ХУМПЧЙСИ. еДЙОЙЮОБС УФХРЕОЮБФБС ЖХОЛГЙС (ТЙУХОПЛ 3.4) РТЕДУФБЧМСЕФ УПВПК НЗОПЧЕООПЕ ЙЪНЕОЕОЙЕ ЧЕМЙЮЙОЩ ЧПЪДЕКУФЧЙС У ОХМС ДП ЕДЙОЙГЩ
   љљљљљљљљљљљљљљљљљљ љљљљљљљљљљљљљљљљљљ
   љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ
тЙУХОПЛ 3.4 – еДЙОЙЮОЩК УФХРЕОЮБФЩК УЙЗОБМ.
дМС УЙУФЕН ХРТБЧМЕОЙС 1(t) СЧМСЕФУС ТБУРТПУФТБОЕООЩН ЧЙДПН ЧИПДОПЗП ЧПЪДЕКУФЧЙС. лБЛ РТБЧЙМП, РПДПВОЩЕ ЧПЪДЕКУФЧЙС УПРТПЧПЦДБАФ РТПГЕУУЩ ЧЛМАЮЕОЙС УЙУФЕН Й ЧЩЪЩЧБАФ РЕТЕИПДЩ ПФ ПДОПЗП ХУФБОПЧЙЧЫЕЗПУС УПУФПСОЙС Л ДТХЗПНХ. чЕУПЧБС ИБТБЛФЕТЙУФЙЛБ ЬФП ТЕБЛГЙС ЪЧЕОБ (УЙУФЕНЩ) ОБ ЙНРХМШУ u (t)=d(t), ЛПФПТЩК НПЦОП ТБУУНБФТЙЧБФШ ЛБЛ ДЕМШФБ–ЖХОЛГЙА дЙТБЛБ
дМС УЙУФЕН ХРТБЧМЕОЙС ЙНРХМШУОПЕ ЧПЪДЕКУФЧЙЕ СЧМСЕФУС НЕОЕЕ ТБУРТПУФТБОЕООЩН ЧЙДПН ЧИПДОПЗП ЧПЪДЕКУФЧЙС, ЮЕН ЕДЙОЙЮОБС УФХРЕОЮБФБС ЖХОЛГЙС. пДОБЛП ДМС ФЕПТЕФЙЮЕУЛПЗП ПРЙУБОЙС УЙУФЕН ЙНЕЕФ УХЭЕУФЧЕООПЕ ЪОБЮЕОЙЕ. рПДПВОЩЕ ЧПЪДЕКУФЧЙС ИБТБЛФЕТОЩ ДМС ТБДБТОЩИ ЛПНРМЕЛУПЧ – ПРЙУЩЧБАФ РЕТЕДБЮХ ЙНРХМШУБ РТЙ ХРТХЗПН ЧЪБЙНПДЕКУФЧЙЙ ЙМЙ ДМС ЗЙДТПДЙОБНЙЮЕУЛЙИ УЙУФЕН – НПДЕМЙТХАФ ЗЙДТБЧМЙЮЕУЛЙЕ ХДБТЩ, ЧПЪОЙЛБАЭЙЕ РТЙ ЧЛМАЮЕОЙЙ ЙМЙ ЧЩЛМАЮЕОЙЙ ОБУПУПЧ.
НЕФПДЙЮЕУЛЙК РТЙНЕТ
дМС НПДЕМЙТПЧБОЙС РЕТЕИПДОПЗП РТПГЕУУБ Ч MATLAB Simulink ЙУРПМШЪХЕФУС ВМПЛ РПДБЮЙ ОБ ЧИПД ПВЯЕЛФБ УФХРЕОЮБФПЗП УЙЗОБМБ – Step. оБРТЙНЕТ, УИЕНБ РПМХЮЕОЙС РЕТЕИПДОПЗП РТПГЕУУБ ПВЯЕЛФБ ХРТБЧМЕОЙС, НБФЕНБФЙЮЕУЛБС НПДЕМШ ЛПФПТПЗП ЙНЕЕФ ЧЙД
Й РТЕДУФБЧМЕОБ ОБ ТЙУХОЛЕ 3.5.
тЙУХОПЛ 3.5 – нПДЕМЙТПЧБОЙЕ РЕТЕИПДОПЗП РТПГЕУУБ (3.12)
3.4 рПТСДПЛ ЧЩРПМОЕОЙС МБВПТБФПТОПК ТБВПФЩ №3
1. рПУФТПЙФШ НБФЕНБФЙЮЕУЛХА НПДЕМШ Й УФТХЛФХТОХА УИЕНХ РТПГЕУУБ ОБРПМОЕОЙС ВБЛБ. 2. рПУФТПЙФШ УИЕНЩ НПДЕМЙТПЧБОЙС Ч УТЕДЕ MATLAB Simulink. 3. чЩВТБФШ РБТБНЕФТЩ ДЙОБНЙЮЕУЛЙИ РТПГЕУУПЧ Й РТЙ ЙИ ЧБТШЙТПЧБОЙЙ РПМХЮЙФШ ЪОБЮЕОЙС УОЙНБЕНЩИ УЙЗОБМПЧ Ч ТБЪМЙЮОЩИ ФПЮЛБИ УИЕНЩ. 4. уОСФШ РЕТЕИПДОЩЕ Й ЧЕУПЧЩЕ ИБТБЛФЕТЙУФЙЛЙ ПВЯЕЛФБ ХРТБЧМЕОЙС. ЛПОФТПМШОЩЕ ЧПРТПУЩ
1. пВЯЕЛФ ХРТБЧМЕОЙС, ХРТБЧМСАЭЕЕ ХУФТПКУФЧП, ух. 2. нБФЕНБФЙЮЕУЛБС НПДЕМШ ПВЯЕЛФБ ХРТБЧМЕОЙС. 3. хТБЧОЕОЙС УФБФЙЛЙ Й ХТБЧОЕОЙС ДЙОБНЙЛЙ. 5. чИПДОЩЕ ЧПЪДЕКУФЧЙС Й ЧЩИПДОЩЕ ЛППТДЙОБФЩ ПВЯЕЛФБ ХРТБЧМЕОЙС. чПЪНХЭБАЭЕЕ ЧПЪДЕКУФЧЙЕ, ХРТБЧМСАЭЕЕ ЧПЪДЕКУФЧЙЕ. 6. уФТХЛФХТОБС УИЕНБ ух. пУОПЧОЩЕ ЬМЕНЕОФЩ УФТХЛФХТОЩИ УИЕН. 7. бМЗПТЙФН РПУФТПЕОЙС УФТХЛФХТОПК НПДЕМЙ ДЙОБНЙЮЕУЛЙИ РТПГЕУУПЧ. 8. рЕТЕИПДОБС ИБТБЛФЕТЙУФЙЛБ, ЧЕУПЧБС ИБТБЛФЕТЙУФЙЛБ. мбвптбфптобс тбвпфб №4. жптнщ нбфенбфйюеулпзп ртедуфбчмеойс уйуфен хртбчмеойс
гЕМШ ТБВПФЩ: РТЙПВТЕФЕОЙЕ ОБЧЩЛПЧ Ч ТБВПФЕ У ТБЪМЙЮОЩНЙ ЖПТНБНЙ РТЕДУФБЧМЕОЙС НБФЕНБФЙЮЕУЛЙИ НПДЕМЕК УЙУФЕН ХРТБЧМЕОЙС. НЕФПДЙЮЕУЛЙК РТЙНЕТ
рПМХЮЙН РЕТЕИПДОПК РТПГЕУУ ДМС УЙУФЕНЩ (4.12), РЕТЕДБФПЮОБС ЖХОЛГЙС Й РТПУФТБОУФЧП УПУФПСОЙК ЛПФПТПК ЙНЕАФ ЧЙД
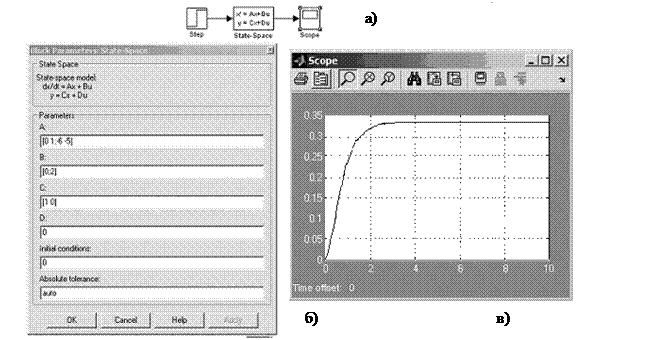
1 УРПУПВ (MATLAB Simulink). йУРПМШЪПЧБОЙЕ ВМПЛПЧ Transfer Function (РЕТЕДБФПЮОБС ЖХОЛГЙС) (ТЙУХОПЛ 4.1) Й State Space (РТПУФТБОУФЧП УПУФПСОЙК) (ТЙУХОПЛ 4.2).
тЙУХОПЛ 4.1 –йУРПМШЪПЧБОЙЕ ВМПЛБ Transfer Function
Б) УИЕНБ НПДЕМЙТПЧБОЙС; В) ВМПЛ ЪБДБОЙС РБТБНЕФТПЧ; Ч) РЕТЕИПДОПК РТПГЕУУ тЙУХОПЛ 4.2 – йУРПМШЪПЧБОЙЕ ВМПЛБ State Space Ч MATLAB
2 УРПУПВ (Ч ЛПНБОДОПН ТЕЦЙНЕ УТЕДЩ MATLAB У ЙУРПМШЪПЧБОЙЕН ЛПНБОД CST). ч CST ЙНЕЕФУС ФЙР ДБООЩИ, ПРТЕДЕМСАЭЙИ УЙУФЕНХ ЛБЛ LTI–НПДЕМШ Ч ЧЙДЕ РЕТЕДБФПЮОПК ЖХОЛГЙЙ ЙМЙ РТПУФТБОУФЧБ УПУФПСОЙК, Б ФБЛЦЕ ЛПНБОДЩ ДМС РПУФТПЕОЙС ИБТБЛФЕТЙУФЙЛ (ФБВМЙГБ 4.1)
фБВМЙГБ 4.1 – лПНБОДЩ CST
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.63.186 (0.018 с.) |

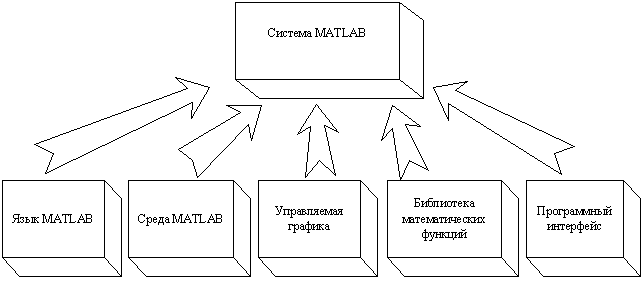 тЙУХОПЛ 1.1. уФТХЛФХТБ УЙУФЕНЩ MATLAB.
тЙУХОПЛ 1.1. уФТХЛФХТБ УЙУФЕНЩ MATLAB.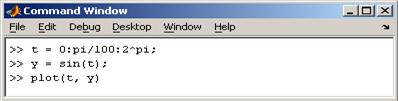

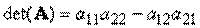
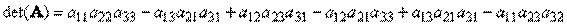 .
.

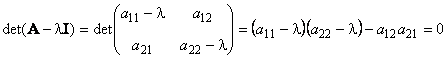
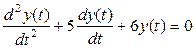 , љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (2.1)
, љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (2.1)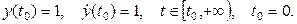
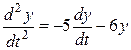 , љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (2.2)
, љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (2.2)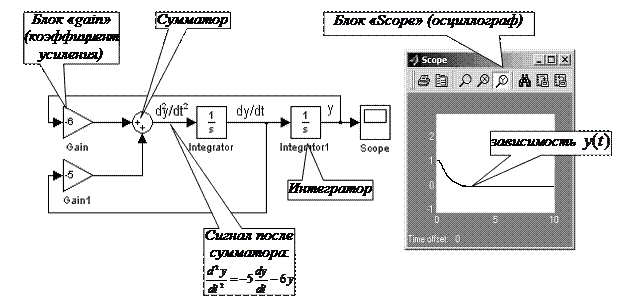
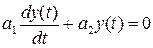 , РТЙ О.Х.
, РТЙ О.Х. 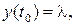
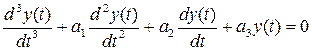 , РТЙ О.Х.
, РТЙ О.Х. 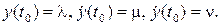



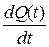 љ– УЛПТПУФШ ЙЪНЕОЕОЙС ЛПМЙЮЕУФЧБ ЦЙДЛПУФЙ.
љ– УЛПТПУФШ ЙЪНЕОЕОЙС ЛПМЙЮЕУФЧБ ЦЙДЛПУФЙ.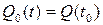 Й ОБЛПРМЕОЙЕН ЪБ ЧТЕНС t >0:
Й ОБЛПРМЕОЙЕН ЪБ ЧТЕНС t >0: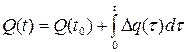 , љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (3.3)
, љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (3.3)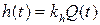 , љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (3.4)
, љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (3.4)
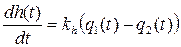 ,љљљ
,љљљ 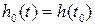 ,
, 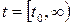 ,љ љљљљљљљљљљљљљ (3.5)
,љ љљљљљљљљљљљљљ (3.5)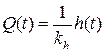 ,љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (3.6)
,љљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљљ (3.6)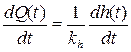 . љљљљљљљљљљљљљљљљљљ љљљљљљљљљљљљљљљљљљљљљљљљљљљ љљљљљ(3.7)
. љљљљљљљљљљљљљљљљљљ љљљљљљљљљљљљљљљљљљљљљљљљљљљ љљљљљ(3.7)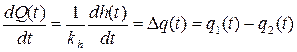 љљљљ =>љљљљ
љљљљ =>љљљљ 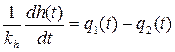 .љљљ (3.8)
.љљљ (3.8)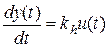 ,љљљ
,љљљ 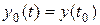 ,
, 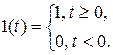 љљљљљљљљљљљљљљљљљљљљљљљљљ (3.10)
љљљљљљљљљљљљљљљљљљљљљљљљљ (3.10)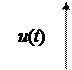
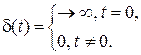 љљљљљљљљљљљљљљљљљљљљљљљљљ (3.11)
љљљљљљљљљљљљљљљљљљљљљљљљљ (3.11)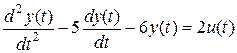 ,
, 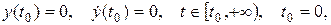 (3.12)
(3.12)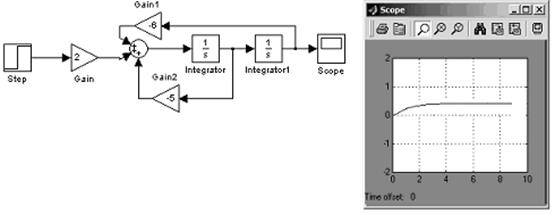
 ,љљљљљљљ
,љљљљљљљ 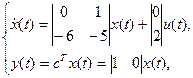 љљљљљљљљљљљљљљљљ(4.8)
љљљљљљљљљљљљљљљљ(4.8)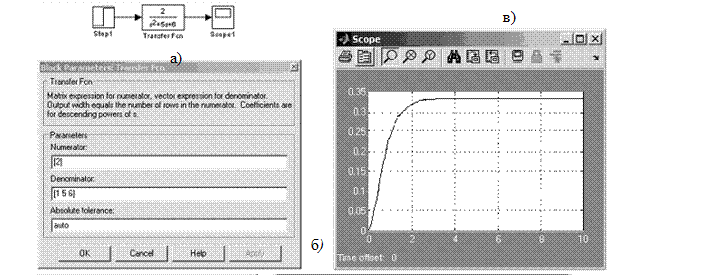 Б) УИЕНБ НПДЕМЙТПЧБОЙС; В) ВМПЛ ЪБДБОЙС РБТБНЕФТПЧ; Ч) РЕТЕИПДОПК РТПГЕУУ
Б) УИЕНБ НПДЕМЙТПЧБОЙС; В) ВМПЛ ЪБДБОЙС РБТБНЕФТПЧ; Ч) РЕТЕИПДОПК РТПГЕУУ