
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
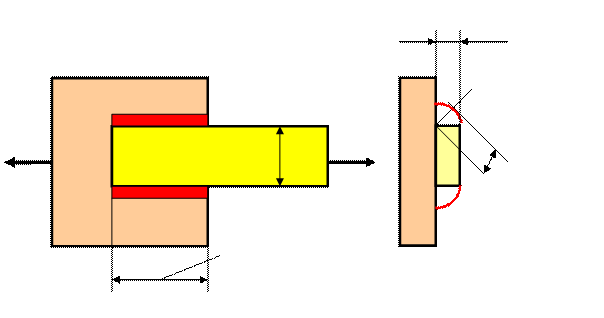
Задача №1. Расчет болтового соединения.Стр 1 из 3Следующая ⇒
Определить, исходя из условий прочности на срез и смятие необходимый диаметр болта в соединении, если известно:
F/2 t1
а а F/2 t1 t2 F в в
Рис.6 Таблица 6 Исходные данные для решения задачи №1
Алгоритм решения задачи №1: 1) Т.к. болт работает на срез одновременно по двум сечениям – аа и вв, то площадь среза равна Аср = πd2/2,см2 по условию прочности А ср ≥ F [τср], см2 __________ тогда диаметр болта равен d ≥√ 2F/ π[τср], см 2) Если 2t1≥ t2, то опасной с точки зрения смятия будет внутренняя деталь, тогда Асм = d t2,см2 А см = F / [σсм], см2 Тогда диаметр болта равен d ≥ F / [σсм] t2 , см Если 2t1≤ t2, тогда диаметр болта равен d ≥ F / [σсм] 2t1 , см 3) Из двух значений диаметра, найденных по условиям прочности на срез и смятие, предпочтение отдаем б о льшему, и окончательно назначаем диаметр болта по ГОСТу. 4) Записать вывод и указать диаметр болта на чертеже Задача №2. Спроектировать равнопрочное соединение с фланговыми швами (по вариантам) Rwf = 18 кн/см2 Таблица 7 -Исходные данные для решения задачи №2
t
F b F 0,7кf
Lфл
Рис.7 Алгоритм решения задачи №2: 1) Выполнить эскиз соединения 2) Найти допускаемое усилие Fдоп = А Rу= b * t * Rу, кн 3) Назначить катет шва Кf ≤ t, см (кмин = 4 мм) 4) Определить суммарную длину углового шва ΣLw ≥ Fдоп / 0,7кf Rwf, см 5) Определить необходимую длину флангового шва Lфл = ΣLw / 2, см Длина шва не должна превышать 60 к Lфл ≤ 60к и не должна быть меньше 40 мм 6) Ответ: Lфл = … см ≤ 60к
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. При действии каких сил возникает деформация сдвига? 2. Какие напряжения возникают при деформации сдвига? 3. Что называется смятием? 4. Какие напряжения возникают при смятии? 5. Как направлены лобовые швы нахлесточного соединения по отношению к действующей нагрузке? 6. Как направлены фланговые швы нахлесточного соединения по отношению к действующей нагрузке? 7. Что такое катет шва? От чего он зависит? 8. Что такое равнопрочность сварного соединения? РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №7 (РГР №7) Тема: Геометрические характеристики плоских сечений Цель работы: научиться определять главные центральные моменты инерции для сечений, имеющих ось симметрии
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ · Момент инерции сложной фигуры является суммой моментов инерции частей, на которые её разбивают · Моменты инерции вырезов и отверстий имеют отрицательную величину · Моменты инерции частей, чьи главные оси не совпадают с центральными осями сечения в целом, пересчитывают с помощью формулы для моментов инерции относительно параллельных осей Jх = Jх0 + А а2, где а – расстояние между осями 0х и 0х0 · Моменты инерции стандартных профилей определяются по сортаментам. Для полосовой стали использовать формулы для прямоугольника
ПРАКТИЧЕСКАЯ ЧАСТЬ Задача №1. Определить геометрические характеристики плоских фигур.
d х0 h1 a H h3 h2 х h1
b1 b2
Рис.8
Таблица 8
Исходные данные для решения задачи №1
Задача №2. Определить центральные моменты инерции сечения в соответствии с вариантом расчетно-графической работы №3 «Центр тяжести». Алгоритм решения задач: 1) Определяем геометрические характеристики простых сечений (круга, прямоугольника) для круглого сечения А= πd2/4, см2 Jх = Jу = πd4/64,см4 для прямоугольного сечения А= b h, см2 Jх = b h3/ 12,см4 Jy = b3 h/ 12,см4 Для сечений, составленных из прокатного профиля, геометрические характеристики определяем по сортаменту. 2) Устанавливаем координаты центров тяжести простых фигур, для чего проведем центральные оси для каждой простой фигуры 3) Проводим главные центральные оси, которые проходят через центр тяжести всего сечения 3) Определяем главные моменты инерции сечения, как сумму моментов инерции простых фигур используя формулу моментов инерции относительно параллельных осей Примеры определения главных моментов инерции сечения приведены на стр.140-143 Сетков В.И. «Сборник задач по технической механике» М.: «Академия», 2007г
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какие оси называются центральными? 2. Какие оси называются главными центральными? 3. В чем измеряется момент инерции сечения? 4. Как обозначается балка двутавровая? 5. Что обозначает № швеллера? 6. Диаметр сплошного вала увеличили в 2 раза. Во сколько раз увеличится осевой момент инерции?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 1121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.130.31 (0.027 с.) |
 [τср] =13 кн/см2 db [ σсм ]=26 кн/см2
[τср] =13 кн/см2 db [ σсм ]=26 кн/см2
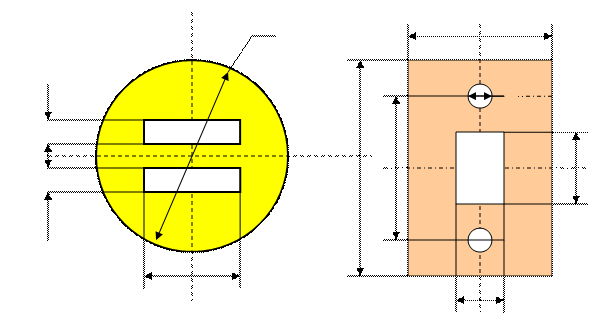 у D B
у D B


