
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории матричных игр.Содержание книги
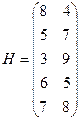
Поиск на нашем сайте a) Найти решение игры, если сторона А располагает пятью стратегиями А1, А2, А3, А4 и А5, сторона В – двумя В1 и В2. Матрица игры имеет вид:
Решение. Платежную матрицу игры можно записать в виде:
Проверим, имеет игра решение в чистых стратегиях или нет. Для этого найдем максимин m и минимакс M.
Получили, что Матрица игры имеет размерность
Выделим верхнюю границу выигрыша для игрока А. Это будет ломаная А1КА4. Отрезок KN определяет цену игры Активными стратегиями игрока А являются стратегии А1 и А4, тогда Тогда игра сводится к игре с матрицей Уравнения, из которых определяются
Отсюда: Уравнения, из которых определяются
Отсюда: Задача решена. Смешанная стратегия игрока А: b) Сторона А посылает в район расположения противника В два бомбардировщика I и II; I летит спереди, II - сзади. Один из бомбардировщиков— заранее неизвестно какой — должен нести бомбу, другой выполняет функцию сопровождения. В районе противника бомбардировщики подвергаются нападению истребителя стороны В. Бомбардировщики вооружены пушками различной скорострельности. Если истребитель атакует задний бомбардировщик II, то по нему ведут огонь пушки только этого бомбардировщика; если же он атакует передний бомбардировщик, то по нему ведут огонь пушки обоих бомбардировщиков. Вероятность поражения истребителя в первом случае 0,3, во втором 0,7. Если истребитель не сбит оборонительным огнем бомбардировщиков, то он поражает выбранную им цель с вероятностью 0,6. Задача бомбардировщиков — донести бомбу до цели; задача истребителя — воспрепятствовать этому, т. е. сбить бомбардировщик-носитель. Требуется выбрать оптимальные стратегии сторон: а) для стороны А: какой бомбардировщик сделать носителем? 6) для стороны В: какой бомбардировщик атаковать? Решение. Имеем простой случай игры 2x2; выигрыш— вероятность непоражения носителя. Наши стратегии: А1 — носитель — бомбардировщик I; А2 — носитель — бомбардировщик II. Стратегии противника: В1 — атакуется бомбардировщик I; В2 — атакуется бомбардировщик II. Составим матрицу игры, т. е. найдем средний выигрыш при каждой комбинации стратегий. 1. А1В1 (носитель I, атакуется I). Носитель не будет поражен, если бомбардировщики собьют истребитель, или не собьют, но он не поразит свою цель: a11 = 0,7 + 0,3.0,4 = 0,82. 2. А2В1 (носитель II, атакуется I): a21=1. 3. А1В2 (носитель I, атакуется II): а12 = 1. 4. А2В2 (носитель II, атакуется II): a22 = 0,3 + 0,7 • 0,4 = 0,58. Матрица игры имеет вид:
Нижняя цена игры 0,82; верхняя цена 1. Матрица не имеет седловой точки; решение ищем в области смешанных стратегий. Имеем:
Отсюда Зная v, определяем q1 и q2 — частоты стратегий B1 и В2 в оптимальной стратегии противника.Имеем: откуда Задача решена. Смешанная стратегия игрока А: c) Сторона А нападает на объект, сторона B — обороняет его. У стороны А — два самолета; у стороны B — три зенитных орудия. Каждый самолет является носителем мощного поражающего средства; для того чтобы объект был поражен, достаточно, чтобы к нему прорвался хотя бы один самолет. Самолеты стороны А могут выбирать для подхода к объекту любое из трех направлений: I, II, III. Противник (сторона В) может разместить любое из своих орудий на любом направлении; при этом каждое орудие простреливает только область пространства, относящуюся к данному направлению, и не простреливает соседних направлений. Каждое орудие может обстрелять только один самолет; обстрелянный самолет поражается с вероятностью 1. Сторона А не знает, где размещены орудия; сторона В не знает, откуда прилетят самолеты. Задача стороны А — поразить объект; задача стороны В — не допустить его поражения. Найти решение игры. Решение. Игра представляет собой игру 2x3. Выигрыш — вероятность поражения объекта. Наши возможные стратегии: А1 — послать по одному самолету на два различных направления. А2 — послать оба самолета по одному направлению. Стратегии противника: B1— поставить по одному орудию на каждое направление; B2 — поставить два орудия на одно направление и одно — на другое; B3 — поставить все три орудия на одно направление. Составляем матрицу игры. 1. А1В1 (самолеты летят по разным направлениям; орудия расставлены по одному). Очевидно, при этом ни один самолет не прорвется к объекту: 2. A2B1 (самолеты летяг вместе по одному направлению; орудия расставлены по одному). Очевидно, при этом один самолет пройдет к объекту необстрелянным: 3. A1B2 (самолеты летят по одному; противник защищает два направления и оставляет незащищенным третье). Вероятность того, что хотя бы один самолет прорвется к объекту, равна вероятности того, что один из них выберет незащищенное направление: 4. А2В2 (самолеты летят вместе по одному направлению; противник защищает одно направление двумя орудиями и одно — одним, т. е. фактически защищает одно направление и оставляет незащищенным два). Вероятность того, что хотя бы один самолет прорвется к объекту, равна вероятности выбора парой самолетов фактически незащищенного направления: 5. A1B3 (самолеты летят по одному; противник защищает тремя орудиями только одно направление): 6. А2В3 (самолеты летят оба вместе; противник защищает тремя орудиями только одно направление). Чтобы объект был поражен, самолеты должны выбрать незащищенное направление: Матрица игры:
Из матрицы видно, что стратегия В3 является заведомо невыгодной по сравнению с В2 (это можно было решить и заранее). Вычеркиванием стратегии В3 игра сводится к игре 2х2:
Матрица имеет седловую точку: нижняя цена игры -
Заметим, что найденное решение игры не является единственным; помимо решения в чистых стратегиях, существует целый участок смешанных стратегий игрока А, являющихся оптимальными, от  до до 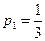 (см. рис.) (см. рис.)
Задачи для самостоятельного решения: d) Найти решение игры, если сторона А располагает двумя стратегиями А1 и А2, сторона В – пятью В1, В2, В3, В4, В5. Матрица игры имеет вид: е) Найти решение игры, если сторона А располагает пятью стратегиями А1, А2, А3, А4 и А5, сторона В – двумя В1 и В2. Матрица игры имеет вид: f) Сторона А располагает двумя стратегиями А1, и А2, сторона В — четырьмя В1, В2, В3 и В4. Матрица игры имеет вид:
Найти решение игры. § 6. Контрольные задания Задание 1 Решить графическим методом следующие задачи линейного программирования. Найти max и min. Сформулировать двойственные задачи. Варианты задания 1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а)
9. а) 10. а) 11. а) 12. а) 13. а) 14. а) 15. а) 16. а) 17. а) 18. а) 19. а) 20. а) 21. а) 22. а)
23. а) 24. а) 25. а) 26. а) Задание 2 Решить симплексным методом Варианты задания 1) 3) 5) 7) 9) 11) 13)
Решить симплекс-методом задачу ЛП, начав с указанного опорного плана и взяв в качестве базисных переменных
Задание 3 Решить симплекс методом задачу ЛП, приведя ее к каноническому виду: Варианты заданий
Задание 4 Решить симплекс-методом задачу ЛП, определив начальный опорный план методом искусственного базиса (см. задачи варианта из задания 1). Задание 5 Транспортная задача Варианты 1-16. Имеется четыре поставщика A1, A2, A3, A4, и четыре потребителя продукции B1, B2, B3, B4, с заданными объемами производства и потребления. Известна стоимость поставки единицы продукции от каждого поставщика каждому потребителю. Определить оптимальные связи поставщиков и потребителей минимизирующие затраты на перевозки. Исходную матрицу составить из таблицы, исключив из нее 3 столбца номера которых указаны в каждом варианте. Исходный план построить а) методом северо-западного угла, б) методом минимальной стоимости.
1) Исключить столбцы 1, 2, 3. 2) Исключить столбцы 1, 2, 4. 3) Исключить столбцы 1, 2, 6. 4) Исключить столбцы 1, 2, 7. 5) Исключить столбцы 1, 3, 4. 6) Исключить столбцы 1, 3, 6. 7) Исключить столбцы 1, 3, 7. 8) Исключить столбцы 1, 4, 6. 9) Исключить столбцы 1, 4, 7. 10) Исключить столбцы 1, 6, 7. 11) Исключить столбцы 2, 3, 4. 12) Исключить столбцы 2, 3, 6. 13) Исключить столбцы 2, 3, 7. 14) Исключить столбцы 3, 4, 6. 15) Исключить столбцы 3, 6, 7. 16) Исключить столбцы 4,6,7. Вариант 17. Имеется четыре поставщика A1, A2, A3, A4, и четыре потребителя продукции B1, B2, B3, B4, B5 с заданными объемами производства и потребления. Известна стоимость поставки единицы продукции от каждого поставщика каждому потребителю. Определить оптимальные связи поставщиков и потребителей минимизирующие затраты на перевозки. Исходный план построить а) методом северо-западного угла,б) методом минимальной стоимости.
Вариант 18. Организация, занимающаяся механизацией трудоемких работ, располагает набором однородных технических средств в количестве 30 единиц, которые размещаются в 3 базах A1, A2, A3..При этом базы A1, A2 имеют по 11 единиц техники, а база A3 - 8 единиц. Использование этой техники планируется на четырех объектах B1, B2, B3, B4. При чем объект B1 нуждается в 5 единицах, объекты B2, B3 – в 9 единицах каждый, а объект B4 – в 7 единицах техники. Эффективность эксплуатации технических средств зависит от того, насколько интенсивно они используются, т.е. чем меньше простои, тем выше эффективность. Общая картина использования техники с указанием ее наличия в базах и потребностей на объектах показана в таблице. Необходимо разработать такой план распределения машин по объектам, при котором суммарное время простоя техники окажется наименьшим. Исходный план построить а) методом северо-западного угла,б) методом минимальной стоимости.
Вариант 19. Производственное предприятие располагает четырьмя бригадами рабочих-специалистов определенного профиля: условно A1, A2, A3, A4. Специалисты из этих бригад распределяются по пяти различным видам работ: условно B1, B2, B3, B4, B5.. От того, как будут распределены по этим видам рабочие, зависит в первую очередь качество продукции. В качестве стоимостей выступают стоимости бракованной продукции, получаемой при данном распределении рабочих по видам работ. Общая картина наличия рабочих в бригадах и распределение их по конкретным видам работ показана в таблице. Определить оптимальное распределение рабочих по видам работ, при котором стоимость бракованной продукции будет минимальной. Исходный план построить а) методом северо-западного угла, б) методом минимальной стоимости.
Вариант 20. Имеется три поставщика A1, A2, A3, и пять потребителей продукции B1, B2, B3, B4, B5 с заданными объемами производства и потребления. Известна стоимость поставки единицы продукции от каждого поставщика каждому потребителю. Определить оптимальные связи поставщиков и потребителей минимизирующие затраты на перевозки. Исходный план построить а) методом северо-западного угла, б) методом минимальной стоимости.
Варианты 21-26. Имеется четыре поставщика A1, A2, A3, и четыре потребителя продукции B1, B2, B3, B4, B5 с заданными объемами производства и потребления. Известна стоимость поставки единицы продукции от каждого поставщика каждому потребителю. Определить оптимальные связи поставщиков и потребителей минимизирующие затраты на перевозки. Исходную матрицу составить из таблицы, исключив из нее 3 столбца номера которых указаны в каждом варианте. Исходный план построить а) методом северо-западного угла, б) методом минимальной стоимости.
21) Исключить столбцы 2, 3. 22) Исключить столбцы 2, 6. 23) Исключить столбцы 2, 7. 24) Исключить столбцы 3, 6. 25) Исключить столбцы 3, 7. 26) Исключить столбцы 6, 7. Задание 6
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1019; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |



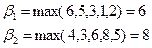 ,
,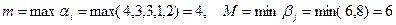 .
. , значит седловых точек нет, поэтому игра не имеет решения в чистых стратегиях. Найдем решение игры в смешанных стратегиях.
, значит седловых точек нет, поэтому игра не имеет решения в чистых стратегиях. Найдем решение игры в смешанных стратегиях. , можно найти решение графически. Возьмем на оси абсцисс участок длиной 1. Левый конец будет изображать стратегию В1 игрока В, а правый – стратегию В2. Через точки В1 и В2 проведем перпендикуляры и на них будем откладывать выигрыши при использовании игроком В своих чистых стратегий. На левом перпендикуляре будем откладывать выигрыш при стратегии В1, а на правом выигрыш при использовании стратегии В2. Проводим отрезки, соединяющие точки на левом и правом перпендикулярах, соответствующие стратегиям игрока А.
, можно найти решение графически. Возьмем на оси абсцисс участок длиной 1. Левый конец будет изображать стратегию В1 игрока В, а правый – стратегию В2. Через точки В1 и В2 проведем перпендикуляры и на них будем откладывать выигрыши при использовании игроком В своих чистых стратегий. На левом перпендикуляре будем откладывать выигрыш при стратегии В1, а на правом выигрыш при использовании стратегии В2. Проводим отрезки, соединяющие точки на левом и правом перпендикулярах, соответствующие стратегиям игрока А.
 , а отрезки B1N и B2N определяют смешанные стратегии игрока В.
, а отрезки B1N и B2N определяют смешанные стратегии игрока В. .
.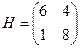 .
.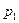 и
и  следующие:
следующие:
 ;
; 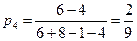 ;
;  .
. и
и  следующие:
следующие:
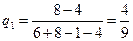 ;
;  ;
;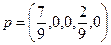 . Смешанная стратегия игрока В:
. Смешанная стратегия игрока В: 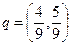 . Цена игры
. Цена игры  .
.
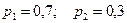 . Цена игры равна
. Цена игры равна  .
. ,
, .
. . Смешанная стратегия игрока В:
. Смешанная стратегия игрока В: 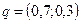 . Цена игры
. Цена игры  .
.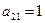 .
.


 .
. .
.
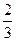 совпадает с верхней. Одновременно замечаем, что для нас (А) стратегия А1 является заведомо невыгодной. Вывод: обе стороны А и В должны пользоваться всегда своими чистыми стратегиями А2 и В2, т. е. мы должны посылать самолеты по 2, выбирая случайным образом направление, по которому посылается пара; противник должен ставить орудия так: два — на одно направление, одно— на другое, причем выбор этих направлений также должен производиться случайно (здесь, как мы видим, уже «чистые стратегии» включают элемент случайности). Применяя эти оптимальные стратегии, мы всегда будем получать постоянный средний выигрыш
совпадает с верхней. Одновременно замечаем, что для нас (А) стратегия А1 является заведомо невыгодной. Вывод: обе стороны А и В должны пользоваться всегда своими чистыми стратегиями А2 и В2, т. е. мы должны посылать самолеты по 2, выбирая случайным образом направление, по которому посылается пара; противник должен ставить орудия так: два — на одно направление, одно— на другое, причем выбор этих направлений также должен производиться случайно (здесь, как мы видим, уже «чистые стратегии» включают элемент случайности). Применяя эти оптимальные стратегии, мы всегда будем получать постоянный средний выигрыш 

 б)
б) 
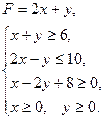 б)
б) 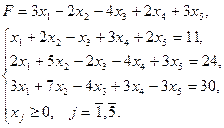
 б)
б) 
 б)
б) 
 б)
б) 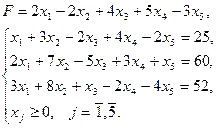
 б)
б) 
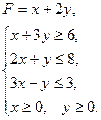 б)
б) 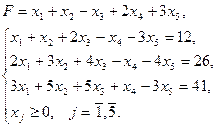
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 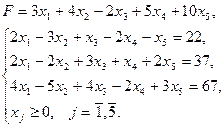
 б)
б) 
 б)
б) 
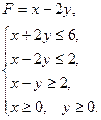 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
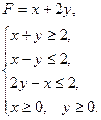 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
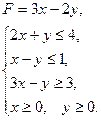 б)
б) 
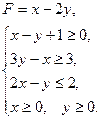 б)
б) 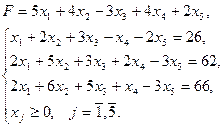
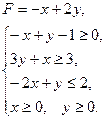 б)
б) 
 2)
2) 
 4)
4) 
 6)
6) 
 8)
8) 
 10)
10) 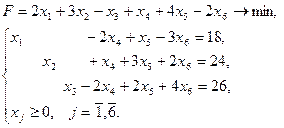
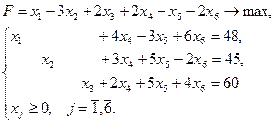 12)
12) 
 .
.




