Часто используемые правила математической логики

not not A = A
not (A and B) = not A or not B
not (A or B) = not A and not B
A or (not A and B) = A or B
True and A = A
True or A = True
False and A = False
False or A = A

Стандартные процедуры и функции

Стандартные функции

abs(x)	|x|
sqr(x)	х^2
sqrt(x)	корень квадратный из х
ln(x)	ln x
exp(x)	е^х
sin(x)	sin x
cos(x)	cos x
arctan(x)	arctan x
int(x)	целая часть х (вещественный результат)
trunc(x)	целая часть х (целый результат)
frac(x)	дробная часть х (вещественный результат)
round(x)	округление вещественного х (целый результат)
Odd(i)	True, если i - нечетно, False в противном случае
sizeof(n)	Размер значения выражения n в байтах. В качестве n может также использоваться имя типа
Pi	возвращает число "пи" = 3.141592...

Пример. sqr(x+y-1)

Стандартные функции в Dephi

Требуется подключение модуля Math: uses Math;

power(x,y)	x^у
arccos(x)
arcsin(x)
sec(x)
cosec(x)
tan(x)
DivMod(x,y,d,m)	d:=x div y; m:=x mod y;
InRange(x,min,max)	min<=x<=max
Hypot(a,b)	гипотенуза треугольника с катетами a, b
log10(x)
logN(N,x)
max(x,y)
min(x,y)

В модуле Math определены также константы

const
MaxDouble = 1.7E308;
MinDouble = 5E-324;

Стандартные процедуры для целых

Inc(x)	x:=x+1
Dec(x)	x:=x-1
Inc(x,n)	x:=x+n
Dec(x,n)	x:=x-n

Явление переполнения

Пример.

var x: real;
begin
x:=MaxDouble;
x:=x*2; // ошибка времени выполнения

Для избежания ошибки переполнения можно воспользоваться директивами процессора {$Q-}, {$Q+}:

var i: integer;
begin
i:=MaxInt;
{$Q-} // отключение контроля за переполнением
i:=i+1;
{$Q+} // включение контроля за переполнением

Погрешность округления и вычислительная погрешность

1.7E8, где после семерки идут еще 15-16 значащих цифр, называемые погрешностью округления.

Вещественные числа представляются в памяти компьютера не точно, а приближенно. Погрешность представления вещественных типов в памяти компьютера называется погрешностью округления. Значения типа real хранят 15-16 значащих цифр, поэтому, например, для числа 1.7 погрешность округления составляет около 1E-16.

При вычислениях погрешность округления может накапливаться; такая погрешность называется вычислительной.

Пример.

x:=0.9-3*0.3 // выведется число 1.11Е-16
x:=(0.9-3*0.3)*1E16 // выведется число 1.11 (вычислительная погрешность)

Правило. Ввиду погрешности округления вещественные числа обычно не сравнивают на равенство.

Неверно:

var x,y: real;
...
if x=y then... // неверно!

Верно:

eps:=1E-14;
if abs(x-y)<eps then...

В Delphi:

if SameValue(x,y,eps) then...

Условный оператор

if логическое выражение then оператор1 [ else оператор2 ]

Семантика оператора if задается следующей блок-схемой:

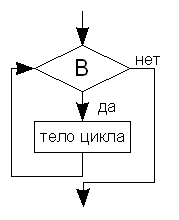
Пример. Hайти min из a, b.

if b>a then
min:=a
else
min:=b;

Пример. Упорядочить значения в a, b по возрастанию.

if a>b then
поменять значения местами

Составной оператор

begin
операторы
end

Необходимость составного оператора: составной оператор объединяет несколько операторов в один:

Пример.

if a>b then
begin
v:=a;
a:=b;
b:=v;
end;

Вложенные условные операторы

В качестве оператора по ветви if или else может быть другой условный оператор.

Пример. Дано x. Найти y, равное 2*x, при x>3, -x, при 1<x<=3 и x*x, при x<1.

if x>3 then
y:=2*x
else if x>1 then
y:=-x
else
y:=x*x;

Правило. еlse относится к ближайшему одинокому if.

if B then
if C then
A1
else A2

Оператор выбора варианта

case перeключатель of
список выбора1: оператор1;
список выбора2: оператор2;
...
список выбораN: операторN;
else оператор0;
end

Списки выбора не должны перекрываться и должны иметь тип, совпадающий с типом выражения-переключателя.

Примечание. Пeреключатель должен быть выражением целого, символьного или перечислимого типа.

Пример.

case DayOfWeek of
1..5: writeln('Будний');
6,7: writeln('Выходной');
else writeln('Ошибка');
end;

Пример.

case Month of
4,6,9,11: DayInMonth:=30;
2: DayInMonth:=28;
else DayInMonth:=31;
end.

Циклы while, repeat и for

Оператор цикла с предусловием (цикл ПОКА)

while B do
оператор

где оператор образует тело цикла, B является логическим выражением.

Семантика оператора while задается следующей блок-схемой:

Оператор цикла с постусловием (цикл ДО)

repeat
операторы
until B

где операторы образуют тело цикла, B является логическим выражением.

Семантика оператора repeat задается следующей блок-схемой:

Сравнение while и repeat

• Тело repeat выполняется по крайней мере 1 раз
• Условия продолжения цикла в while и repeat противоположны
• В repeat можно записывать несколько операторов без использования begin / end

Оператор цикла с параметром

for x:=x1 to x2 do
оператор

или

for x:=x2 downto x1 do
оператор

где переменная x называется параметром цикла, x1 и x2 – выражения совместимого с x типа.

Важно! Выражения x1 и x2 вычисляются один раз до цикла.

Замечания.

1. Значение параметра цикла после выполнения цикла считается неопределенным.
2. В теле цикла нельзя изменять параметр цикла. Например:

for i:=1 to n do
i:=i-1; // ошибка!

for i:=1 to n do
read(i); // ошибка!

for i:=1 to n do
for i:=1 to m do // ошибка!

Определение. Инвариант цикла – это предикат, который истинен перед выполнением цикла и после каждой его итерации. Например, если находится сумма чисел, то инвариант цикла – сумма уже введенных чисел. Если находится минимум, то инвариант цикла: в min – минимальные из уже введенных. Инвариант цикла служит для доказательства правильности алгоритма.