
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема. Дослідження шифраторів, дешифраторів та перетворювачів кодуСодержание книги
Поиск на нашем сайте
Мета роботи – вивчення принципів роботи, методів синтезу та особливостей функціонування найпростіших схем шифраторів, дешифраторів, надбання навичок реалізації їх на реальних інтегральних елементах та побудови комбінаційних схем на їх основі.
Теоретичні відомості про шифратори, дешифратори та перетворювачі коду
Шифратори Шифратор має m входів і n виходів ( На рис. 3.1 зображена структурна схема шифратора з т = 8, п = 3 (входи х0 – х7, виходи y0 – y2, х7 та y2 старші розряди). Наявність додаткового виходу z дозволяє відрізнити нульовий вихідний набір, який відповідає х0 = 1, від ситуації, коли всі вхідні сигнали дорівнюють нулю. В останньому випадку z теж дорівнює нулю. Шифратор реалізує логічні функції
z = x 0 + x 1 + x 2 + x 3 + x 4 + x 5 + x 6+ x 7.
а б Рис. 3.1. Функціональна схема (а) і умовне позначення (б) шифратора.
В обчислювальній техніці знаходять також використання пріоритетні шифратори, вихідний сигнал яких однозначно визначається при наявності декількох вхідних сигналів одночасно, що заборонено в звичайних шифраторах. Таблиці істинності звичайного та пріоритетного шифраторів наведені в табл.3.1 та табл.3.2 відповідно. Таблиця 3.1
Таблиця 3.2
Дешифратори Дешифратор має n входів, т ( Таблиця істинності дешифратора, функціональна схема та умовне позначення на прикладі дешифратора 4*10 (п = 4, т = 10) наведені в табл. 3.3 та на рис. 3.2 відповідно. Дешифратор, для якого т < 2n, називається неповним дешифратором на відміну від повного дешифратора, для якого т = 2n.
а б Рис. 3.2 Умовне позначення (а) та функціональна схема дешифратора (б).
Таблиця 3.3
Для неповного дешифратора набори вхідних сигналів від т до 2n -1 (тобто 1010... 1111) заборонені, тому значення виходів дешифратора на таких наборах невизначені (позначені х). Наведений дешифратор реалізує систему функцій
В умовному позначенні дешифратора (рис. 5) у лівому полі вказуються або номери входів, або їх вага в десятковій системі числення, а в правому – номери виходів, починаючи з нульового до т. Дешифратори використовуються також для синтезу комбінаційних схем. Як приклад побудуємо комбінаційну схему, що реалізує таблицю істинності (табл. 3.4), з допомогою дешифратора 3*8 з інверсними виходами.
Таблиця 3.4
З таблиці 3.4 видно, що функція Z1 має три одиничних набори та 5 нульових. Отже доцільно для її побудови використати ДНФ. Аналогічно для Z2 доцільно використати КНФ. Функції в відповідних формах мають вид:
де y i – інверсні виходи дешифратора.
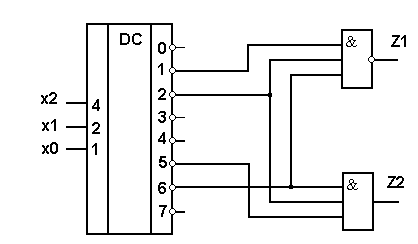
Відповідна схема наведена на рис. 3.3.
Рис. 3.3 Комбінаційна схема на основі дешифратора Перетворювач коду Як приклад розглянемо побудову перетворювача звичайного трьохрозрядного двійкового коду в циклічний код Грея (у цьому коді позначаються клітини карти Карно). Таблиця істинності такого перетворювача наведена в табл. 3.5. Таблиця 3.5
За даними табл. 3.5 будуємо три карти Карно, щоб одержати три функції Y1=f1(Х2,Х1,Х0), Y2=f2(Х2,Х1,Х0), Y3=f3(Х2,Х1,Х0) (рис. 3.4).
Рис. 3.4. Карти Карно для вихідних функцій перетворювача кодів
Після мінімізації одержуємо такі функції:
Функціональна схема перетворювача наведена на рис. 3.6.
Рис. 3.6. Перетворювач двійкового кода в код Грея Завдання Дослідження шифраторів» ПОРЯДОК ВИКОНАННЯ РОБОТИ 1. Вивчити призначення, основи роботи та особливості застосування. Ознайомитися з основними принципами побудови схем шифраторів.
Таблиця 3.6
3. Використовуючи елементи стенду зберіть схему шифратора, отриману після перетворення КС, яка виконує рішення системи рівнянь, отриманої в завданні, в базис 2И-HE для трехразрядного чисел. Подайте на вхід необхідні сигнали і перевірте правильність функціонування зібраної схеми. Після закінчення досліджень оформити звіт. Дослідження дешифраторів» ПОРЯДОК ВИКОНАННЯ РОБОТИ 1. Вивчити призначення, основи роботи та особливості застосування. Ознайомитися з основними принципами побудови схем дешифраторів.
Таблиця 3.7
3. Використовуючи елементи стенду, зберіть схему трехвходового дешифратора, отриману після перетворення КС, яка виконує рішення системи рівнянь, отриманої в завданні, в базисі 2І-HE. Подайте на вхід необхідні сигнали і перевірте правильність функціонування зібраної схеми. Після закінчення досліджень оформити звіт.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.148.67 (0.009 с.) |

 ) і перетворює m -розрядний унітарний код в n -розрядний двійковий код.
) і перетворює m -розрядний унітарний код в n -розрядний двійковий код.

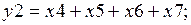



 ;...,
;...,  .
. ;
; ,
,
 01
01
 00
00
 0
0
 0
0
 1
1
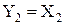 ;
;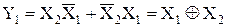 ;
; .
.



