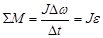Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение движения электроприводаСодержание книги
Поиск на нашем сайте
В механическом движении электропривода участвуют: · подвижная часть электродвигателя (ротор или якорь), · элементы механического передаточного устройства · исполнительный орган.
Совокупность этих элементов называют механической частью ЭП. Движение любого элемента механической части электропривода подчиняется законам механики. Поступательное движения при неизменной массе элементов движения описывается следующим уравнением:
где: m - масса элемента; t - время, v - линейная скорость движения элемента. a - ускорение поступательного движения элемента
Вращательное движения при неизменной массе элементов движения описывается следующим уравнением:
где: - J - момент инерции элемента; t - время, ω - угловая скорость движения элемента. ε - ускорение вращательного движения элемента
Данные уравнения можно записать иначе:
Уравнения отражают известный закон механики: ускорение движения механического элемента (тела) пропорционально алгебраической сумме действующих на него сил (моментов) и обратно пропорционально его массе (моменту инерции).
Если ∑F = 0; ∑M=0, то a =0; ε = 0 и элемент движется с постоянной скоростью или находится в состоянии покоя.
Элемент будет двигаться с неизменной скоростью (или будет неподвижным), если сумма сил или моментов, к нему приложенных, будет равна нулю. Такое движение называют установившимся.
При ∑F > 0 или ∑М > 0 элемент будет двигаться с ускорением, а при∑F < 0 или ∑М < 0 - с замедлением. Определение приведенного момента инерции J. Запишем выражения для определения кинетической энергии элементов в реальной (см. рис. 3.2 ) и расчетной (см. рис. 3.3) схемах и приравняем их друг к другу
где J1 - суммарный момент инерции элементов, вращающихся со скоростью ω (кроме двигателя), J2 - момент инерции элементов, вращающихся со скоростью барабана ωб .
Умножим обе части выражения на
Из технической механики известно, что: · отношение
· отношение
С учетом этого окончательно получаем:
Отсюда вытекает общее правило:
для расчета J следует моменты инерции вращающихся элементов разделить на квадрат передаточного числа кинематической схемы между этими элементами и валом двигателя, а массы поступательно движущихся элементов умножить на квадрат радиуса приведения и полученные результаты расчета сложить с моментами инерции двигателя и элементов, вращающихся с его скоростью.
Определение приведенного момента нагрузки Мс
При подъеме груза к исполнительному органу от электропривода должна быть подведена следующая механическая мощность
где:g - ускорение силы тяжести; FИО - усилие, развиваемое исполнительным органом.
Учитывая с помощью КПД потери мощности в кинематической цепи, запишем баланс мощности нагрузки ЭП в реальной и расчетной схемах:
где
Разделим обе части уравнения на ω, тогда:
Если исполнительный орган совершает не поступательное, а вращательное движение, то
где МИО - момент нагрузки ω ИО - скорость исполнительного органа,
Приведенный момент Мс иногда называют статическим или моментом сопротивления
В электроприводе двигатель создает движущий момент, а исполнительный орган – момент сопротивления движению. (М - Мс), тогда формула суммарного момента (см. занятие 2)
принимает вид
Левая часть уравнения, представляющая собой разность моментов двигателя и нагрузки и определяющая условия ускорения или замедления движения, в теории электропривода получила название динамического момента,
Мдин = М - Мс. При положительном динамическом моменте Мдин ˃0; М ˃Мс. скорость электропривода увеличивается При отрицательном динамическом моменте Мдин ˂0; М ˂Мс. скорость электропривода уменьшается
|
|||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 795; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.170.253 (0.007 с.) |


 - совокупность сил, действующих на элемент;
- совокупность сил, действующих на элемент;
 - совокупность моментов, действующих на элемент;
- совокупность моментов, действующих на элемент;


 , получим
, получим
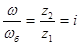 (z2 и z1, - соответственно число зубцов шестерен 6 и 5) является передаточным отношением редуктора,
(z2 и z1, - соответственно число зубцов шестерен 6 и 5) является передаточным отношением редуктора, представляет собой радиус приведения кинематической схемы между исполнительным органом (крюком 10) и валом двигателя.
представляет собой радиус приведения кинематической схемы между исполнительным органом (крюком 10) и валом двигателя.



 - результирующий КПД кинематической схемы ЭП;
- результирующий КПД кинематической схемы ЭП; и
и  — соответственно КПД редуктора 4 и барабана 8.
— соответственно КПД редуктора 4 и барабана 8.

 - приведенный момент нагрузки
- приведенный момент нагрузки