
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ального развития современного человека. Математические знанияСодержание книги
Поиск на нашем сайте
Необходимы для изучения явлений природы, без них невозможно Достижение успехов в развитии производства и науки. Знания о Количественных отношениях и пространственных формах окружа- Ющего мира необходимы практически во всех сферах деятельности Человека. Методы, применяемые в математике, необходимы для специалистов в любой сфере деятельности, особенно в сфере наукоемких технических производств. Вы сделали осознанный выбор изучения математики на повышенном уровне. А значит, вы уже осознанно нацелены на получение технической специальности в будущем. Поэтому на протяжении двух последующих учебных лет мы с вами будем работать на формирование у вас прочных математических знаний и умений, необходимых для продолжения образования в областях, требующих углубленной математической подготовки, развитие компетенций, востребованных в условиях непрерывного образования и будущей Профессиональной деятельности. Повторение теоретического материала, изученного по теме «Функция» в 9 классе Мы начинаем с вами новую очень важную в математике тему «Функции». Школьный курс алгебры построен таким образом, что с понятием функция приходится встречаться очень часто на протяжении нескольких лет обучения. При этом, названия функций перекликаются с видами соответствующих им уравнений и неравенств. К примеру, когда речь идет о линейных функциях, то говорят и о линейных уравнениях и неравенствах, то же самое касается квадратичных, показательных, логарифмических и прочих функций. Для удобства мы с вами выделим обсуждение понятия «функция» и основных свойств функций в отдельную тему. Так что же такое функция? Вспомним определение. Функция – это закон соответствия между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует только одно определенное значение другой величины y (функции или зависимой переменной). В указанном определении необходимо сразу обратить внимание на именно однозначное соответствие значений функции значениям аргумента. Под функцией можно понимать как соответствие определенных чисел, так и других объектов. Например, каждому значению времени в минутах соответствует строго одно значение времени в секундах, при этом, закон соответствия этих величин нам известен – количество минут необходимо умножить на 60 и получится количество секунд. Скажем, в 3 минутах 180 секунд, а в 5 минутах 300 секунд. При этом каждому значению количества секунд соответствует строго одно определенное количество минут. Т. е. и зависимость секунд от минут и обратная зависимость являются функциями. Это мы привели пример числовой функции. Примером нечисловой функции может быть однозначное соответствие человека и его фамилии. Обратите внимание, что у человека не может быть нескольких фамилий, но при этом есть однофамильцы, т. е. одной фамилии может соответствовать много разных человек, вспомните, например, сколько в России Ивановых. Это значит, что соответствие между человеком и фамилией однозначное, а обратное – нет. В первом случае соответствие будут называть функцией, а во втором нет. Но не следует думать, что из приведенных примеров следует, что все числовые зависимости являются функциями, а нечисловые необязательно. Примером числовой зависимости, которая не является функцией, может быть соответствие между числом, на которое указывает стрелка часов, и временем суток. Например, часовая стрелка указывает на восьмерку, а это может означать как 8-00 утра так и 20-00 вечера. Как же называть такие неоднозначные соответствия? Иногда их называют многозначными функциями, при этом, используя просто термин «функция» имеют в виду именно ее однозначность. В математике нас, конечно же, будут интересовать именно числовые функции. Их удобно описывать именно графическим способом. При этом, графическое изображение однозначной функции называют построением графика функции, а изображение многозначной функции – построением геометрического места точек или ГМТ. Давайте вспомним самые основные способы задания числовых функций: 1) Аналитический способ – задание функции с помощью формулы. С таким способом мы сталкиваемся наиболее часто. Обозначать в общем виде такую формулу принято обычно как
Что может означать указанная формула? Например, соответствие длины стены квадратной комнаты и ее площади. С помощью такой функции можно легко ответить, что такой комнате со стороной 4 метра соответствует одна единственная площадь Кстати, стоит обратить внимание, что обозначение аргумента и функции латинскими буквами нормальной будет запись функции в виде 2) Табличный способ – задание функции с помощью таблицы связанных друг с другом значений. Такой способ зачастую используется, если не известно правило соотношения между аргументом и функцией. Примером такого задания функции может послужить таблица средних температур за несколько дней мая:
3) Графический способ – задание функции с помощью изображения точек в системе координат, когда одной координате точек поставлена в однозначное соответствие другая ее координата. Например, в декартовой системе координат изображается множество точек, у которых поставлены в соответствие координаты по оси абсцисс (Ox) и координаты по оси ординат (Oy). Если привести в пример график все той же функции
Такой способ задания функции очень наглядный и позволяет быстро анализировать различные ее свойства, например, монотонность, четность, периодичность и т. п. О них мы скоро поговорим. Что касается различий в графических изображениях графиков функций и ГМТ многозначных функций, то существует быстрый способ их отличать друг от друга: любая вертикальная линия, проведенная в системе координат, пересекает график функции только в одной точке, а ГМТ многозначной функции в нескольких. Изобразим это на рисунке. График линейной функции – прямая или квадратичной – парабола:
ГМТ окружности или эллипса:
Область определения, область значений Теперь рассмотрим основные свойства и характеристики функций. И одной из важнейших характеристик функции является ее область определения. Область определения функции – это множество значений аргумента, для которых функция имеет смысл. Иными словами это допустимые значения икса. Это множество принято обозначать D или D(f). При решении уравнений вы привыкли называть такое множество аргументов, которые в них входили, областью допустимых значений (ОДЗ) или естественной областью определения (ЕОО). Для функций такой терминологией лучше не пользоваться, так как есть опасность перепутать область допустимых значений аргумента с областью значений функции из-за схожести названий. Искать область определения функции можно различными способами: Если функция задана аналитически, как это чаще всего бывает, то в таком случае удобнее всего сначала найти те значения аргумента, при которых функция не имеет смысла, и исключить их из множества действительных чисел. Например, для функции Перечислим основные случаи, в которых необходимо искать не имеющие смысла для функции аргументы: 1. Наличие в функции деления на выражение, содержащее неизвестную. В таком случае исключаются те аргументы, при которых возникает деление на ноль. Например, в функции 2. Присутствие в функции корня четной степени из выражения, содержащего неизвестную. При этом необходимо исключить аргументы, при которых подкоренное выражение отрицательно, в таком случае удобно сразу накладывать условие, что подкоренное выражение больше или равно нулю. Например, для функции Обратите внимание, что для корней нечетной степени, например, кубических такого ограничения нет. Конечно же, функции могут содержать и композиции из указанных выражений, например, деление на выражение, содержащее арифметический квадратный корень. В таком случае для нахождения области определения записывается система из указанных ограничений. Кроме того, мы указали не все возможные ситуации, при которых необходимо искать ограничения на область определения. Например, тангенс имеет смысл не при всех значениях аргумента. Функции, в которых нет действий, ограничивающих множество аргументов, областью определения является все множество действительных чисел. Это относится, например, к линейным и квадратичным функциям. Так для функции 2) Для функций, заданных табличным способом, область определения явно указана в таблице – это все множество перечисленных аргументов. Например, для функции, которая задана таблицей:
Областью определения будет 3) Если функция задана графически, т. е. изображен ее график, то областью определения будет множество значений координат точек графика по оси абсцисс. Иными словами необходимо искать все значения иксов, для которых изображены точки графика. Например, для графика функции
Областью определения будет
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.130.151 (0.011 с.) |

 , где под
, где под  понимают аргумент, а под
понимают аргумент, а под  значение функции. При этом, свободно используются, например, такие равноправные записи:
значение функции. При этом, свободно используются, например, такие равноправные записи:
 .
. (от слова «function»). Вполне
(от слова «function»). Вполне . Подумайте сами, какой буквой здесь что обозначено.
. Подумайте сами, какой буквой здесь что обозначено.
 , то он будет иметь вид не безызвестной вам параболы:
, то он будет иметь вид не безызвестной вам параболы: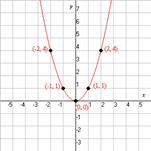











 областью определения является
областью определения является  , т. к. она определена при всех значениях икса, кроме нуля, поскольку на ноль делить нельзя.
, т. к. она определена при всех значениях икса, кроме нуля, поскольку на ноль делить нельзя.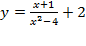 из области определения необходимо исключить аргументы, при которых
из области определения необходимо исключить аргументы, при которых  , или сразу же наложить ограничение
, или сразу же наложить ограничение 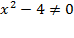 .
.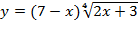 областью определения будет решение неравенства
областью определения будет решение неравенства  .
. областью определения будет
областью определения будет  .
.



 . Как видите, в случае табличного задания функции множество допустимых значений аргументов не является непрерывным и не может быть задано в виде промежутка, так как это определенный набор конкретных данных.
. Как видите, в случае табличного задания функции множество допустимых значений аргументов не является непрерывным и не может быть задано в виде промежутка, так как это определенный набор конкретных данных.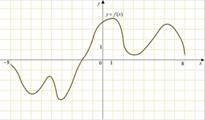
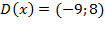 . Края отрезка не включены, т. к. на графике крайние точки выколоты.
. Края отрезка не включены, т. к. на графике крайние точки выколоты.


