Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятностей для схемы бернулли
Хотя формула Бернулли и является точной, она не всегда удобна. Например, при 100 бросках монеты
и вычисление точного ответа затруднительно. Формула Бернулли приемлема для вычислений, если число испытаний не превышает 10-15. При больших n используют либо формулу Лапласа, либо формулу Пуассона. Формула Лапласа (локальная теорема Лапласа)
тем точнее, чем больше n. Здесь n, k, p, q - те же величины, что и в формуле Бернулли. Функция j(x) четная: j(-x) = j(x). Она быстро убывает: считают, что при x > 4 j(x) = 0. Таблица, позволяющая вычислять значения функции j(x), имеется во всех учебниках и задачниках по теории вероятностей. Впрочем, можно не иметь таблицы, а иметь калькулятор, вычисляющий экспоненту (функцию ех).
Пример 1. Вероятность выпадения ровно 50 “орлов” при 100 бросках монеты Р100(50) вычислим по формуле Лапласа. Здесь n = 100,k = 50,p=0,5, q = 0,5, k - np = 0,
Пример 2. Найти вероятность выпадения от 47 до 57 “орлов” при 100 бросках монеты. При решении подобных задач (при n > 15) используют интегральную теорему Лапласа: вероятность Рn(k1,k2) появления события в n испытаниях от k1 до k2 раз Здесь n, p, q те же, что и в примере 1: n=100, p = q =0,5, k1=47, k2 = 57.
Функция F вычисляется с помощью таблиц (см. приложение).
Функция Ф(x) нечетная: Ф(-х) = - Ф(х). При х > 5 считают, что Ф(х) = 0,5. Итак, Р100(47,57) = Ф(1,4) + Ф(0,6). По таблице Ф(1,4) = 0,4192, Ф(0,6) = 0,2257, поэтому Р100(47,57) = 0,6449. При небольших значениях вероятности p (меньших 0,1) и больших значениях n более точный результат дает другая приближенная формула - формула Пуассона l называется параметром распределения Пуассона, а сама формула выражает “закон редких явлений” (т. к. p мало). Пример 3. Первый черновой набор “Методических указаний” на 50 страницах содержит 100 опечаток. Какое из событий вероятнее: на наудачу взятой странице нет опечаток, 1 опечатка, 2 опечатки, 3 опечатки? Вероятность того, что данная опечатка попадет на наудачу взятую страницу равна 1/50 = 0,02, число испытаний (опечаток) n = 100. Поскольку p мало, воспользуемся формулой Пуассона с параметром l = np = 2. Вероятность того, что опечаток нет Другие вероятности
Как видим, наибольший коэффициент при е-2 у Р100(1) и Р100(2). Ответ: наиболее вероятны 1 или 2 опечатки, их вероятность КОММЕНТАРИИ К ЗАДАЧЕ №3
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ДИСКРЕТНОГО ТИПА.
Cлучайной величиной называют величину, которая в результате испытания примет одно и только одно возможное числовое значение из заранее известной совокупности значений. Случайной величиной дискретного типа (дискретной случайной величиной) называется величина, которая может принимать либо конечное число возможных значений, либо такое бесконечное число значений, которые могут быть расположены в числовую последовательность Е1, Е2,.... Для каждого из этих значений указывают его вероятность. Сумма этих вероятностей должна быть равна 1. Если случайная величина принимает только одно значение, то соответствующая ему вероятность равна 1.
Пример 1. Пусть Х1 - число “орлов”, выпавших при двух бросках симметричной монеты. Х может принимать значения 0, 1 или 2 с вероятностями, вычисленными по формуле Бернулли: Дискретные случайные величины записывают в виде таблицы. Для данного примера получим:
Верхняя строчка возможные значения Х1, Р их вероятности, сумма которых равна 1. С помощью таблицы можно считать вероятности попадания случайной величины дискретного типа в интервалы. Например, для заданной выше случайной величины Х
Пример 2. В полном наборе игры в домино 28 костей. Пусть Х2 – сумма очков на случайно выбранной кости. Поскольку наименьшее значение такой суммы равно 0 («пусто-пусто»), следующее – 1 и так до 12 («6-6»), Х является случайной величиной дискретного типа. Зададим ее таблицей.
Вероятности в этой таблице вычислены по формуле классической вероятности, в числителях дробей количества костей домино с данным числом очков, знаменатели равны общему числу костей. Случайные величины традиционно обозначаются заглавными буквами X, Y, Z,..., а их возможные значения - прописными: x1, x2, y1, и т. д. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ.
Если F(x) = P(X < x), то функция F(x) называется функцией распределения (интегральной функцией распределения) случайной величины Х, т.е. функция распределения в точке “х” - это вероятность того, что случайная величина Х примет значение, меньшее заданного числа х.
Из определения сразу следуют несколько свойств F(x): F(- ¥) = 0, F(+ ¥) = 1; F(x) - неубывающая функция (т.е. если x1 < x2 , то F(x1) £ F(x2)). Функция распределения для случайной величины дискретного типа имеет “ступенчатый” график. Для случайной величины Х1 из §13 F(x) запишется так:
Обратите внимание, что левые концы «ступенек» - выколотые, а правые - нет. Например, F(1) = P(X1 < 1) = P(X1 =0) = 0,25; F(1,1) = P(X1<1,1) = P(X1 = 0) + P(X1 = 1) = 0,75. «Высоты» «ступенек» равны очередным вероятностям, взятым из таблицы: сначала 0,25, затем еще +0,5, и наконец еще +0,25. Аналогичный график и для другого примера – про домино – только там будет не 2, а 12 «ступенек». Справедлива формула: P(a £ X < b) = F(b) - F(a).
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 450; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.127 (0.011 с.) |
 ,
, ,
,  ,
, 
 и
и  .
.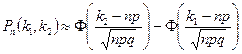


 , l = np
, l = np (т.к. 0! = 1)
(т.к. 0! = 1) ,
,  ,
,  .
. .
. . Т. к. p = q = 0,5, то эти вероятности равны 0,25; 0,5; 0,25 соответственно.
. Т. к. p = q = 0,5, то эти вероятности равны 0,25; 0,5; 0,25 соответственно. .
.