
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2.2. Нормальное распределениеСодержание книги
Поиск на нашем сайте
Тестовые задания закрытого типа (Задания множественного выбора)
********************************************************************************** Т41. (выберите один вариант ответа) Распределение значений признака, часто встречаемое в самых различных областях науки и практики, первоначально принималось за норму всякого массового случайного проявления признаков и в соответствии с этим получило свое название – это Варианты ответа: 1) нормальное распределение; (В) 2) монограмма; 3) номограмма; 4) случайное распределение. ********************************************************************************** Т42. (выберите один вариант ответа) Закон нормального распределения выражается формулой. 1) 2) 3) 4) где: p – теоретическая частота каждого класса распределения; n – объем группы, число объектов исследования; k – классовый промежуток, (величина классов); ********************************************************************************** Т43. (выберите один вариант ответа) В любом нормальном распределении доля объектов со значением признака, отличающимся от средней арифметической не более чем на 2 σ (σ – среднее квадратичное отклонение), % равна: Варианты ответа: 1) 98,75; 2) 99,73; 3) 85,75; 4) 95,45. (В) ********************************************************************************** Т44. (выберите один вариант ответа) В любом нормальном распределении доля объектов со значением признака, отличающимся от средней арифметической не более чем на 3 σ (σ – среднее квадратичное отклонение), % равна: Варианты ответа: 1) 98,75; 2) 99,73; (В) 3) 85,75; 4) 95,45. ********************************************************************************** Т45. (выберите один вариант ответа) В любом нормальном распределении доля объектов со значением признака, отличающимся от средней арифметической не более чем на 2,5 σ (σ – среднее квадратичное отклонение), % равна: Варианты ответа: 1) 98,75; (В) 2) 99,73; 3) 85,75; 4) 95,45. ********************************************************************************** Т46. (выберите один вариант ответа) Выборочный коэффициент, определяемый по формуле:
где M3– центральный выборочный момент третьего порядка,
mi – частота. Варианты ответа: 1) коэффициент асимметрии; (В) 2) эксцесс; 3) коэффициент корреляции; 4) коэффициент крутости. ********************************************************************************** Т47. (выберите один вариант ответа) Форма полигона, когда одна из ветвей его, начиная с вершины имеет более пологий «спуск», чем другая: Варианты ответа: 1) асимметричная; (В) 2) симметричная; 3) астигматичная; 4) симпатичная. ********************************************************************************** Т48. (выберите один вариант ответа) Выборочный коэффициент крутости, определяемый формулой где M4 – центральный выборочный момент четвертого порядка;
Варианты ответа: 1) коэффициент асимметрии; 2) коэффициент корреляции; 3) регресс; 4) эксцесс. (В) ********************************************************************************** Т49. (выберите один вариант ответа) Выборочный коэффициент, служащий для сравнения на «крутость» выборочного распределения – это:
Варианты ответа: 1) коэффициент асимметрии; 2) коэффициент корреляции; 3) коэффициент усиления; 4) эксцесс. (В) ********************************************************************************** Т50. (выберите один вариант ответа) Эксцесс для случайной величины, распределенной нормально, равен……. Варианты ответа: 1) коэффициенту асимметрии; 2) единице; 3) средней арифметической; 4) нулю. (В) ********************************************************************************** Т51. (выберите один вариант ответа) Коэффициент, принимающий положительное значение, в случае, когда полигон более крутой по сравнению с нормальной кривой – это коэффициент: Варианты ответа: 1) асимметрии; 2) корреляции; 3) усиления; 4) эксцесса. (В) ********************************************************************************** Т52. (выберите один вариант ответа) Коэффициент, принимающий отрицательное значение, в случае, когда полигон имеет более пологую вершину по сравнению с нормальной кривой – это коэффициент: Варианты ответа: 1) эксцесса; (В) 2) корреляции; 3) усиления; 4) асимметрии. ********************************************************************************** Т141 Тест на соответствие Поставьте в соответствие номеру определения (формулы) в таблицы 1 номер термина из таблицы 2 Таблица1
Таблица 2
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.006 с.) |

 ; (В)
; (В) ;
; ;
; ;
; – отношение окружности к диаметру равно 3,1416; e – основание натуральных логарифмов равно 2,71828;
– отношение окружности к диаметру равно 3,1416; e – основание натуральных логарифмов равно 2,71828; 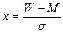 – нормированное отклонение средин каждого класса распределения; σ – среднее квадратичное отклонение; m – ошибка опыта; М – среднее арифметическое.
– нормированное отклонение средин каждого класса распределения; σ – среднее квадратичное отклонение; m – ошибка опыта; М – среднее арифметическое. ,
, – среднеквадратическое отклонение,
– среднеквадратическое отклонение, – среднее арифметическое,
– среднее арифметическое, ,
, ,
,
 – среднее арифметическое,
fi – частота,
– среднее арифметическое,
fi – частота,
 ,
,
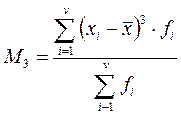 ,
,
 ,
,



