
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Датчики угла и рассогласованияСодержание книги Поиск на нашем сайте
Под термином «датчики угла» понимаются устройства, преобразующие угловую координату в электрическое напряжение. Это напряжение используется в системах автоматики как сигнал обратной связи по углу или как управляющий сигнал в задающих устройствах. Датчики угла, например, находят применение в следящих системах для измерения угла поворота исполнительного вала. Задание на движение системы может выполняться также с помощью датчика угла, угловой координатой которого является угол поворота командной (задающей) оси. Разность сигналов этих двух датчиков, так называемое «рассогласование», подается как управляющий сигнал на вход системы. В этом случае оба датчика могут рассматриваться объединенно как «датчик рассогласования». Для датчиков угла и рассогласования широкое применение нашли сельсины.
В схемах датчиков угла входная координата сельсина - угол поворота его ротора θ, а выходные координаты - амплитуда Uвыхm и фаза j выходного напряжения по отношению к переменному опорному напряжению (рис. 5.1, а). В зависимости от использования той или другой выходной координаты различают амплитудный режим, когда j = const (0 или p), а Uвыхm = = f(θ), и режим фазовращателя, когда Uвыхm = const, a j = f(θ). В амплитудном режиме обмотка возбуждения получает питание от сети переменного тока (рис. 5.1, б):
Uв = Uвmsinwt. (5.1) Магнитный поток, действующий по осевой линии обмотки возбуждения, наводит соответствующие ЭДС в фазах обмотки статора. Пренебрегая потоком рассеяния и активным сопротивлением обмотки возбуждения, с учетом (5.1), имеем для фазных ЭДС следующие выражения:
где Здесь за начало отсчета угла поворота ротора θ принята осевая линия обмотки фазы А статора. Линейная ЭДС определится разностью соответствующих фазных ЭДС и с учетом (5.2):
Если начало отсчета угла переместить на p / 3 в направлении к фазе В, то относительно угла θ' = p / 3 - θ в новой системе отсчета с учетом (5.3)
Характеристика управления сельсина в амплитудном режиме приобретает синусоидальную закономерность и с учетом (5.4):
где Eлm - амплитуда линейной ЭДС статора. Значения Eлm принято считать условно положительными при j = 0, а условно отрицательными при j = p. Для малых θ', когда
где
В режиме фазовращателя обмотка статора получает питание от источника трехфазного напряжения с неизменной амплитудой. Образующееся круговое вращающееся поле в любой фиксированной точке статора, удаленной от оси отсчета (оси фазы А) на угол j характеризуется магнитным потоком
Ф = Фmcos(wt - j). Следовательно, в обмотке ротора, ось которой сдвинута на угол j = θ относительно начала отсчета, наводится ЭДС
где E1m - амплитуда фазной ЭДС статора. Коэффициент 3/2 в последней формуле учитывает увеличение амплитуды вектора магнитной индукции кругового вращающегося поля по отношению к амплитуде вектора пульсирующего магнитного поля, создаваемого фазной обмоткой статора. Таким образом, характеристика управления сельсина в режиме фазовращателя определяется равенством j = θ.
где
Для малых углов рассогласования
где Для большинства сельсинных пар в схеме датчика рассогласования
В связи с нелинейностью характеристики управления (5.5) практически диапазон измерения углов сельсинными датчиками составляет
Для измерения малых углов с хорошей точностью используются повышающие измерительные редукторы, увеличивающие крутизну характеристики управления сельсина в iр раз. При этом к точности изготовления редуктора предъявляются повышенные требования. В первую очередь применяются конструкции редукторов, практически исключающие люфты в кинематических парах. При скорости вращения вала, ограниченной допустимой динамической погрешностью измерения угла, сельсин в динамике может рассматриваться как безынерционное звено. Для измерения углов в больших диапазонах и с высокой точностью используются дискретные датчики. Их функциональной выходной величиной является число, представленное в двоичной системе счисления с помощью электрических дискретных сигналов. Необходимая точность достигается соответствующим числом разрядов датчика. Простейший цифровой датчик угла,контактный с кодовым диском, рассмотрен в /1/. Его устройство поясняется рис. 5.4. Диск жестко соединен с валом, угол поворота которого подлежит преобразованию в цифровой код. Кодовый рисунок диска состоит из концентрических колец (дорожек), каждое из которых имеет чередующиеся электрически проводящие и непроводящие участки. Кольцо с наименьшим радиусом, имеющее два участка, относится к старшему разряду выходного числа, а кольцо с наибольшим радиусом - к младшему разряду. В каждом последующем от центра кольце число участков удваивается, что соответствует в двоичном коде переходу от одного разряда к другому. К токопроводящим участкам (заштрихованным на рис. 5.4, а) подводится напряжение через внешнее кольцо. Считывание осуществляется с помощью
Δθ0 = 360 о / 2n датчик не реагирует на изменение входной величины и его характеристика управления приобретает ступенчатый вид (рис. 5.5, б). Погрешность, вызванная дискретностью,
тем меньше, чем больше число разрядов в датчике. Так как на одном кодовом диске трудно реализовать число разрядов более трех-четырех, то для повышения точности датчика применяют несколько кодовых дисков, соединенных с входным валом через редуктор и поворачивающихся с различными скоростями. Самые старшие разряды выходных цифровых данных снимаются с самого медленного диска, а самые младшие разряды - с самого быстрого диска. Контактная система и погрешности измерительных редукторов лимитируют точностные показатели датчика. Практически реализуемое число разрядов в цифровом датчике угла данного типа не превосходит 9 - 10, что соответствует интервалу дискретности 21'- 42'.Поэтому в высокоточных системах с допустимыми погрешностями менее 1' контактный датчик применяется для грубого отсчета угла.
Вопросы для самопроверки
1. Что является входной и выходной координатами датчика угла поворота? 2. Что является входной и выходной координатами датчика угла рассогласования? 3. В каких системах могут применяться датчики угла и датчики рассогласования? 4. Сколько обмоток и где имеет трехфазный контактный сельсин? 5. Что является входной и выходными координатами сельсина? 6. В каких режимах может работать сельсин? 7. Что такое амплитудный режим работы сельсина? 8. Что такое фазовый режим работы сельсина? 9. Приведите формулу для расчета характеристики управления сельсина в амплитудном режиме работы. 10. Приведите формулу для расчета характеристики управления сельсина в фазовом режиме работы. 11. Какими факторами определяются статические погрешности сельсина, искажающие его характеристику управления? 12. Чем вызвана скоростная погрешность датчика угла поворота на основе сельсина? 13. В каком режиме работают сельсин-датчик и сельсин-приемник в схеме датчика угла рассогласования, если в качестве его выходных координат используются амплитудное значение ЭДС ротора сельсина-приемника и фаза этой ЭДС? 14. Приведите формулу для расчета характеристики управления датчика рассогласования на основе двух сельсинов, работающих в трансформаторном режиме.
15. Что является основными недостатками датчиков угла поворота на основе сельсина? 16. С какой целью на входе датчиков угла поворота используются понижающие измерительные редукторы? 17. С какой целью на входе датчиков угла поворота используются повышающие измерительные редукторы? 18. Как изменяется погрешность измерения угла при использовании понижающих измерительных редукторов? 19. Когда целесообразно использование дискретных датчиков угла? 20. Какие основные элементы присутствуют в конструкции цифрового датчика угла поворота на основе кодового диска? 21. Почему характеристика управления цифрового датчика угла поворота на основе кодового диска имеет ступенчатый характер? 22. Приведите формулу для расчета интервала дискретности цифрового датчика угла поворота на основе кодового диска. 23. Приведите формулу для расчета абсолютной погрешности цифрового датчика угла поворота на основе кодового диска. 24. Путем каких конструкционных мер можно увеличить разрядность цифрового датчика угла поворота на основе кодового диска? Датчики угловой скорости Тахогенератор постоянного тока представляет собой электрическую машину постоянного тока с независимым возбуждением или постоянными магнитами (рис. 5.6). Входная координата ТГ- угловая скорость w, выходная - напряжение Uвых, выделяемое на сопротивлении нагрузки. Так как Eтг = kФw = I(Rтг+Rн), то где
Передаточный коэффициент ТГ, строго говоря, не остается постоянным при изменении скорости из-за нелинейности сопротивления щеточного контакта и реакции якоря. Поэтому в характеристике управления наблюдается определенная нелинейность в зонах малой и большой скоростей (рис. 5.6, б). Нелинейность в зоне малой скорости уменьшают применением металлизированных щеток с малым падением напряжения. Нелинейность характеристики из-за реакции якоря снижается ограничением сверху скорости и увеличением сопротивления нагрузки. При выполнении указанных мероприятий характеристику управления ТГ можно считать практически прямолинейной. На работу ТГ существенное влияние оказывают конструктивно-технологические погрешности. Это коллекторные пульсации напряжения, обусловленные конечным числом коллекторных пластин, пульсации из-за зубцовой конструкции якоря, оборотные пульсации, вызванные несимметрией воздушного зазора. Погрешности от указанных пульсаций сильнее искажают выходной сигнал ТГ в области низких скоростей. При снижении скорости уменьшается их частота и увеличивается амплитуда относительно уровня передаваемого сигнала. Эти погрешности ограничивают нижний предел скорости ТГ. Для уменьшения перечисленных пульсаций тахогенераторы выполняются с повышенным числом коллекторных пластин, со скошенными по винтовой линии на одно зубцовое деление пазами якоря, с увеличенным воздушным зазором. Тахогенераторы высокой точности выполняются с полым беспазным якорем. Для дополнительного снижения пульсации к выходу ТГ подключают конденсатор (рис. 5.6, а), при этом передаточная функция ТГ приобретает вид
где
Тахогенераторы переменного тока (рис.5.7) наиболее часто выполнены на базе асинхронной двухфазной машины. На статоре имеются две взаимно перпендикулярные обмотки: обмотка возбуждения, расположенная по оси a, и выходная управляющая обмотка, расположенная по оси b, включенная на сопротивление нагрузки тахогенератора Zтг. Для уменьшения момента инерции ротор выполняется тонкостенным в виде полого стакана из немагнитного материала (обычно алюминиевого сплава). Внутри ротора размещается неподвижный стальной шихтованный сердечник, по которому замыкается магнитный поток. Соотношения для расчета регулировочной характеристики тахогенератора приведены в /1/. Сопротивление нагрузки тахогенератора существенно влияет на амплитуду и фазу выходного напряжения. Потому для снижения амплитудных и фазовых искажений выходного напряжения необходимо использовать тахогенератор в режиме, близком к холостому ходу, то есть соединять тахогенератор с нагрузкой через эмиттерный повторитель, имеющий большое входное сопротивление. Если ТГ работает в режиме холостого хода, при котором
где
где Ua - модуль вектора напряжения возбуждения; Kтг - модуль комплексного коэффициента передачи; jвых - фаза вектора выходной ЭДС; a = R'р / xm - отношение приведенного к обмотке статора активного сопротивления ротора к индуктивному сопротивлению намагничивания; wс - синхронная скорость ротора; j - мнимая единица. Характеристики управления, соответствующие этому случаю приведены на рис. 5.8 тонкими линиями. Погрешности амплитуды ΔEвых m и фазы Δj могут быть существенно уменьшены ограничением диапазона измерения скоростей сверху. При смене знака угловой скорости ротора фаза jвых выходной ЭДС Eвых изменяется на 180о. При использовании асинхронного ТГ в обычных системах автоматического регулирования его выходную ЭДС подают на вход фазового детектора, работающего в амплитудном режиме, и с выхода фазового детектора снимают постоянное напряжение, величина которого будет прямо пропорциональна значению скорости ротора тахогенератора, а знак будет определяться направлением вращения ротора. Технологические неточности изготовления ТГ приводят к определенной магнитной и электрической асимметрии статора и ротора. Это приводит к появлению остаточной ЭДС, вызывающей погрешность ТГ в зоне малых скоростей. Если указанная погрешность выходит за рамки требуемой точности ТГ, то принимают определенные меры по ее компенсации. В частности, когда остаточная ЭДС характеризуется постоянством амплитуды и фазы, последовательно в цепь выходной обмотки ТГ вводится с помощью корректирующего устройства дополнительная ЭДС, равная остаточной ЭДС по амплитуде и противоположная ей по фазе.
В современных системах автоматики с большими диапазонами регулирования скорости и высокими требованиями к ее стабилизации точность ТГ может оказаться недостаточной. Для таких систем используются цифровые датчики скорости (ЦДС). Такие датчики рассмотрены в /1, 7/. Функционально в ЦДС можно выделить две основные части: импульсный преобразователь скорости - датчик импульсов (ДИ), преобразующий угловую скорость вала в импульсы с частотой f, пропорциональной скорости, и кодовый преобразователь - счетчик импульсов (СИ), формирующий на интервале измерения Т цифровой код An выходной величины датчика скорости (рис. 5.9).
где Nди - импульсная емкость кодового диска - число импульсов на один оборот диска.
Выделение импульсов на каналах положительной скорости (направление «вперед», UвыхВ) или отрицательной скорости (направление «назад», UвыхН) осуществляется логической схемой, одно из возможных исполнений которой приведено на рис. 5.13. На первом выходном канале импульсы UвыхВ появляются при таком направлении вращения, при котором сигнал U2 опережает по фазе на p /2 сигнал U1, и элемент совпадения И открыт для импульсов Uвых1. При другом направлении вращения, когда U2 отстает по фазе на p /2 от U1, элемент совпадения И открыт для импульсов Uвых2, которые поступают на второй выходной канал UвыхН.
Так как младшему разряду датчика соответствует один импульс, то разрешающая способность ЦДС составляет N: 1, а точность измерения d =1/N. Очевидно, дискретность по скорости датчика, об/с, определится величиной Δno = 1/(NдиT). Таким образом, точность ЦДС тем выше, чем больше измеряемая скорость и период измерения.
Второй способ формирования цифрового кода скорости состоит в определении интервала времени между двумя импульсами путем подсчета числа высокочастотных опорных импульсов, умещающихся на измеряемом интервале. Данный способ имеет, напротив, максимальную разрешающую способность на самых низких скоростях, когда период следования импульсов максимален и содержит наибольшее число опорных импульсов. Однако высокая точность датчика при низких скоростях относится также лишь к среднему за измеряемый интервал значению скорости. При повышении скорости точность данного ЦДС снижается. Рассмотренные варианты ЦДС обеспечивают высокую точность измерения скорости, и тем большую, чем продолжительней период измерения. Однако данный период измерения вносит в систему автоматики с ЦДС дискретность по времени, которая вносит искажения в работу высокодинамичных систем. Поэтому для снижения дискретности по времени в быстродействующих системах с управлением по интегралу сигнала рассогласования интегрирование разности скоростей выполняется подсчетом разности непосредственно числа импульсов с задающего устройства и с датчика импульсов с помощью реверсивного счетчика.
Вопросы для самопроверки 1. Для чего используются датчики скорости в системах автоматики? 2. Какой электрической машиной является тахогенератор постоянного тока? 3. Что является входной и выходной координатами тахогенератора постоянного тока? 4. Запишите формулу расчета характеристики управления тахогенератора постоянного тока. 5. Запишите формулу для расчета коэффициента передачи тахогенератора постоянного тока, нагруженного на активное сопротивление. 6. Какие параметры тахогенератора постоянного тока наиболее существенно снижают линейность его характеристики управления? 7. Какие мероприятия способствуют улучшению линейности характеристики управления тахогенератора постоянного тока в зоне малых скоростей? 8. Какие мероприятия способствуют улучшению линейности характеристики управления тахогенератора постоянного тока в зоне больших скоростей? 9. Какие особенности конструкции тахогенератора постоянного тока определяют наличие пульсаций в его выходном напряжении? 10. Какие особенности конструкции тахогенератора постоянного тока снижают уровень пульсаций его выходного напряжения? 11. С какой целью параллельно нагрузке тахогенератора постоянного тока включают конденсатор? 12. Приведите формулу для расчета передаточной функции тахогенератора постоянного тока с апериодическим фильтром на выходе, сглаживающим пульсации выходного напряжения. 13. Приведите формулу для расчета постоянной времени конденсаторного апериодического фильтра, включенного на выход тахогенератора постоянного тока. 14. Как сказывается на быстродействии тахогенератора постоянного тока наличие апериодического фильтра на его выходе? 15. На основе какой электрической машины наиболее часто выполняются тахогенераторы переменного тока? 16. Какая особенность конструкции асинхронного тахогенератора позволяет уменьшить момент инерции его ротора? 17. Какие обмотки имеет двухфазный асинхронный тахогенератор? 18. Что является входной координатой асинхронного тахогенератора? 19. Что является выходными координатами асинхронного тахогенератора? 20. С какой целью асинхронные тахогенераторы используются в режиме работы близком к холостому ходу? 21. Приведите формулу для расчета в комплексном виде характеристики управления асинхронного тахогенератора. 22. При каких допущениях модуль комплексного коэффициента передачи и фаза выходной ЭДС асинхронного тахогенератора будут постоянны? 23. Как изменяется фаза выходной ЭДС асинхронного тахогенератора при изменении направления вращения его вала? 24. Как изменяется модуль коэффициента передачи асинхронного тахогенератора при увеличении напряжения на обмотке возбуждения? 25. С какой целью выходное напряжение асинхронного тахогенератора может подаваться в систему регулирования через фазовый детектор, работающий в амплитудном режиме? 26. Каким параметром питающей сети ограничена полоса пропускания асинхронного тахогенератора? 27. Какие основные достоинства асинхронных тахогенераторов? 28. Какие основные недостатки асинхронных тахогенераторов? 29. В чем основные достоинства цифровых датчиков скорости? 30. Из каких основных узлов состоит структурная схема цифрового датчика скорости? 31. Что является входной и выходной координатами цифрового датчика ско-рости? 32. С какой целью на кодовом диске фотоэлектрического датчика импульсов предусмотрены две дорожки пропускающих свет щелей? 33. Что такое импульсная емкость кодового диска датчика импульсов? 34. Приведите формулу для расчета частоты выходных импульсов, формируемых датчиком импульсов на основе фотоэлектрического кодового диска? 35. Какие существуют способы формирования выходного цифрового кода датчика скорости на основе кодового диска? 36. Приведите формулу, связывающую на фиксированном временном периоде измерения среднее значение скорости вращения кодового диска датчика импульсов с числом генерируемых им импульсов. 37. Чему равна разрешающая способность цифрового датчика скорости, если его цифровой выходной код формируется путем подсчета числа импульсов импульсного датчика на фиксированном временном периоде измерения? 38. Чему равна дискретность по скорости (в оборотах в секунду) цифрового датчика скорости, если его цифровой выходной код формируется путем подсчета числа импульсов импульсного датчика на фиксированном временном периоде измерения? 39. Чему равна точность измерения цифрового датчика скорости, если его цифровой выходной код формируется путем подсчета числа импульсов импульсного датчика на фиксированном временном периоде измерения? 40. Как с увеличением измеряемой скорости и временного периода измерения изменяется точность цифрового датчика скорости, если его цифровой выходной код формируется путем подсчета числа импульсов импульсного датчика на этом временном периоде измерения? 41. Почему при формировании выходного кода цифрового датчика скорости нежелательно увеличение временного периода, на котором подсчитываются выходные импульсы импульсного датчика? 42. Как с увеличением измеряемой скорости изменяется точность цифрового датчика скорости, если его цифровой выходной код формируется путем подсчета числа опорных импульсов за промежуток времени между двумя следующими друг за другом импульсами импульсного датчика? 43. В чем основной недостаток цифровых датчиков скорости, формирующих выходной цифровой код путем подсчета числа импульсов импульсного датчика за фиксированный временной период измерения или путем подсчета числа опорных импульсов за промежуток времени между соседними выходными импульсами импульсного датчика? 44. В каких системах автоматики наиболее целесообразно использование цифровых датчиков скорости?
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 928; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.253.53 (0.017 с.) |

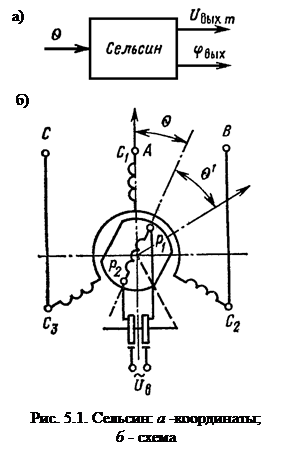 Сельсин - небольшая электрическая машина переменного тока, имеющая две обмотки: однофазную (обмотку возбуждения) и трехфазную (обмотку синхронизации). По конструктивному признаку сельсины разделяются на два основных типа: контактные сельсины и бесконтактные сельсины. Основное исполнение первого типа - обмотка возбуждения расположена на роторе, обмотка синхронизации - на статоре. Этим уменьшается до двух число контактных колец и исключаются контакты на синхронизирующей связи. Идея бесконтактного сельсина реализуется двумя способами. При первом способе благодаря специальной конструкции магнитопровода ротора неподвижная кольцевая обмотка возбуждения создает в роторе поток, поворачивающийся вместе с ротором. При втором способе обмотка ротора получает питание от вращающейся совместно с ротором вторичной обмотки кольцевого трансформатора возбуждения с неподвижной первичной обмоткой.
Сельсин - небольшая электрическая машина переменного тока, имеющая две обмотки: однофазную (обмотку возбуждения) и трехфазную (обмотку синхронизации). По конструктивному признаку сельсины разделяются на два основных типа: контактные сельсины и бесконтактные сельсины. Основное исполнение первого типа - обмотка возбуждения расположена на роторе, обмотка синхронизации - на статоре. Этим уменьшается до двух число контактных колец и исключаются контакты на синхронизирующей связи. Идея бесконтактного сельсина реализуется двумя способами. При первом способе благодаря специальной конструкции магнитопровода ротора неподвижная кольцевая обмотка возбуждения создает в роторе поток, поворачивающийся вместе с ротором. При втором способе обмотка ротора получает питание от вращающейся совместно с ротором вторичной обмотки кольцевого трансформатора возбуждения с неподвижной первичной обмоткой. ;
; ; (5.2)
; (5.2) ,
, - коэффициент трансформации между фазной статорной и роторной обмотками при их соосном положении.
- коэффициент трансформации между фазной статорной и роторной обмотками при их соосном положении. . (5.3)
. (5.3)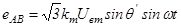 . (5.4)
. (5.4) , (5.5)
, (5.5) ,
,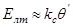 ,
, - передаточный коэффициент сельсина в амплитудном режиме.
- передаточный коэффициент сельсина в амплитудном режиме.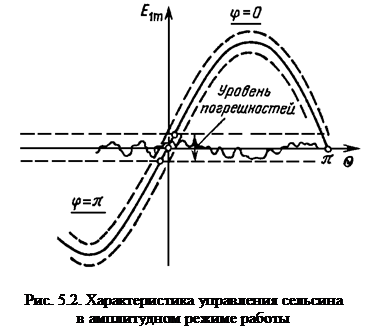 Характеристика управления сельсина в амплитудном режиме работы, построенная по (5.5), приведена на рис. 5.2. Полученные выражения для характеристики управления и передаточного коэффициента не учитывают погрешностей, вносимых в передачу сигнала сельсином несинусоидальностью распределения магнитной индукции, асимметрией магнитопровода, неравенством параметров фаз статорной обмотки и тому подобное. Перечисленные факторы обусловливают статические погрешности, искажающие форму характеристики управления. Эти погрешности в зависимости от класса точности изготовления сельсина характеризуются определенным уровнем (пунктирные линии на рис. 5.2). Наибольшее влияние они оказывают в области малых углов, где полезный сигнал соизмерим с погрешностями. Кроме статических погрешностей при вращении сельсина, появляется скоростная погрешность из-за возникающей в обмотках ЭДС вращения. Эта погрешность увеличивается с ростом угловой скорости. Поэтому рабочие режимы сельсинов характеризуются ограниченным уровнем скорости по условиям допустимой скоростной погрешности.
Характеристика управления сельсина в амплитудном режиме работы, построенная по (5.5), приведена на рис. 5.2. Полученные выражения для характеристики управления и передаточного коэффициента не учитывают погрешностей, вносимых в передачу сигнала сельсином несинусоидальностью распределения магнитной индукции, асимметрией магнитопровода, неравенством параметров фаз статорной обмотки и тому подобное. Перечисленные факторы обусловливают статические погрешности, искажающие форму характеристики управления. Эти погрешности в зависимости от класса точности изготовления сельсина характеризуются определенным уровнем (пунктирные линии на рис. 5.2). Наибольшее влияние они оказывают в области малых углов, где полезный сигнал соизмерим с погрешностями. Кроме статических погрешностей при вращении сельсина, появляется скоростная погрешность из-за возникающей в обмотках ЭДС вращения. Эта погрешность увеличивается с ростом угловой скорости. Поэтому рабочие режимы сельсинов характеризуются ограниченным уровнем скорости по условиям допустимой скоростной погрешности.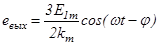 ,
,
 ,
, - расчетное полное сопротивление одной фазы стабилизирующей цепи СД и СП; xs - фазное индуктивное сопротивление рассеяния стабилизирующей обмотки одного сельсина; R - фазное активное сопротивление стабилизирующей обмотки одного сельсина; xm - сопротивление взаимной индукции между роторной и статорной обмотками, приведенное к стабилизирующей цепи; индексом СД отмечены величины, относящиеся к сельсину-датчику, а СП - к сельсину-приемнику. Если за согласованное состояние СД и СП принять взаимно перпендикулярное положение осей роторных обмоток, то рассогласование системы определится величиной Δθ = θСД - θСП + p /2. Тогда относительно Δθ характеристика управления датчика рассогласования приобретает синусоидальную зависимость
- расчетное полное сопротивление одной фазы стабилизирующей цепи СД и СП; xs - фазное индуктивное сопротивление рассеяния стабилизирующей обмотки одного сельсина; R - фазное активное сопротивление стабилизирующей обмотки одного сельсина; xm - сопротивление взаимной индукции между роторной и статорной обмотками, приведенное к стабилизирующей цепи; индексом СД отмечены величины, относящиеся к сельсину-датчику, а СП - к сельсину-приемнику. Если за согласованное состояние СД и СП принять взаимно перпендикулярное положение осей роторных обмоток, то рассогласование системы определится величиной Δθ = θСД - θСП + p /2. Тогда относительно Δθ характеристика управления датчика рассогласования приобретает синусоидальную зависимость .
. ,
, - передаточный коэффициент датчика рассогласования, В/рад.
- передаточный коэффициент датчика рассогласования, В/рад. В/рад.
В/рад. . Диапазон измерения углов может быть увеличен до некоторого θmax, если движение валу сельсина передавать через понижающий измерительный редуктор, коэффициент передачи которого равен
. Диапазон измерения углов может быть увеличен до некоторого θmax, если движение валу сельсина передавать через понижающий измерительный редуктор, коэффициент передачи которого равен 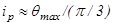 . При этом точность измерения угла уменьшается в iр раз.
. При этом точность измерения угла уменьшается в iр раз.
 , (5.6) где чертой обозначена инверсия логической переменной.
, (5.6) где чертой обозначена инверсия логической переменной.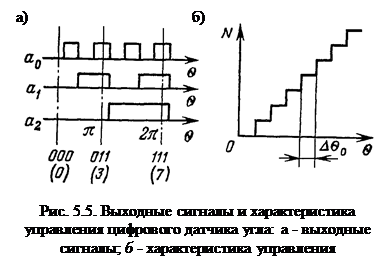 Схема, реализующая алгоритм (5.6), приведена на рис. 5.4, б. Любому углу поворота кодового диска в пределах 360° однозначно соответствует определенное сочетание единиц и нулей в выходных каналах датчика, то есть определённый числовой эквивалент угла (рис. 5.5, а). При повороте трехдорожечного кодового диска на 360о выходная величина изменяется от 000 до 111, что в десятичной системе счисления означает изменение числа от 0 до 7. В пределах интервала дискретности
Схема, реализующая алгоритм (5.6), приведена на рис. 5.4, б. Любому углу поворота кодового диска в пределах 360° однозначно соответствует определенное сочетание единиц и нулей в выходных каналах датчика, то есть определённый числовой эквивалент угла (рис. 5.5, а). При повороте трехдорожечного кодового диска на 360о выходная величина изменяется от 000 до 111, что в десятичной системе счисления означает изменение числа от 0 до 7. В пределах интервала дискретности
 ,
, - передаточный коэффициент ТГ, В/рад; k = рN/ (2p а) - конструктивная постоянная; Ф - магнитный поток возбуждения; Rтг - сопротивление якорной обмотки и щеточного контакта.
- передаточный коэффициент ТГ, В/рад; k = рN/ (2p а) - конструктивная постоянная; Ф - магнитный поток возбуждения; Rтг - сопротивление якорной обмотки и щеточного контакта.
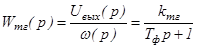 ,
, - постоянная времени фильтра.
- постоянная времени фильтра.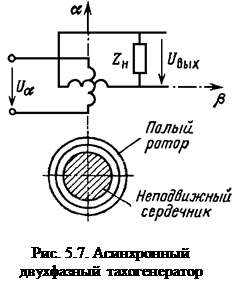 Конденсатор выполняет функцию фильтра высокочастотных относительно угловой скорости пульсаций. Чем больше Tф, тем меньше пульсации в выходном напряжении ТГ. Однако при этом ограничивается частотная полоса пропускания ТГ. При частотах передаваемого сигнала fп > 1/(2pTф) амплитудные искажения превышают 3 дБ, а фазные 45°.
Конденсатор выполняет функцию фильтра высокочастотных относительно угловой скорости пульсаций. Чем больше Tф, тем меньше пульсации в выходном напряжении ТГ. Однако при этом ограничивается частотная полоса пропускания ТГ. При частотах передаваемого сигнала fп > 1/(2pTф) амплитудные искажения превышают 3 дБ, а фазные 45°.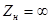 , то характеристика управления в комплексном виде имеет вид
, то характеристика управления в комплексном виде имеет вид ,
,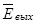 - комплексное значение выходной ЭДС тахогенератора;
- комплексное значение выходной ЭДС тахогенератора; 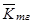 - комплексное значение коэффициента передачи тахогенератора. Даже в режиме холостого хода комплексный коэффициент передачи тахогенератора достаточно сложно зависит от активных и индуктивных сопротивлений статорных и роторных цепей и от скорости вращения ротора, то есть характеристики управления тахогенератора нелинейны. С ростом скорости ротора ухудшается линейность характеристик управления: уменьшается модуль комплексного коэффициента передачи и уменьшается его фаза, как показано на рис. 5.8 жирными линиями. Чем меньше собственное сопротивление обмотки возбуждения, тем меньшие искажения имеют характеристики ТГ. В пределе, когда сопротивление обмотки возбуждения будет равно нулю, регулировочные характеристики линейны и комплексный коэффициент передачи
- комплексное значение коэффициента передачи тахогенератора. Даже в режиме холостого хода комплексный коэффициент передачи тахогенератора достаточно сложно зависит от активных и индуктивных сопротивлений статорных и роторных цепей и от скорости вращения ротора, то есть характеристики управления тахогенератора нелинейны. С ростом скорости ротора ухудшается линейность характеристик управления: уменьшается модуль комплексного коэффициента передачи и уменьшается его фаза, как показано на рис. 5.8 жирными линиями. Чем меньше собственное сопротивление обмотки возбуждения, тем меньшие искажения имеют характеристики ТГ. В пределе, когда сопротивление обмотки возбуждения будет равно нулю, регулировочные характеристики линейны и комплексный коэффициент передачи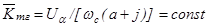 ;
;
 ;
;  ,
, Полоса пропускания асинхронного ТГ ограничена частотой питающей сети. Поэтому для быстродействующих систем используются ТГ с повышенной частотой питания. В целом асинхронные тахогенераторы отличаются высокой точностью. Линейность характеристик ТГ, применяемых в системах автоматики и счетно-решающих устройствах, характеризуется погрешностью менее 0,5 %. По сравнению с ТГ постоянного тока, асинхронный тахогенератор обладает существенно меньшим передаточным коэффициентом.
Полоса пропускания асинхронного ТГ ограничена частотой питающей сети. Поэтому для быстродействующих систем используются ТГ с повышенной частотой питания. В целом асинхронные тахогенераторы отличаются высокой точностью. Линейность характеристик ТГ, применяемых в системах автоматики и счетно-решающих устройствах, характеризуется погрешностью менее 0,5 %. По сравнению с ТГ постоянного тока, асинхронный тахогенератор обладает существенно меньшим передаточным коэффициентом. Датчик импульсов может быть выполнен, например, на основе фотоэлектрического кодового диска. В любом варианте датчик импульсов реверсивного ТГ вырабатывает две серии импульсов, сдвинутых по фазе на p /2, которые используются для определения угловой скорости и ее знака. На рис. 5.10 изображен кодовый диск фотоэлектрического датчика импульсов. На двух дорожках расположены пропускающие свет щели. Свет от источников ИС1 и ИС2 через щели попадает на фотодиоды BL1 и BL2, которые при этом открыты и пропускают ток. Когда щель выходит из луча света, фотодиоды запирают цепь. При вращении диска с угловой скоростью w BL1 и BL2 дают чередование максимального и минимального сигналов с частотой
Датчик импульсов может быть выполнен, например, на основе фотоэлектрического кодового диска. В любом варианте датчик импульсов реверсивного ТГ вырабатывает две серии импульсов, сдвинутых по фазе на p /2, которые используются для определения угловой скорости и ее знака. На рис. 5.10 изображен кодовый диск фотоэлектрического датчика импульсов. На двух дорожках расположены пропускающие свет щели. Свет от источников ИС1 и ИС2 через щели попадает на фотодиоды BL1 и BL2, которые при этом открыты и пропускают ток. Когда щель выходит из луча света, фотодиоды запирают цепь. При вращении диска с угловой скоростью w BL1 и BL2 дают чередование максимального и минимального сигналов с частотой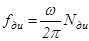 ,
, Токовый сигнал фотодиода изменяется по форме и амплитуде при изменении скорости вращения. Поэтому для получения стабильных сигналов с неизменными амплитудой и продолжительностью в состав датчика импульсов входит узел формирования выходных импульсов (рис. 5.11). В усилителе У1 токовый сигнал фотодиода BL1 усиливается и симметрируется по полярности Uу1. Усилитель, собранный на транзисторах VT1 и VT2 и работающий с использованием положительной связи в релейном режиме, дает на выходе прямоугольные импульсы U1 с постоянной амплитудой, равной напряжению питания Uп,но с переменной продолжительностью. Выходной импульс Uвых с неизменными амплитудой и продолжительностью t формируется с помощью одновибратора S. Диаграмма работы описанного узла приведена на рис. 5.12. Аналогичный узел имеется и для импульсов второй дорожки кодового диска с фотодиодом BL2. Для каждого направления вращения в датчике импульсов имеется свой выходной канал.
Токовый сигнал фотодиода изменяется по форме и амплитуде при изменении скорости вращения. Поэтому для получения стабильных сигналов с неизменными амплитудой и продолжительностью в состав датчика импульсов входит узел формирования выходных импульсов (рис. 5.11). В усилителе У1 токовый сигнал фотодиода BL1 усиливается и симметрируется по полярности Uу1. Усилитель, собранный на транзисторах VT1 и VT2 и работающий с использованием положительной связи в релейном режиме, дает на выходе прямоугольные импульсы U1 с постоянной амплитудой, равной напряжению питания Uп,но с переменной продолжительностью. Выходной импульс Uвых с неизменными амплитудой и продолжительностью t формируется с помощью одновибратора S. Диаграмма работы описанного узла приведена на рис. 5.12. Аналогичный узел имеется и для импульсов второй дорожки кодового диска с фотодиодом BL2. Для каждого направления вращения в датчике импульсов имеется свой выходной канал. Формирование цифрового кода на выходе датчика скорости с помощью счетчика может выполняться двумя способами. В соответствии с первым способом на заданном периоде измерения Т счетчик подсчитывает число импульсов, которое будет характеризовать среднее значение скорости:
Формирование цифрового кода на выходе датчика скорости с помощью счетчика может выполняться двумя способами. В соответствии с первым способом на заданном периоде измерения Т счетчик подсчитывает число импульсов, которое будет характеризовать среднее значение скорости: .
. Увеличение значения Т для уменьшения погрешности при низких скоростях нежелательно, так как при этом возрастает дискретность по времени и увеличивается расхождение между средним и мгновенным значениями скорости, что может затруднить использование ЦДС всистемах управления.
Увеличение значения Т для уменьшения погрешности при низких скоростях нежелательно, так как при этом возрастает дискретность по времени и увеличивается расхождение между средним и мгновенным значениями скорости, что может затруднить использование ЦДС всистемах управления.


