
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 15. Моделирование и идентификация динамических систем.Содержание книги
Поиск на нашем сайте
Понятие "динамическая система" шире, чем понятие "промышленный объект". Известно что, динамические модели объектов управления являются более сложными, они отражают влияние на объект временных характеристик не только в данный момент, но и в прошлые моменты времени. Состояние динамической системы описывается совокупностью физических переменных состояния x 1(t),…, xn (t), характеризующих поведение системы в будущем при условии, если известно состояние в исходный момент времени и приложенные к системе воздействия.
При этом переменные состояния x 1(t), x 2(t)…, xn (t) позволяют по начальным значениям переменных x 1(t 0), x 2(t 0)…, xn (t 0), т.е. в начальный момент времени t 0, и заданным воздействиям u 1(t),…, um (t) при t ³ t 0 определить будущие значения переменных состояния и выходных переменных (рис.4.1). Корректная постановка математической задачи синтеза оптимального управления динамическими системами предполагает, что у разработчика системы имеется такая информация: − переменные, описывающие параметры состояния системы и параметры управления; − математическая модель процесса функционирования динамической системы объекта управления; − одномерная или многомерная функция - критерий качества управления, с помощью которого выражается цель управления; − математические соотношения, описывающие ограничения, налагаемые на переменные состояния или управления. Обычно на практике рассматриваются системы, процесс функционирования которых протекает во времени. Кроме того, современный подход к математическому описанию динамических систем состоит в описании систем в пространстве состояний. Аргументом входных и выходных сигналов системы может служить время, пространственные координаты, а также некоторые специальные переменные. Любая математическая модель динамической системы, в конечном счете, строится по результатам наблюдений за входными и выходными сигналами. Такую процедуру, принято называть идентификацией, в данном случае, идентификацией динамических объектов. Активная идентификация предполагает, что исследователь выбирает рациональные моменты (или периоды) наблюдений за входами и выходами системы, задает определенные начальные условия или подает на вход специальный управляющий (тестирующий или пробный) сигнал и т.д. Следовательно, активная идентификация - это логическое развитие концепции активного эксперимента в статике.
Математическая модель в данном случае рассматривается как упрощенное отображение существенных сторон реальной системы, выраженное в математической форме. При идентификации динамических систем под математической моделью понимают правило преобразования входных сигналов Х в выходные сигналы Р. Преобразование входных сигналов в выходные, т. е. математическую модель системы, можно представить в общем виде с помощью некоторого оператора системы А { }: Р= А {Х } Х Р
Вектор входных сигналов Вектор выходных сигналов
Рис. Принципиальная блок-схема системы Под символом А { } понимаются любые математические действия (алгебраические операции, дифференцирование, интегрирование, решение алгебраических, дифференциальных, интегральных и любых других функциональных уравнений, а также логические действия). Таким образом, оператор представляет собой совокупность математических и логических операций, позволяющих установить соответствие между входными и выходными сигналами. Существует большое разнообразие математических моделей производственных объектов. Их можно классифицировать по самым различным признакам. За основу классификации можно принять, в первую очередь, те или иные признаки (свойства) оператора A{ }. Оператор системы преобразует векторную функцию Х(t) в векторную функцию Р(t). Такой оператор сам по себе может зависеть от времени t: A=A(t)=A Модели подобного типа называют динамическими (временными). Если свойства преобразования входных сигналов (функций), т. е. структура и свойства оператора А { }, не изменяются со временем, то динамическую систему (модель) называют стационарной. В противном случае ее именуют нестационарной. Реакция стационарной системы на любой заданный тип возмущения зависит только от интервала времени между моментом начала действия входного возмущения и данным моментом времени. Если процесс развивается одновременно и во времени, и в пространстве, например, по одной координате L, то оператор может преобразовывать входную векторную функцию z (t,L) в выходную векторную функцию
A=A(t,L)=A t,L Эти модели называют пространственно-временными. К простейшим динамическим моделям относят, например, регрессионную модель. y = a0 + a1x1(t) + a2x2(t) +….. + anxn(t)
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.7.232 (0.009 с.) |

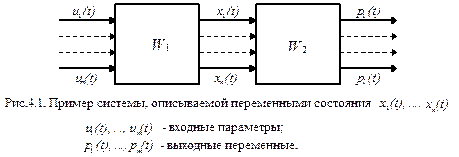

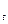
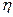 (t, L), и сам по себе он тоже может зависеть от обоих этих аргументов:
(t, L), и сам по себе он тоже может зависеть от обоих этих аргументов:


