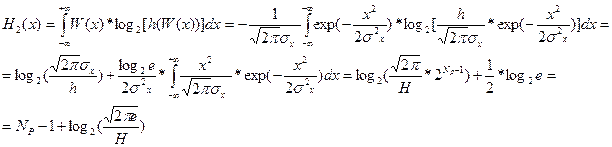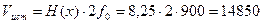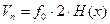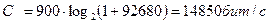Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет числа разрядов квантования.Содержание книги Поиск на нашем сайте
Таким образом, задавшись допустимым значением относительной ошибки d3, можно найти число разрядов двоичного кода, обеспечивающее заданную точность преобразования: N р = Е где Е (х) – целая часть дробного числа х.
Подставим значения: N р = Е Расчет длительности импульса двоичного кода. После определения частоты дискретизации и числа разрядов двоичного кода можно определить длительность импульса кодовой последовательности:
Где: tС – длительность временного интервала, предназначенного для передачи сигнлов синхронизации. tИ-длительность импульса кодовой последовательности.
При условии, что
Расчет ширины спектра сигнала, модулированного двоичным кодом. В системах, которые являются предметом настоящей курсовой работы, предусмотрено использование сигналов с активной паузой за счёт изменения фазы на p или частоты на некоторое значение Dwм. Скачкообразное изменение параметра сигнала называется манипуляцией в отличие от модуляции, которая предусматривает плавное изменение параметра. Таким образом, в результате манипуляции двоичная последовательность кодовых символов с различными фазами (частотами) может быть представлена суммой двух импульсных последовательностей с различными начальными фазами или частотами. Поскольку характер последовательностей определяется реализацией сообщения, каждую из них следует считать случайным процессом с характерной для последовательности прямоугольных импульсов функцией корреляции в виде гармонической функции (косинуса) с огибающей треугольной формы. Спектральная плотность мощности такой последовательности имеет вид функции (sin2 х)/ х 2, максимум которой находится на несущей частоте, а ширина главного лепестка по первым нулям спектральной плотности равна D f 0 = 2/tu. На практике и в литературе обычно ширина спектра определяется полосой частот, в которой сосредоточено 80-90% энергии (мощности) сигнала. По этому критерию для радиоимпульса прямоугольной формы обычно принимается D f с» 1/tu
Это же значение имеет ширина спектра всего фазоимитированного сигнала, т.к. несущие частоты обеих последовательностей совпадают. Для сигнала с частотной модуляцией ширина спектра увеличивается по сравнению с предыдущим значением на расстояние между несущими последовательностей «единц» и «нулей»:
При условии
Расчет информационных характеристик источника сообщения и канала связи. Необходимо рассчитать энтропию источника сообщения, оценить его избыточность, производительность. Для расчёта энтропии целесообразнее всего воспользоваться приближённой формулой, которая является достаточно точной при большом числе уровней квантования: Н (х) где W (х) - плотность вероятности сообщения; h = 2 U М × 2- N р - значение интервала квантования, которое можно рассчитать по ранее полученным результатам; U М – порог ограничения сообщения. При записи плотности вероятности сообщения следует учесть, что эффективное значение сообщения равно одному вольту (sх = 1в), а при интегрировании для всех распределений, кроме первого типа, пределы следует брать бесконечными.
Запишем для второго распределения:
Тогда для третьего распределения имеем:
Для оценки избыточности сначала рекомендуется рассчитать информационную насыщенность сообщения: I Н (х) = Н (х)/ Н МАКС, где Н МАКС – максимальная энтропия источника, достигаемая при равномерном распределении.
Найдем производительность источника
Информационная насыщенность сообщения
Избыточность
Расчёт отношений мощностей сигнала и помехи, необходимых для обеспечения заданного качества приёма.
Пропускная способность
Определение отношения сигнал \ шум
Тогда пропускная способность канала связи равна:
|
|||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.27.154 (0.009 с.) |

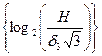 + 1,
+ 1,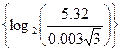 + 1 = 11 разрядов.
+ 1 = 11 разрядов. ,
, получим:
получим:


 ,
, кГц
кГц [бит/симв],
[бит/симв],