
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Датчик температуры на основе металлических проводниковСодержание книги
Поиск на нашем сайте
Датчик температуры включён в Мост Уитстона представленный на рисунке 15. При температуре 0°С Мост Уитстона сбалансирован.
Рисунок 15 − Мост Уитстона
Необходимо: − построить график зависимости − определить напряжение − определить какие диапазоны температур при изменении -40 и +100°С попадают в область относительной погрешности измерения напряжения Исходные данные: − температурный коэффициент, − сопротивление металлического проводника при температуре 0°С, − напряжение питания Моста Уитстона, Сопротивление датчика температуры, выполненного на основе металлического проводника, определяется выражением 13.
где
Напряжение между точками 1 и 2 на схеме (рисунок 15) определяется формулой 14.
При условии баланса Моста Уитстона Из схемы представленной на рисунке 15 и выражений 13 и 14 получаем зависимости График зависимости температуры окружающей среды от напряжения
Рисунок 16 − График зависимости температуры окружающей среды от напряжения
Определить напряжение Температура окружающей среды По формуле 13 определяем значения сопротивлений
По формуле 14 определяем значения
С учётом заданной 5% погрешности вольтметра, определим фактические интервалы значений напряжения
Определим какие диапазоны температур при изменении -40 и +100°С попадают в область относительной погрешности измерения напряжения Итак, полученные диапазоны искомых температур T = 218,995…420,279К и 223,637…402,897 К. Терморезистор на основе полупроводникового элемента Необходимо: − построить характеристику выражением − выбрать в диапазоне температур [
− построить зависимость скорости изменения напряжения
Рисунок 17 − Схема цепи
Исходные данные: − сопротивление терморезистора при заданной температуре, − температура при − константа материала терморезистора, B = 2240 К; − напряжение, На рисунке 18 представлена характеристика
Рисунок 18 − Характеристика
Определяем среднюю температуру диапазона [ Значения
Сопротивление линеаризирующего резистора определяем по формуле 15.
Линеаризированная кривая в заданном температурном диапазоне представлена на рисунке 19.
Рисунок 19 − Линеаризированная кривая в заданном температурном диапазоне
Сопротивление резистора
Сопротивление R определяем по формуле 17.
Зависимость скорости изменения напряжения задана выражением
График скорости изменения напряжения от времени представлен на рисунке 20.
Рисунок 20 − График скорости изменения напряжения от времени Пьезоэлектрический датчик Цилиндрический пьезоэлектрический датчик изготовлен из титана бария и представлен на рисунке 21.
Рисунок 21 − Цилиндрический пьезоэлектрический датчик
Механическая сила F воздействует на датчик вдоль его продольной оси, в результате чего, на противоположных краях кристалла появляется ЭДС. Необходимо: − найти максимальную ЭДС датчика; − определить максимальное входное напряжение на усилителе, если датчик включён по схеме приведённой на рисунке 22; − определить модуль чувствительности схемы;
− определить максимальное выходное напряжение с усилителя; Исходные данные: − пьезоэлектрический модуль, − механическая сила, − частота, f = 10000 Гц; − радиус кристалла, − высота кристалла, − диэлектрическая составляющая, − входное сопротивление усилителя, − входная ёмкость усилителя, − коэффициент усиления, K = 10; − диэлектрическая постоянная,
Рисунок 22 − Эквивалентная схема пьезоэлектрического датчика
Определяем выходную ёмкость с датчика по формуле 18.
Механическое воздействие подчиняется заданному закону
Определяем максимальную ЭДС датчика по формуле 19.
Определяем максимальное входное напряжение по формуле 20.
Модуль чувствительности заданной схемы определяется заданным выражением 21.
где График изменения модуля чувствительности представлен на рисунке 23.
Рисунок 23 − График изменения модуля чувствительности
Определяем максимальное выходное напряжение с усилителя по формуле 22.
3.3.7 Преобразование экспериментальных данных в аналитическую функцию Необходимо: − по полученным экспериментальным данным с датчика, отображающих зависимость выходного напряжения от массового расхода воздуха, построить аналитическую функцию для дальнейшего расчёта микроконтроллером промежуточных значений. − построить график относительной погрешности расхождения экспериментальных данных выходного напряжения от аналитических. Исходные данные: − экспериментальные данные выходного напряжения, − экспериментальные данные расхода воздуха, M = [0; 1; 2; 3; 4; 5; 6] г/сек. Для получения аналитической зависимости используем метод наименьших квадратов. Аналитическая зависимость должна иметь вид Общая формула метода наименьших квадратов – формула 23.
Прологарифмируем экспериментальные значения выходного напряжения, − возьмём натуральный логарифм от каждого значения из массива Наёдём коэффициенты a и b из системы уравнений 23. Здесь значения В результате решения системы уравнений получаем значения искомых коэффициентов: a = -0,85 и b = 2,501. Аналитическая зависимость
Рисунок 24 − График аналитической зависимости
Найдём относительную погрешность расхождения экспериментальных данных выходного напряжения от аналитических. Отметим, что в качестве экспериментальных данных при расчёте погрешностей используем массив Итак, имеем Относительную погрешность определяем по формуле 24.
Полученные значения относительной погрешности
|
||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.232.244 (0.008 с.) |


 ;
; при температурах -40 и +100°С.
при температурах -40 и +100°С.
 ;
; Ом;
Ом; В;
В; , (13)
, (13) − температура окружающей среды, °С.
− температура окружающей среды, °С. . (14)
. (14)
 , где
, где  .
.
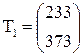 К.
К. при заданных значениях
при заданных значениях  Ом,
Ом, Ом.
Ом.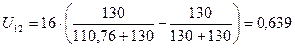 В,
В, В.
В.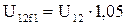 ,
,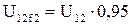 ,
, В,
В, В,
В, В,
В,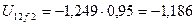 В.
В. , где
, где  .
. терморезистора, выполненного на основе полупроводникового элемента, если его сопротивление определяется
терморезистора, выполненного на основе полупроводникового элемента, если его сопротивление определяется ;
; …
…  ] сопротивление линеаризирующего резистора
] сопротивление линеаризирующего резистора  включённого параллельно терморезистору и построить в указанном температурном диапазоне линеаризированную кривую.
включённого параллельно терморезистору и построить в указанном температурном диапазоне линеаризированную кривую. в диапазоне [
в диапазоне [ 
 Ом;
Ом; Ом,
Ом, 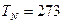 К;
К; В.
В.
 . Средняя температура определяется в точке, в которой касательная к кривой
. Средняя температура определяется в точке, в которой касательная к кривой  К при
К при 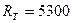 Ом.
Ом. и
и 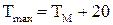 соответственно
соответственно К,
К, К.
К.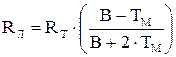 , (15)
, (15) Ом.
Ом.
 определяем по формуле 16.
определяем по формуле 16. , (16)
, (16) Ом.
Ом. , (17)
, (17) Ом.
Ом. .
.

 Кл/Н;
Кл/Н; Н;
Н;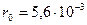 м;
м; м;
м; ;
; Ом;
Ом; Ф;
Ф;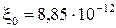 .
.
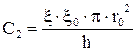 , (18)
, (18) Ф.
Ф. .
. , (19)
, (19) .
.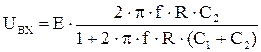 , (20)
, (20) В.
В. , (21)
, (21) .
.
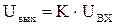 , (22)
, (22) В.
В. =[7,389; 3,857; 2,014; 1,051; 0,549; 0,287; 0,150] мВ.
=[7,389; 3,857; 2,014; 1,051; 0,549; 0,287; 0,150] мВ. , где a и b − коэффициенты.
, где a и b − коэффициенты. , (23)
, (23) соответственно равны данным из массива M; значения
соответственно равны данным из массива M; значения  соответственно равны данным из массива
соответственно равны данным из массива 
 . В качестве истинных значений принимаем аналитические данные.
. В качестве истинных значений принимаем аналитические данные. , (24)
, (24) .
.


