
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графо-аналитический метод Катца и СтендингаСодержание книги Поиск на нашем сайте
а) Определяем плотность жидкости при стандартных условиях
где xi, Mi, ri - мольная доля, молекулярная масса и плотность i-го компонента. в) Определяем поправки к стандартной плотности на давление Drр и температуру Drт. с) Находим плотность насыщенного конденсата при заданных давлении и температуре r=rст+Drр-Drт. (2.10)
2.2.2. Корреляционная зависимость приведённой плотности rпр от среднекритического коэффициента сверхсжимаемости zск. Порядок расчета
Здесь: а) ркр,7+ и Ткр,7+ - определяются по формулам (2.7) или части 1
в) w7+ - находится или по правилу аддитивности при известном групповом составе конденсата, или берётся просто w7 из таблиц, или при известных температурах кипения и критической находится по формуле Эдмистера
)а для углеводородов парафинового ряда (до С7, включительно) Tкр /Tкип можно определить по корреляционной зависимости Гуревича
с) zcк - среднекритический коэффициент сжимаемости жидкой смеси
где zкр,i - критический коэффициент сжимаемости i-го компонента и определяется из таблиц или по формуле Ганна и Ямаду zкр,i= 0,2918 - 0,0928wi; (2.14) d) Критический молярный объём i-го компонента находим из уравнения состояния
где критические параметры компонент берём из таблиц. e) Приведённая температура насыщенной жидкости
f) Приведённая плотность определяется по формуле Викса
g) Плотность насыщенного конденсата
2.3. Пример Определить плотность насыщенного конденсата по приведённому давлению и температуре, используя зависимость приведённой плотности от критического коэффициента сжимаемости. Компонентный состав конденсата в мольных долях при абсолютном давлении р = 70ата и температуре Т=3999,8 К и результаты расчетов приведены в таблице
`
zкр,7+в=0,2918-0,0928×0,855=0,21; Vкр,7+в=0,21×82,057×775/13,35=1000 см3/моль; Тпр=399,8/617,29=0,647;
r=215,46×2,99/744,81=0,863 г/см3.
4. Контрольные задания Найти коэффициент сверхсжимаемости и плотности насыщенного конденсата для вариантов первого задания.
Вязкость
Для расчета динамической вязкости природных газов m следует использовать соотношения Тодоса, которые в зависимости от величины приведённой плотности rпр=r/rкр имеют вид: а) rпр> 2
b) 0,3<rпр£ 2
c) rпр£ 0,3
где Коэффициент динамической вязкости m0 при атмосферном давлении в зависимости от температуры рассчитывается по зависимостям: а) при Тпр³ 1,5
при Тпр< 1,5
В формулах (2), (3): ркр - 0,1МПа, m - мкПа×с, Т - оК. Для расчета вязкости в зависимости от температуры при атмосферном давлении можно использовать и следующие зависимости:
или
где t- 0С, h-м Па .с. Погрешность расчетов по формулам (3.3), (3.3..1) при 12 £ Мсм£100 и 283 £ Т£477 К не превышает 5%. Порядок расчета m:
При содержании азота в при родном газе более 5% следует учитывать его влияние на вязкость газа по правилу аддитивности:
где уа - молярная доля азота в составе смеси; mа, mу - коэффициенты динамической вязкости азота и углеводородной части, соответственно. Коэффициент динамической вязкости углеводородного конденсата при различных давлениях и температурах приближенно можно рассчитать по эмпирической формуле Муталибова, Шубина и Абдурахманова:
при 0,1 £ р£50,0 МПа и 30 £ t£200 0C.
Теплоёмкость
При изобарическом процессе зависимость молярной теплоёмкости углеводородных компонентов природных газов при атмосферном давлении и различной температуре приближенно можно выразить следующим уравнением
где t - температура, 0С; Mi - молекулярная масса углеводорода, являющегося компонентом природного газа (от метана до гексана включительно). Погрешность в интервале температур от -40 до +1200С: для СН4 - С5Н12 – не более5%, для С6Н14-С7Н16 – не превышает 10%. При изобарическом процессе молярная теплоёмкость неуглеводородных компонентов природных газов (азота, углекислого газа, сероводорода) равна примерно половине теплоёмкости углеводорода с одинаковой молекулярной массой при одной и той же температуре, которая рассчитывается по уравнению (7). Теплоёмкость смесей рассчитывается по правилу аддитивности
где yi - молярная доля i-го компонента в смеси; Ср,i - молярная теплоёмкость i-го компонента. Молярная теплоёмкость природных газов зависит от давления и температуры
где DСр(р,t) - изотермическая поправка теплоёмкости на давление. Поправка находится из графика по приведённым значениям давления и температуры или аналитически из уравнения состояния, на пример, Пенга-Робинсона
Здесь:
Для приближенных расчетов при 0,02 £ рпр £ 4 и 1,3 £ Тпр £ 2,5 поправку DСр(р,t) можно рассчитать с погрешностью, не превышающей 10% по формуле
При изобарическом процессе молярную теплоёмкость природного газа можно рассчитать и по формуле, предложенной Гухманом и Нагаревой
Для расчета температуры и мощности в процессах адиабатного расширения и сжатия природных газов необходимо строго математически определить значения температурного КТ и объёмного КV коэффициентов адиабаты. Последнее возможно при определении частных производных коэффициента сверхсжимаемости соотношениями (1.30) и подстановкой их в зависимости:
Коэффициент адиабаты природного газа находится по формуле
или используя аппроксимацию вычитаемого в знаменателе
Если в расчетах необходимо иметь не молярную, а массовую теплоёмкость, то следует значение молярной теплоёмкости разделить на молекулярную массу газа Мi, т.е на массу киломоля i-го компонента, кг/моль.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.184.197 (0.006 с.) |


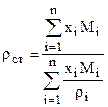 , (2.9)
, (2.9)

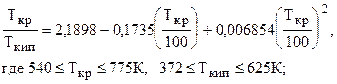 (2.12)
(2.12)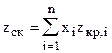 , (2.13)
, (2.13) , (2.15)
, (2.15) (2.16)
(2.16)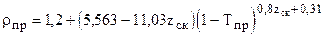 . (2.17)
. (2.17) (2.180
(2.180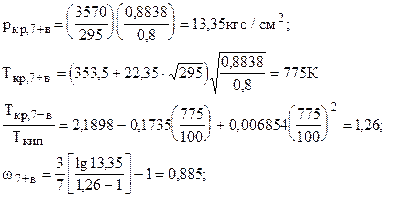
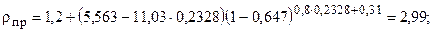

 (3.1)
(3.1)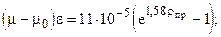
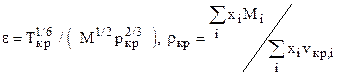 .
.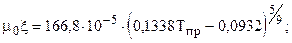 (3.2)
(3.2)
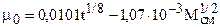 (3.3)
(3.3) , (3.3.1)
, (3.3.1)
 , (3.4)
, (3.4) , (3.5)
, (3.5) , (3.6)
, (3.6) , (3.7)
, (3.7)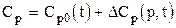 , (3.8)
, (3.8) (3.9)
(3.9) (3.10)
(3.10) [кДж/(кмоль К)]. (3.11)
[кДж/(кмоль К)]. (3.11) [кДж/(кмоль К)]. (3.12)
[кДж/(кмоль К)]. (3.12) , (3.13)
, (3.13)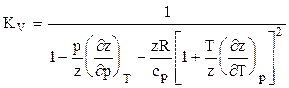 , (3.14)
, (3.14)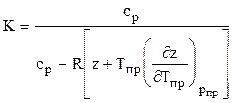 (3.15)
(3.15) (3.16)
(3.16)


