
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комп’ютерних лабораторних робітСодержание книги
Поиск на нашем сайте
Порядок виконання робіт: 1. Для допуску до роботи необхідно відповісти на декілька контрольних запитань. Тільки в разі правильної відповіді на всі запитання Ви будете допущені до роботи. 2. На другому етапі виконується робота. Експериментальні дані і результати обчислень заносять в протокол. Після того, як всі досліди будуть проведені і всі графи протоколу випробувань заповнені, слід повернутися в головне вікно браузера і натиснути на кнопку «далі» для перевірки результатів. У тому випадку, якщо всі значення були заміряні або обчислені правильно, Ви перейдете до третього етапу. У протилежному випадку неправильно виконані досліди будуть помічені червоним хрестиком (правильні – зеленою галочкою). Неправильно виконані досліди треба провести наново. 3. Після успішного виконання лабораторної роботи Вам буде запропоновано відповісти на декілька контрольних запитань. Після закінчення тесту Вам буде виставлено результуючу оцінку.
Примітки до заповнення таблиці: 1. При введенні десяткових дробів ціла частина відділяється від дробової за допомогою крапки. 2. Введення значень, аналогічних Примітка: E – латинська літера. ФІЗИЧНІ ОСНОВИ МЕХАНІКИ. МЕХАНІЧНІ КОЛИВАННЯ
ЛАБОРАТОРНА РОБОТА №2.1
Мета роботи: вивчення законів пружного та непружного зіткнень.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Зіткнення – це короткочасна взаємодія, за якої тіла безпосередньо дотикаються одне до одного. У цій роботі вивчається центральне зіткнення куль. Зіткнення називається центральним, якщо вектори швидкостей куль до удару направлені по прямій, що проходить через їх центри. Абсолютно пружним називається таке зіткнення, в разі якого механічна енергія тіл, що стикаються, зберігається. За умови абсолютно пружного центрального удару кінетична енергія куль, що стикаються, до удару повинна дорівнювати їх кінетичній енергії після удару. У разі абсолютно непружного удару кінетична енергія повністю або частково перетворюється на внутрішню енергію. Після удару тіла або рухаються з однаковою швидкістю, або знаходяться в стані спокою. Закон збереження механічної енергії не виконується.
Абсолютно пружні та непружні зіткнення – це ідеальні випадки. На практиці вони можуть бути реалізовані лише з певним ступенем наближення. У довільному випадку ударів куль справедливі закони збереження імпульсу та енергії:
де У разі абсолютно пружного удару Введемо критерій пружності співударяння куль. Енергетичний коефіцієнт відновлення дорівнює відношенню повної кінетичної енергії системи після удару до повної кінетичної енергії до удару:
Для абсолютно пружного співударяння У нашій установці одна із куль до удару буде знаходитися в стані спокою (
Формула (2.1.4) виводиться з використанням (2.1.1) – (2.1.3). Для довільних співударянь куль справедлива нерівність
ОПИС ВИМІРЮВАЛЬНОЇ УСТАНОВКИ І МЕТОДИКА ВИМІРЮВАНЬ
На стійкій підставці закріплена вертикальна труба (1) з підвісами для куль (2) (рис. 2.1.1). Одна з куль (масою Виразимо енергетичний коефіцієнт відновлення через кути відхилення куль до і після удару. Припустимо, що кулю масою
де Після удару кулі розходяться, піднімаючись на висоту
Підставивши (2.1.6) - (2.1.8) у (2.1.3), одержимо
Знаючи вираз для
де Враховуючи, що
З формул (2.1.6) - (2.1.8) випливає, що
Залежність
Знак плюс в правій частині (2.1.11) відповідає випадку, коли куля
ПОРЯДОК ВИКОНАННЯ РОБОТИ
У роботі ставляться дві задачі: 1. Визначення енергетичного коефіцієнта відновлення для різних пар куль, що стикаються. 2. Перевірка закону збереження імпульсу при ударі.
Проведіть досліди щодо зіткнення різних пар куль. У кожному досліді виміряйте кути відхилення
Таблиця 2.1.1
Запитання, що часто виникають. 1. Як провести дослід? Спочатку треба вибрати кулі, які будуть стикатися. Далі треба відхилити праву кулю на довільний кут (цей кут потрібно запам’ятати) і відпустити кулю. Після того як кулі зупиняться, потрібно занести експериментальні дані в протокол дослідів і обчислити шукані величини. 2. Як вибрати кулю? Для зміни кулі потрібно навести курсор миші на кулю, яка знаходиться в коробці і натиснути ліву кнопку миші. Кулю з лівого боку вибирають з лівої коробки, з правого – з правої. 3. Як відхилити кулю на довільний кут? Для того, щоб відхилити кулю, закріплену до підвісу, слід навести на неї курсор миші, натиснути ліву кнопку миші, і, утримуючи її, відхилити кулю на довільний кут. Кут зручно заміряти за нижньою шкалою.
КОНТРОЛЬНІ ЗАПИТАННЯ
До експерименту
1. Кульку масою · 1. · · 2. 2. Імпульси двох тіл однакові · 1. · · 2. 3. Кінетичні енергії тіл з масами · · · 4. Імпульси тіл з масами · · · 5. Імпульси двох тіл відрізняються у два рази · 2. · 1. · 4. 6. Чи може тіло мати енергію, не маючи імпульсу? · Так. · Ні. · Немає однозначної відповіді. 7. Для якого зіткнення справедливий закон збереження механічної енергії? · Для абсолютно пружного. · Для абсолютно непружного. · Для кожного. 8. Чи може тіло мати імпульс і не мати при цьому енергії? · Так. · Ні. · Немає однозначної відповіді. 9. Для якого зіткнення коефіцієнт енергетичного відновлення · Для абсолютно пружного. · Для абсолютно непружного. · Для кожного. 10. Для якого зіткнення виконується закон збереження імпульсу? · Для абсолютно пружного. · Для абсолютно непружного. · Для кожного. Після експерименту
1. На нерухому кулю налітає зі швидкістю
· · · 2. Дві більярдних кулі з однаковими масами, що рухаються назустріч одна одній, зазнають абсолютно пружного зіткнення. Швидкість першої кулі до зіткнення 2 м/с, другої 3 м/с. Знайти швидкість першої кулі після зіткнення. · 3 м/с. · 1 м/с. · 5 м/с. 3. Дві кулі масами 1.5 кг і1.0 кг рухаються в одній площині зі швидкістю 2 м/с і 4 м/с, відповідно. Вектори швидкостей куль утворюють · 2 м/с. · 3 м/с. · 0.25 м/с. 4. Які закони використовуються для виведення робочих формул цієї лабораторної роботи? · Закони Ньютона, закон збереження імпульсу. · Закони Ньютона, закони збереження енергії. · Закони збереження імпульсу і енергії. 5. У досліді І куля масою · 1/3. · 2. · 1/2. 6. Куля масою · · · 7. Тіло масою · 3 Дж. · 6 Дж. · Немає вірної відповіді. 8. Частинка 1 абсолютно пружно зіткнулася з частинкою 2, яка не рухалась до удару. Знайти відношення мас частинок · 1. · 3. · Немає вірної відповіді. 9. Дві непружніх кулі з масами · 6 м/с. · 3.6 м/с. · Немає вірної відповіді. 10. Чи може коефіцієнт енергетичного відновлення · Не може. · Так, якщо удар абсолютно непружний. · Так, якщо удар абсолютно пружний.
ЛАБОРАТОРНА РОБОТА №2.2
Мета роботи: перевірити основний закон динаміки обертального руху за допомогою маятника Обербека.
Маятник Обербека складається зі шківа і стрижнів, закріплених на одній нерухомій горизонтальній осі, що проходить через центр симетрії системи. Відносно цієї осі маятник може обертатися. На стрижні насаджені однакові за масою тягарці
ТЕОРЕТИЧНІ ВІДОМОСТІ Основний закон динаміки твердого тіла, що обертається навколо нерухомої осі, має вигляд:
де Маятник Обербека обертається під дією моменту сили натягу нитки Момент інерції маятника дорівнює Рівняння (2.2.1) перепишемо у вигляді:
звідси
Прискорення
Якщо нитка пересувається по шківу без проковзування, то тангенціальне прискорення точок на поверхні шківа Тому кутове прискорення маятника
Момент сили тертя визначаємо із закону збереження енергії. Тягарець
З іншого боку
де N – кількість обертів шківа. Враховуючи це, перепишемо (2.2.5):
звідси:
Позначимо
Тоді
Підставивши (2.2.3), (2.2.4), (2.2.7) в (2.2.2), одержимо
ПОРЯДОК ВИКОНАННЯ РОБОТИ Виберіть тягарець Таблиця 2.2.1
Запитання, що часто виникають. 1. Як вибрати тягарець 2. Як змінити положення тягарців на маятнику? Положення тягарців на маятнику змінюється шляхом натиснення лівої кнопки миші.
КОНТРОЛЬНІ ЗАПИТАННЯ До експерименту
1. Що відбудеться з моментом інерції маятника Обербека, якщо тягарець масою · Збільшиться. · Зменшиться. · Не зміниться. 2. Які сили створюють обертальний момент маятника Обербека? · Сила ваги і сила тертя. · Сила ваги і натягу нитки. · Сила натягу нитки і сила тертя. 3. Який зміст має величина · Момент інерції тягарця масою · Момент інерції маятника Обербека без тягарців. · Момент інерції шківа. 4. Точка обертається по колу радіусом · · · 5. Який закон перевіряється за допомогою маятника Обербека? · Закон збереження імпульсу. · Основний закон динаміки обертального руху. · ІІ закон Ньютона. 6. На тіло, здатне обертатися навколо нерухомої осі, діють дві сили · · · 7. Як зміниться кутове прискорення маятника Обербека в разі зміни найвіддаленішого від осі обертання положення вантажів · Збільшиться. · Зменшиться. · Залишається без зміни. 8. Які величини вимірюють в експерименті з маятником Обербека для визначення прискорення · Довжина нитки · Радіус шківа · Маса тягарця 9. Які припущення про фізичні властивості нитки зроблені в цій роботі? · Довжина нитки набагато більша за радіус шківа. · Маса нитки порівнянна з масою тягарця · Можна знехтувати розтягом нитки і її масою. 10. Який закон використовується в роботі для визначення моменту сили тертя? · Закон збереження енергії. · ІІ закон Ньютона. · Закон збереження моменту імпульсу. Після експерименту 1. На шківи, що мають форму дисків з радіусами · · · 2. Після включення вентилятор, зробивши · · · 3. Маховик, що має момент інерції · · · 4. Куля масою · 350 Дж. · 250 Дж. · 100 Дж. 5. Маховик у формі диска обертається навколо осі симетрії за законом · · · 6. Діаметр диска · · · 7. Основний закон динаміки обертального руху, якщо · · · 8. Момент інерції вала масою · · · 9. Радіус вала махового колеса · · · 10. На диски, що мають радіуси · · ·
ДОДАТОК ДО ЛАБОРАТОРНОЇ РОБОТИ №2.2
ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.26.112 (0.012 с.) |

 , здійснюється таким чином 1.5E20 або
, здійснюється таким чином 1.5E20 або  вводиться так: 4.8E-12.
вводиться так: 4.8E-12.

 ,
,
 ,
,  – маси куль,
– маси куль,  ,
,  – швидкість куль до удару,
– швидкість куль до удару,  ,
,  – швидкість куль після удару,
– швидкість куль після удару,  – енергія, яка переходить у внутрішню енергію куль.
– енергія, яка переходить у внутрішню енергію куль.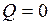 , а для абсолютно непружного удару
, а для абсолютно непружного удару  .
. .
.
 .
. ). У цьому випадку енергетичний коефіцієнт відновлення для абсолютно непружного зіткнення (
). У цьому випадку енергетичний коефіцієнт відновлення для абсолютно непружного зіткнення (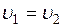 ) матиме вигляд
) матиме вигляд .
.
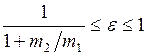
 над початковим рівнем відліку потенціальної енергії (0), потім відпускають. Безпосередньо перед ударом куля має швидкість
над початковим рівнем відліку потенціальної енергії (0), потім відпускають. Безпосередньо перед ударом куля має швидкість  .
. Згідно з законом збереження механічної енергії
Згідно з законом збереження механічної енергії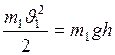 , (2.1.6)
, (2.1.6) (див. рис. 2.1.2), або
(див. рис. 2.1.2), або  .
. і
і 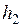 . Кінетичні енергії куль відразу після удару дорівнюватимуть потенціальним енергіям в точках, які відповідають кутам відхилення
. Кінетичні енергії куль відразу після удару дорівнюватимуть потенціальним енергіям в точках, які відповідають кутам відхилення  і
і  .
.
 , (2.1.7)
, (2.1.7) , (2.1.8)
, (2.1.8) ,
,  .
. .
.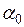 ,
,  :
: ,
,
 .
.
 ;
; 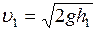 ;
;  .
. .
.
 рухається після удару в початковому напрямку, а знак мінус – у протилежному.
рухається після удару в початковому напрямку, а знак мінус – у протилежному. і абсолютно непружного (2.1.4) удару. Дані занесіть у протокол дослідів.
і абсолютно непружного (2.1.4) удару. Дані занесіть у протокол дослідів.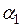 , град.
, град.

 , яка підвішена на нитці довжиною
, яка підвішена на нитці довжиною  , відхиляють на кут
, відхиляють на кут  від вертикалі й відпускають. Потім кут відхилення змінюють на
від вертикалі й відпускають. Потім кут відхилення змінюють на  й повторюють дослід. Знайти відношення максимальних швидкостей кульки в першому і другому випадках.
й повторюють дослід. Знайти відношення максимальних швидкостей кульки в першому і другому випадках. .
. , а кінетична енергія відрізняється вдвічі
, а кінетична енергія відрізняється вдвічі  . Знайти відношення мас
. Знайти відношення мас  .
. .
. однакові. Порівняйте їх імпульси.
однакові. Порівняйте їх імпульси.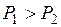 .
.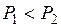 .
. .
. .
. .
. .
. , а кінетичні енергії рівні
, а кінетичні енергії рівні  .
. інша куля, маса якої в
інша куля, маса якої в  разів більша за масу нерухомої кулі. Знайти відношення швидкості кулі, що налітає, після абсолютно пружного удару до її початкової швидкості.
разів більша за масу нерухомої кулі. Знайти відношення швидкості кулі, що налітає, після абсолютно пружного удару до її початкової швидкості. .
.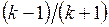 .
. . Удар абсолютно непружний. Потім проводиться аналогічний дослід ІІ з однаковими непружними кулями
. Удар абсолютно непружний. Потім проводиться аналогічний дослід ІІ з однаковими непружними кулями  . Знайти відношення коефіцієнтів ефективного відновлення
. Знайти відношення коефіцієнтів ефективного відновлення  .
. .
. .
. .
. кг рухається зі швидкістю
кг рухається зі швидкістю  м/с і ударяється об нерухоме тіло такої ж маси. Вважаючи удар центральним і абсолютно непружним, визначити кількість теплоти, що виділилася під час удару.
м/с і ударяється об нерухоме тіло такої ж маси. Вважаючи удар центральним і абсолютно непружним, визначити кількість теплоти, що виділилася під час удару. кг і
кг і 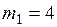 кг рухаються назустріч одна одній зі швидкостями
кг рухаються назустріч одна одній зі швидкостями  м/с і
м/с і  м/с, спрямованими уздовж однієї прямої. З якою швидкістю вони будуть рухатися після абсолютно непружного удару?
м/с, спрямованими уздовж однієї прямої. З якою швидкістю вони будуть рухатися після абсолютно непружного удару? . Під час поступального ходу тягарця
. Під час поступального ходу тягарця  ,
,
 – алгебраїчна сума моментів сил, що діють на тіло відносно осі обертання;
– алгебраїчна сума моментів сил, що діють на тіло відносно осі обертання;  – момент інерції тіла відносно тієї ж осі;
– момент інерції тіла відносно тієї ж осі;  (
( – сила натягу,
– сила натягу,  – плече цієї сили, рівне радіусу шківа) і моменту сили тертя
– плече цієї сили, рівне радіусу шківа) і моменту сили тертя  .
. , де
, де  – момент інерції системи без тягарців (для кожного маятника відомий),
– момент інерції системи без тягарців (для кожного маятника відомий),  – число тягарців
– число тягарців  .
.
 Тягарець
Тягарець  ,
, . (2.2.3)
. (2.2.3)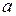 можна знайти з досліду. Нитка намотується на шків, тягарець
можна знайти з досліду. Нитка намотується на шків, тягарець  розраховується прискорення:
розраховується прискорення: .
. збігається з прискоренням
збігається з прискоренням  .
.
 .
.
 , де
, де 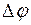 – зміна кута повороту шківа.
– зміна кута повороту шківа. ,
, ,
, .
. . (2.2.6)
. (2.2.6) . (2.2.7)
. (2.2.7)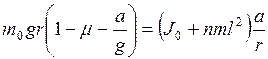 .
.
 , с
, с

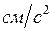

 ;
;  ;
;  ;
;  ;
; 
 ? Для того, щоб вибрати тягарець потрібно навести курсор миші на нього і натиснути ліву кнопку миші.
? Для того, щоб вибрати тягарець потрібно навести курсор миші на нього і натиснути ліву кнопку миші. .
. .
.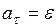 .
. і
і 
 . Моменти сил рівні
. Моменти сил рівні  . Порівняти плечі сил
. Порівняти плечі сил  і
і  .
. .
. .
. і
і 
 , намотані нитки, до кінців яких прикріплені тягарці однакової маси. Порівняти прискорення опускання тягарців. Вважати маси шківів рівними. Тертям знехтувати.
, намотані нитки, до кінців яких прикріплені тягарці однакової маси. Порівняти прискорення опускання тягарців. Вважати маси шківів рівними. Тертям знехтувати. .
. .
. .
. обертів, зупинився. Робота сил гальмування
обертів, зупинився. Робота сил гальмування  Дж. Визначити момент сил гальмування.
Дж. Визначити момент сил гальмування.
 .
.
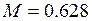

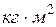 , обертається із частотою
, обертається із частотою  об/хв. Після припинення дії на нього обертального моменту маховик зупинився під дією тертя в підшипниках через час
об/хв. Після припинення дії на нього обертального моменту маховик зупинився під дією тертя в підшипниках через час  хв. Вважаючи тертя в підшипниках постійним, визначити момент сил тертя М.
хв. Вважаючи тертя в підшипниках постійним, визначити момент сил тертя М.


 кг котиться без ковзання по горизонтальній поверхні зі швидкістю
кг котиться без ковзання по горизонтальній поверхні зі швидкістю  м/с. Знайти повну кінетичну енергію кулі.
м/с. Знайти повну кінетичну енергію кулі. , де
, де  – кут повороту,
– кут повороту,  диска відомі. Знайти закон, за яким змінюється момент сил, що діють на маховик.
диска відомі. Знайти закон, за яким змінюється момент сил, що діють на маховик. .
. .
. .
. см, маса
см, маса  г. Визначити момент інерції диска відносно осі, що проходить через середину одного з радіусів перпендикулярно до площини диска.
г. Визначити момент інерції диска відносно осі, що проходить через середину одного з радіусів перпендикулярно до площини диска.


 .
. .
. .
. см, дорівнює
см, дорівнює  . Знайти радіус вала. Вал має форму циліндра.
. Знайти радіус вала. Вал має форму циліндра.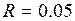 м.
м. м.
м.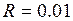 м.
м. м. На вал намотаний шнур, до кінця якого прив’язаний тягарець
м. На вал намотаний шнур, до кінця якого прив’язаний тягарець  кг. Тягарець опускається за час
кг. Тягарець опускається за час  с з висоти
с з висоти  м, а потім підіймається на висоту
м, а потім підіймається на висоту  . Визначити момент інерції махового колеса.
. Визначити момент інерції махового колеса.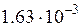


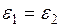 .
. .
.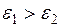 .
.


