
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Захист від радіоактивних випромінюваньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
КОНТРОЛЬНІ ЗАПИТАННЯ
1. Типи радіоактивних джерел, джерела радіаційного фону і їх величина. 2. Яка проникна здатність випромінювань різного типу? 3. Які методи захисту від 4. Пояснити принцип вимірювання потужності експозиційної дози випромінювання різними приладами.
ЛАБОРАТОРНА РОБОТА №1.27
ЗАХИСТ ВІД РАДІОАКТИВНИХ ВИПРОМІНЮВАНЬ Мета роботи: з’ясування впливу зовнішнього та внутрішнього опромінення на живий організм і вимірювання інтенсивності радіоактивних випромінювань. Прилади: радіометр-дозиметр гамма-бета-випромінювань РКС-01.
ТЕОРЕТИЧІ ВІДОМОСТІ Джерела радіоактивних випромінювань можна поділити на природні та штучні, космічні та земні, відкриті та закриті тощо. Розрізняють квантове ( З точки зору дії радіації на живий організм важливим є поділ джерел на закриті (тверді, рідкі та газоподібні препарати, ізольовані від навколишнього середовища герметичною оболонкою) і відкриті. Перші призводять до зовнішнього опромінення, а другі – через органи дихання і травлення – можуть потрапляти всередину організму і спричиняють внутрішнє опромінення, один із наслідків якого – тривалість дії в разі накопичення радіоактивних ізотопів у різних органах людини. Радіоактивне випромінювання, діючи на живий організм, призводить безпосередньо (для потоків заряджених часток) або опосередковано (тобто електронами і ядрами, що одержали енергію відповідно від квантового потоку або потоку нейтронів) до іонізації молекул і атомів його тканин. Вільні електрони та іони, що утворюються в результаті такої іонізації, беруть участь у різних хімічних реакціях з утворенням надзвичайно активних вільних і нових молекул, які через ланцюжок ще не вивчених до кінця реакцій можуть викликати модифікацію важливих у біологічному відношенні молекул, тобто призвести до утворення невластивих живому організму молекул. Усі описані вище процеси відбуваються за дуже короткий час ≈1 мкс. Потім через секунди або десятиліття можуть відбуватися біохімічні зміни в організмі, що є безпосередньою причиною біологічних ефектів: загибелі клітин або їх аномального розвитку (злоякісні пухлини, зміна генетичного коду тощо). Вплив радіації на живий організм зазвичай залежить від величини іонізації (переданої тканинам енергії) в організмі і типу органів, у яких відбулася іонізація (коефіцієнт чутливості Оскільки опромінюється тією чи іншою мірою все живе на Землі, то для оцінки шкідливого впливу на здоров’я людини введена так звана гранично допустима доза (ГДД) для людей категорії А (особи, що працюють з радіоактивними джерелами), і границя дози (ГрД) для осіб категорії Б та В. У випадку зовнішнього рівномірного опромінення всього тіла значення ГДД не повинно перевищувати за 1 рік 50 мЗв, а ГрД – 5 мЗв. Величина ГДД Для характеристики радіаційної небезпеки перебування людини в різних місцях (робоче місце в лабораторії, на підприємстві, вдома і т. ін.) зручно користуватись потужністю поглинутої дози, що вимірюється в Гр/с; Гр/рік і т. п., і розраховувати допустимий час Безпека людини вимагає вжиття певних заходів, щодо запобігання проникненню радіонуклідів усередину організму: закриті джерела точкового типу слід зберігати в контейнерах, робочі місця обладнати поглинаючими екранами тощо.
ДОЗИМЕТРИЧНІ ПРИЛАДИ Дозиметричними називають прилади, призначені для виявлення і оцінки густини потоку радіації та вимірювання потужності експозиційної дози рентгенівського і
ПОРЯДОК ВИКОНАННЯ РОБОТИ 1. Виміряти дозиметром потужність експозиційної дози природного радіоактивного випромінювання (це випромінювання називається фоном 2. Перевірити роботу сигналізатора перевищення потужності дози випромінювання, порівнюючи поріг сигналізації з виміряною дозиметром потужністю експозиційної дози в тому ж місці. 3. За виміряними значеннями
4. Визначити можливий ступінь променевої хвороби для кількох значень часу перебування і товщини свинцевого захисту від
за таблицею, що знаходиться в лабораторії, для роботи протягом одного заняття і одного семестру. КОНТРОЛЬНІ ЗАПИТАННЯ 1. Механізм дії радіоактивних випромінювань на людину, гранично допустимі дози для різних категорій населення. 2. Одиниці вимірювання ГД, ЕД, потужності ГД і експозиційної дози, співвідношення між одиницями. 3. Типи радіоактивних джерел, джерела радіаційного фону і його величина. 4. Яка проникна здатність випромінювань різного типу? 5. Які методи захисту від 6. Пояснити процес вимірювання потужності експозиційної дози випромінювання різними приладами. 7. Визначити допустимий час перебування людини у відомому полі радіоактивного випромінювання, визначити ГД і ЕД.
ЛАБОРАТОРНА РОБОТА №1.28
ТЕОРЕТИЧНІ ВІДОМОСТІ Похідна за часом основного закону радіоактивного розпаду
визначає зміну з часом активності А зразка
де
Для визначення  згідно з (1.28.2) зручно побудувати залежність згідно з (1.28.2) зручно побудувати залежність  , оскільки величина активності пропорційна швидкості рахунку , оскільки величина активності пропорційна швидкості рахунку  досліджуваного зразка досліджуваного зразка
Із графіка залежності
Природна радіоактивність атмосферного повітря визначається вмістом у ґрунті радію (
ПОРЯДОК ВИКОНАННЯ РОБОТИ 1. Установити чистий аерозольний фільтр у гніздо пилососа, увімкнути одночасно установку РКС-01 для вимірювання фону
Таблиця 1.28.1
2. Записати в таблицю значення
КОНТРОЛЬНІ ЗАПИТАННЯ 1. Види радіоактивного випромінювання. 2. Основний закон радіоактивного розпаду. 3. Походження природної радіоактивності повітря. 4. Що називається активністю препарату? 5. Що називається періодом піврозпаду ізотопів? 6. Схема розпаду радію. 7. Як визначити період піврозпаду короткоживучих ізотопів? 8. Як визначити питому активність атмосферного повітря?
ІІ. ВІРТУАЛЬНІ ЛАБОРАТОРНІ РОБОТИ
І МЕТОДИКА ВИМІРЮВАНЬ
На стійкій підставці закріплена вертикальна труба (1) з підвісами для куль (2) (рис. 2.1.1). Одна з куль (масою Виразимо енергетичний коефіцієнт відновлення через кути відхилення куль до і після удару. Припустимо, що кулю масою
де Після удару кулі розходяться, піднімаючись на висоту
Підставивши (2.1.6) - (2.1.8) у (2.1.3), одержимо
Знаючи вираз для
де Враховуючи, що
З формул (2.1.6) - (2.1.8) випливає, що
Залежність
Знак плюс в правій частині (2.1.11) відповідає випадку, коли куля
ПОРЯДОК ВИКОНАННЯ РОБОТИ
У роботі ставляться дві задачі: 1. Визначення енергетичного коефіцієнта відновлення для різних пар куль, що стикаються. 2. Перевірка закону збереження імпульсу при ударі.
Проведіть досліди щодо зіткнення різних пар куль. У кожному досліді виміряйте кути відхилення
Таблиця 2.1.1
Запитання, що часто виникають. 1. Як провести дослід? Спочатку треба вибрати кулі, які будуть стикатися. Далі треба відхилити праву кулю на довільний кут (цей кут потрібно запам’ятати) і відпустити кулю. Після того як кулі зупиняться, потрібно занести експериментальні дані в протокол дослідів і обчислити шукані величини. 2. Як вибрати кулю? Для зміни кулі потрібно навести курсор миші на кулю, яка знаходиться в коробці і натиснути ліву кнопку миші. Кулю з лівого боку вибирають з лівої коробки, з правого – з правої. 3. Як відхилити кулю на довільний кут? Для того, щоб відхилити кулю, закріплену до підвісу, слід навести на неї курсор миші, натиснути ліву кнопку миші, і, утримуючи її, відхилити кулю на довільний кут. Кут зручно заміряти за нижньою шкалою.
КОНТРОЛЬНІ ЗАПИТАННЯ
До експерименту
1. Кульку масою · 1. · · 2. 2. Імпульси двох тіл однакові · 1. · · 2. 3. Кінетичні енергії тіл з масами · · · 4. Імпульси тіл з масами · · · 5. Імпульси двох тіл відрізняються у два рази · 2. · 1. · 4. 6. Чи може тіло мати енергію, не маючи імпульсу? · Так. · Ні. · Немає однозначної відповіді. 7. Для якого зіткнення справедливий закон збереження механічної енергії? · Для абсолютно пружного. · Для абсолютно непружного. · Для кожного. 8. Чи може тіло мати імпульс і не мати при цьому енергії? · Так. · Ні. · Немає однозначної відповіді. 9. Для якого зіткнення коефіцієнт енергетичного відновлення · Для абсолютно пружного. · Для абсолютно непружного. · Для кожного. 10. Для якого зіткнення виконується закон збереження імпульсу? · Для абсолютно пружного. · Для абсолютно непружного. · Для кожного. Після експерименту
1. На нерухому кулю налітає зі швидкістю · · · 2. Дві більярдних кулі з однаковими масами, що рухаються назустріч одна одній, зазнають абсолютно пружного зіткнення. Швидкість першої кулі до зіткнення 2 м/с, другої 3 м/с. Знайти швидкість першої кулі після зіткнення. · 3 м/с. · 1 м/с. · 5 м/с. 3. Дві кулі масами 1.5 кг і1.0 кг рухаються в одній площині зі швидкістю 2 м/с і 4 м/с, відповідно. Вектори швидкостей куль утворюють · 2 м/с. · 3 м/с. · 0.25 м/с. 4. Які закони використовуються для виведення робочих формул цієї лабораторної роботи? · Закони Ньютона, закон збереження імпульсу. · Закони Ньютона, закони збереження енергії. · Закони збереження імпульсу і енергії. 5. У досліді І куля масою · 1/3. · 2. · 1/2. 6. Куля масою · · · 7. Тіло масою · 3 Дж. · 6 Дж. · Немає вірної відповіді. 8. Частинка 1 абсолютно пружно зіткнулася з частинкою 2, яка не рухалась до удару. Знайти відношення мас частинок · 1. · 3. · Немає вірної відповіді. 9. Дві непружніх кулі з масами · 6 м/с. · 3.6 м/с. · Немає вірної відповіді. 10. Чи може коефіцієнт енергетичного відновлення · Не може. · Так, якщо удар абсолютно непружний. · Так, якщо удар абсолютно пружний.
ЛАБОРАТОРНА РОБОТА №2.2
Мета роботи: перевірити основний закон динаміки обертального руху за допомогою маятника Обербека.
Маятник Обербека складається зі шківа і стрижнів, закріплених на одній нерухомій горизонтальній осі, що проходить через центр симетрії системи. Відносно цієї осі маятник може обертатися. На стрижні насаджені однакові за масою тягарці
ТЕОРЕТИЧНІ ВІДОМОСТІ Основний закон динаміки твердого тіла, що обертається навколо нерухомої осі, має вигляд:
де Маятник Обербека обертається під дією моменту сили натягу нитки Момент інерції маятника дорівнює Рівняння (2.2.1) перепишемо у вигляді:
звідси
Прискорення
Якщо нитка пересувається по шківу без проковзування, то тангенціальне прискорення точок на поверхні шківа Тому кутове прискорення маятника
Момент сили тертя визначаємо із закону збереження енергії. Тягарець
З іншого боку
де N – кількість обертів шківа. Враховуючи це, перепишемо (2.2.5):
звідси:
Позначимо
Тоді
Підставивши (2.2.3), (2.2.4), (2.2.7) в (2.2.2), одержимо
ПОРЯДОК ВИКОНАННЯ РОБОТИ Виберіть тягарець Таблиця 2.2.1
Запитання, що часто виникають. 1. Як вибрати тягарець 2. Як змінити положення тягарців на маятнику? Положення тягарців на маятнику змінюється шляхом натиснення лівої кнопки миші.
КОНТРОЛЬНІ ЗАПИТАННЯ До експерименту
1. Що відбудеться з моментом інерції маятника Обербека, якщо тягарець масою · Збільшиться. · Зменшиться. · Не зміниться. 2. Які сили створюють обертальний момент маятника Обербека? · Сила ваги і сила тертя. · Сила ваги і натягу нитки. · Сила натягу нитки і сила тертя. 3. Який зміст має величина · Момент інерції тягарця масою · Момент інерції маятника Обербека без тягарців. · Момент інерції шківа. 4. Точка обертається по колу радіусом · · · 5. Який закон перевіряється за допомогою маятника Обербека? · Закон збереження імпульсу. · Основний закон динаміки обертального руху. · ІІ закон Ньютона. 6. На тіло, здатне обертатися навколо нерухомої осі, діють дві сили · · · 7. Як зміниться кутове прискорення маятника Обербека в разі зміни найвіддаленішого від осі обертання положення вантажів · Збільшиться. · Зменшиться. · Залишається без зміни. 8. Які величини вимірюють в експерименті з маятником Обербека для визначення прискорення · Довжина нитки · Радіус шківа · Маса тягарця 9. Які припущення про фізичні властивості нитки зроблені в цій роботі? · Довжина нитки набагато більша за радіус шківа. · Маса нитки порівнянна з масою тягарця · Можна знехтувати розтягом нитки і її масою. 10. Який закон використовується в роботі для визначення моменту сили тертя? · Закон збереження енергії. · ІІ закон Ньютона. · Закон збереження моменту імпульсу. Після експерименту 1. На шківи, що мають форму дис
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 526; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.253.224 (0.011 с.) |

 -,
-,  -,
-, 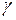 - і нейтронного випромінювання точкового джерела і паралельного потоку цих часток?
- і нейтронного випромінювання точкового джерела і паралельного потоку цих часток? різних органів людини до радіації може відрізнятися на порядок). Крім того, у випадку зовнішнього опромінення різні типи випромінювання проникають на різну глибину, тобто мають різну проникну здатність.
різних органів людини до радіації може відрізнятися на порядок). Крім того, у випадку зовнішнього опромінення різні типи випромінювання проникають на різну глибину, тобто мають різну проникну здатність. 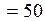 мЗв гарантовано (на сучасному рівні) не викликає змін в організмі в разі рівномірного 50-літнього опромінення. Якщо людина одержала більшу ЕД можливі різні захворювання, наприклад, променева хвороба різного ступеня: 1-го – 1-2 Зв, 2-го – 2-4 Зв, 3-го – 4-6 Зв і 4-го – більше 6 Зв (для 3-го та 4-го ступенів ймовірність смерті понад 50%).
мЗв гарантовано (на сучасному рівні) не викликає змін в організмі в разі рівномірного 50-літнього опромінення. Якщо людина одержала більшу ЕД можливі різні захворювання, наприклад, променева хвороба різного ступеня: 1-го – 1-2 Зв, 2-го – 2-4 Зв, 3-го – 4-6 Зв і 4-го – більше 6 Зв (для 3-го та 4-го ступенів ймовірність смерті понад 50%). перебування в даному місці. Однак дозиметричні прилади переважно проградуйовані для квантового випромінювання в позасистемних одиницях потужності експозиційної дози - Зв/с; Р/год тощо (1 Р – 1 Рентген – експозиційна доза фотонного випромінювання, що створює в 1
перебування в даному місці. Однак дозиметричні прилади переважно проградуйовані для квантового випромінювання в позасистемних одиницях потужності експозиційної дози - Зв/с; Р/год тощо (1 Р – 1 Рентген – експозиційна доза фотонного випромінювання, що створює в 1  повітря за нормальних умов
повітря за нормальних умов  пар іонів і відповідає поглинутій біологічним об’єктом дозі
пар іонів і відповідає поглинутій біологічним об’єктом дозі 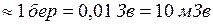 ).
).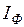 ) у лабораторії і поза приміщенням, а також на заданій відстані
) у лабораторії і поза приміщенням, а також на заданій відстані  від декількох радіоактивних препаратів
від декількох радіоактивних препаратів 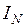 .
.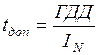 .
.

 ,
,
 і
і  – число радіоактивних ядер в початковий
– число радіоактивних ядер в початковий 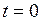 і розглядуваний
і розглядуваний  момент часу. Знаходження залежності
момент часу. Знаходження залежності  ƒ(t) дає можливість для короткоживучих ізотопів (період піврозпаду не повинен перевищувати кількох десятків годин) безпосередньо за швидкістю зменшення активності препарату з часом
ƒ(t) дає можливість для короткоживучих ізотопів (період піврозпаду не повинен перевищувати кількох десятків годин) безпосередньо за швидкістю зменшення активності препарату з часом  визначити постійну розпаду
визначити постійну розпаду 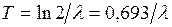 .
.

 .
.
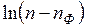 від t визначається кутовий коефіцієнт рівняння (1.28.4), який дорівнює
від t визначається кутовий коефіцієнт рівняння (1.28.4), який дорівнює  .
.
 на 1 г ґрунту), продукти розпаду якого потрапляють в атмосферу. Концентрація радону в повітрі відповідає питомій активності
на 1 г ґрунту), продукти розпаду якого потрапляють в атмосферу. Концентрація радону в повітрі відповідає питомій активності  . Продукти розпаду радону є металами (рис. 1.28.1) і осідають на поверхні твердих часток диму, пилу, туману (загальна назва – золі), які концентрує аерозольний фільтр під час прокачування через нього повітря.
. Продукти розпаду радону є металами (рис. 1.28.1) і осідають на поверхні твердих часток диму, пилу, туману (загальна назва – золі), які концентрує аерозольний фільтр під час прокачування через нього повітря. і прокачувати повітря 5 – 10 хв. Потім помістити фільтр у гніздо приладу РКС-01 і виміряти залежність швидкості рахунку
і прокачувати повітря 5 – 10 хв. Потім помістити фільтр у гніздо приладу РКС-01 і виміряти залежність швидкості рахунку  від часу
від часу 
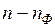
 .
.
 ) знаходиться в стані спокою (
) знаходиться в стані спокою ( ), а інша (масою
), а інша (масою  ) – відхиляється на довільний кут. За шкалою (3) відраховуються кути відхилення куль у градусах.
) – відхиляється на довільний кут. За шкалою (3) відраховуються кути відхилення куль у градусах. над початковим рівнем відліку потенціальної енергії (0), потім відпускають. Безпосередньо перед ударом куля має швидкість
над початковим рівнем відліку потенціальної енергії (0), потім відпускають. Безпосередньо перед ударом куля має швидкість  .
. Згідно з законом збереження механічної енергії
Згідно з законом збереження механічної енергії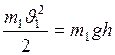 , (2.1.6)
, (2.1.6) (див. рис. 2.1.2), або
(див. рис. 2.1.2), або  .
. і
і 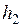 . Кінетичні енергії куль відразу після удару дорівнюватимуть потенціальним енергіям в точках, які відповідають кутам відхилення
. Кінетичні енергії куль відразу після удару дорівнюватимуть потенціальним енергіям в точках, які відповідають кутам відхилення  і
і  .
.
 , (2.1.7)
, (2.1.7) , (2.1.8)
, (2.1.8) ,
,  .
. .
.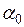 ,
,  :
: ,
,
 .
.
 ;
; 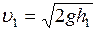 ;
;  .
. .
.
 рухається після удару в початковому напрямку, а знак мінус – у протилежному.
рухається після удару в початковому напрямку, а знак мінус – у протилежному. і абсолютно непружного (2.1.4) удару. Дані занесіть у протокол дослідів.
і абсолютно непружного (2.1.4) удару. Дані занесіть у протокол дослідів.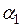 , град.
, град.

 , яка підвішена на нитці довжиною
, яка підвішена на нитці довжиною  , відхиляють на кут
, відхиляють на кут  від вертикалі й відпускають. Потім кут відхилення змінюють на
від вертикалі й відпускають. Потім кут відхилення змінюють на  й повторюють дослід. Знайти відношення максимальних швидкостей кульки в першому і другому випадках.
й повторюють дослід. Знайти відношення максимальних швидкостей кульки в першому і другому випадках. .
. , а кінетична енергія відрізняється вдвічі
, а кінетична енергія відрізняється вдвічі  . Знайти відношення мас
. Знайти відношення мас  .
. .
. однакові. Порівняйте їх імпульси.
однакові. Порівняйте їх імпульси.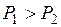 .
.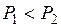 .
. .
. .
. .
. .
. , а кінетичні енергії рівні
, а кінетичні енергії рівні  .
. інша куля, маса якої в
інша куля, маса якої в  разів більша за масу нерухомої кулі. Знайти відношення швидкості кулі, що налітає, після абсолютно пружного удару до її початкової швидкості.
разів більша за масу нерухомої кулі. Знайти відношення швидкості кулі, що налітає, після абсолютно пружного удару до її початкової швидкості. .
.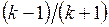 .
. . Удар абсолютно непружний. Потім проводиться аналогічний дослід ІІ з однаковими непружними кулями
. Удар абсолютно непружний. Потім проводиться аналогічний дослід ІІ з однаковими непружними кулями  . Знайти відношення коефіцієнтів ефективного відновлення
. Знайти відношення коефіцієнтів ефективного відновлення  .
. .
. .
. .
. кг рухається зі швидкістю
кг рухається зі швидкістю  м/с і ударяється об нерухоме тіло такої ж маси. Вважаючи удар центральним і абсолютно непружним, визначити кількість теплоти, що виділилася під час удару.
м/с і ударяється об нерухоме тіло такої ж маси. Вважаючи удар центральним і абсолютно непружним, визначити кількість теплоти, що виділилася під час удару. кг і
кг і 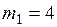 кг рухаються назустріч одна одній зі швидкостями
кг рухаються назустріч одна одній зі швидкостями  м/с і
м/с і  м/с, спрямованими уздовж однієї прямої. З якою швидкістю вони будуть рухатися після абсолютно непружного удару?
м/с, спрямованими уздовж однієї прямої. З якою швидкістю вони будуть рухатися після абсолютно непружного удару? . Під час поступального ходу тягарця
. Під час поступального ходу тягарця  ,
,
 – алгебраїчна сума моментів сил, що діють на тіло відносно осі обертання;
– алгебраїчна сума моментів сил, що діють на тіло відносно осі обертання;  – момент інерції тіла відносно тієї ж осі;
– момент інерції тіла відносно тієї ж осі;  (
( – сила натягу,
– сила натягу,  – плече цієї сили, рівне радіусу шківа) і моменту сили тертя
– плече цієї сили, рівне радіусу шківа) і моменту сили тертя  .
. , де
, де  – момент інерції системи без тягарців (для кожного маятника відомий),
– момент інерції системи без тягарців (для кожного маятника відомий),  .
.
 Тягарець
Тягарець  ,
, . (2.2.3)
. (2.2.3)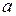 можна знайти з досліду. Нитка намотується на шків, тягарець
можна знайти з досліду. Нитка намотується на шків, тягарець  розраховується прискорення:
розраховується прискорення: .
. збігається з прискоренням
збігається з прискоренням  .
.
 .
.
 , де
, де 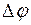 – зміна кута повороту шківа.
– зміна кута повороту шківа. ,
, ,
, .
. . (2.2.6)
. (2.2.6) . (2.2.7)
. (2.2.7)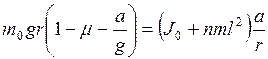 .
.

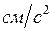

 ;
;  ;
;  ;
;  ;
; 
 ? Для того, щоб вибрати тягарець потрібно навести курсор миші на нього і натиснути ліву кнопку миші.
? Для того, щоб вибрати тягарець потрібно навести курсор миші на нього і натиснути ліву кнопку миші. .
. .
.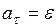 .
. і
і 
 . Моменти сил рівні
. Моменти сил рівні  . Порівняти плечі сил
. Порівняти плечі сил  і
і  .
. .
. .
.


