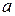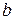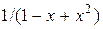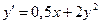Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По специальности 1-31 03 06-01 «Экономическая кибернетикаСодержание книги
Поиск на нашем сайте
П Р О Г Р А М М А Государственного экзамена По специальности 1-31 03 06-01 «Экономическая кибернетика (математические методы и компьютерное моделирование В экономике)»
Программа утверждена Советом математического факультета Протокол № 7 от “ 26 “ января 2012 г.
Декан математического факультета ___________ С.П.ЖОГАЛЬ
Гомель 2012 На государственном экзамене выпускник должен продемонстрировать умение систематизировать информационные сведения программы экзамена, знание основных теорем и понятий, понимание взаимосвязей между ними, умение ими пользоваться. С учетом этих требований экзаменующийся по каждому вопросу билета должен сделать обзор материала, соответствующего формулировке вопросов, сопровождая ответ доказательством отдельных теорем и утверждений.
Математический анализ
1. Числа натуральные, рациональные и действительные. Полнота множества действительных чисел. 2. Последовательности и их сходимость (сходящиеся последовательности в топологическом пространстве; сходящиеся последовательности действительных чисел; теорема о существовании предела монотонной ограниченной последовательности; свойства последовательностей действительных чисел, связанные с арифметическими операциями над последовательностями). 3. Числовые ряды (сходимость числовых рядов; сходимость рядов с неотрицательными членами, признаки их сходимости; абсолютно сходящиеся ряды, их свойства; условно сходящиеся ряды). 4. Производная функции в точке. Дифференциал. Производные и дифференциалы высших порядков. 5. Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа и Коши. Формула Тейлора. 6. Непрерывные функции. Свойства функций, непрерывных на отрезке. 7. Интеграл Римана (определение, существование, свойства; дифференцируемость интеграла Римана по верхнему пределу). Существование первообразной у непрерывной функции. Формула Ньютона-Лейбница. 8. Дифференцируемость функций нескольких переменных (частные производные и дифференциалы функций многих переменных; необходимые условия дифференцируемости функций многих переменных; достаточные условия дифференцируемости). 9. Формула Тейлора для функций нескольких переменных. Достаточные условия локального экстремума.
10. Производные и дифференциалы высших порядков функции многих переменных. Необходимые и достаточные условия экстремума функции многих переменных. 11. Равномерная сходимость функциональных последовательностей и рядов (критерий Коши равномерной сходимости функциональных последовательностей и рядов; признак Вейерштрасса равномерной сходимости функционального ряда). 12. Двойной интеграл Римана (сведение двойного интеграла к повторному; замена переменных в двойном интеграле; кратные интегралы).
Дифференциальные уравнения 1. Понятие дифференциального уравнения и его решения. Интегрируемые типы дифференциальных уравнений.
2. Линейные дифференциальные уравнения произвольного порядка. Общее решение линейного неоднородного дифференциального уравнения. 3. Общее решение линейного однородного дифференциального уравнения. 4. Метод вариации произвольных постоянных. 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Дифференциальные уравнения с частными Производными 1. Классификация уравнений в частных производных. 2. Метод Фурье на примере решения смешанной задачи для уравнения колебаний струны. Дискретная математика 1. Булевы функции. Элементарные булевы функции. Теорема о числе булевых функций. 2. Минимизация булевых функций. Алгоритм построения минимальной дизъюнктивной нормальной формы.
Геометрия и алгебра 1. Комплексные числа, операции над ними. Формула Муавра. Корни из комплексного числа. 2. Многочлены с действительными коэффициентами. Теорема Безу. Основная теорема алгебры. 3. Теоремы Крамера, Кронекера - Капелли. 4. Квадратичные формы. Матрицы линейных преобразований и их свойства. 5. Теорема о разложении вектора по двум неколлинеарным векторам. Необходимое и достаточное условие линейной зависимости 3-х векторов. 6. Прямая на плоскости. Общее уравнение прямой. Теорема о задании прямой в аффинной системе координат линейным уравнением. Матричный анализ 1. Псевдообратная матрица. Нормальное псевдорешение системы линейных уравнений. 2. Жорданова нормальная форма. Алгоритм нахождения жордановой нормальной формы.
3. Функция от матрицы. Интерполяционный многочлен Лагранжа-Сильвестра. 4. Нормы векторов и матриц. Наиболее употребительные нормы матриц. Теория вероятностей и математическая статистика 1. Аксиомы теории вероятностей. Классическое определение вероятности. Свойства вероятности. 2. Условная вероятность. Независимость событий. Формулы полной вероятности и Байеса. Схема Бернулли. 3. Функция распределения, ряд распределения, плотность распределения вероятности, их свойства. Закон распределения случайной величины. 4. Выборка, эмпирическая функция распределения, гистограмма относительных частот. Несмещенные, состоятельные и эффективные оценки. 5. Проверка статистических гипотез. Критерии согласия. Критерий согласия Пирсона. 6. Случайный процесс, определение, состояния, реализации случайного процесса. Конечномерные распределения. Классификация случайных процессов: гауссовские случайные процессы, процессы с независимыми приращениями, процессы с некоррелированными приращениями, стационарные процессы, марковские процессы.
Методы численного анализа 1. Интерполирование функций (постановка задачи; единственность интерполяционного многочлена; формула Лагранжа). 2. Численное интегрирование (квадратурные формулы трапеций и Симпсона; погрешность). 3. Одношаговые методы решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка.
ЭВМ и программирование 1. Язык программирования Паскаль. Стандартные типы данных. Выражения, операнды, операции. Простейший ввод/вывод. Процедуры ввода/вывода. Управляющие операторы. 2. Язык программирования Паскаль. Типы данных, определяемые пользователем. Синтаксис определения типов, описания переменных. Работа с переменными объявленных типов. 3. Язык программирования Паскаль. Текстовые, типизированные и нетипизированные файлы и работа с ними. 4. Язык программирования С. Динамическая память. Указатели и работа с ними. 5. Язык программирования С. Указатели и массивы. Обработка символьных величин. 6. Язык программирования С++. Понятие и описание классов. Конструкторы и деструкторы классов: назначение, виды и порядок вызова. Создание и уничтожение экземпляров классов. 7. Язык программирования С++. Наследование классов. Управление доступом к членам класса при наследовании. Множественное наследование, виртуальные базовые классы.
Математическая теория финансового риска 1. Риск. Понятие портфеля рисков. Страхование рисков. Типы страховых портфелей. Определения и характеристики простейшего, простого и реального страхового портфелей. 2. Краткосрочное страхование жизни. Страховая премия. Нетто-премия. Принцип эквивалентности страховых обязательств. Защитная надбавка. 3. Модели краткосрочного страхования жизни. Модель индивидуальных потерь. Вероятность разорения. Применение нормального приближения в моделях краткосрочного страхования жизни. Математическая экономика 1. Отношение предпочтения, его свойства. Функция полезности, ее свойства. Теорема Дебре. Функция полезности производственного потребления, ее свойства. Предельная полезность. Закон Госсена. 2. Задачи оптимального потребления. Оптимальное поведение потребителя в неоклассическом случае и при ограниченном запасе товаров. Геометрическая интерпретация решения задачи потребления в случае двух товаров.
3. Три типа решений задач потребления. Функции спроса, их свойства. Предельная полезность добавочного дохода. Кривые «бюджет-потребление» и «цена-потребление». Уравнение Слуцкого. Теорема Слуцкого. Методы оптимизации 1. Симплекс-метод. Алгоритм обратной матрицы. 2. Обобщенное и классическое правила Лагранжа для задач с ограничениями в виде равенств. 3. Условие Эйлера для основной задачи вариационного исчисления. Исследование операций 1. Задача о коммивояжере. Метод ветвей и границ 2. Матричные игры. Верхняя и нижняя цены игры. Основная теорема. 3. Модели сетевого планирования. Расчет временных параметров. Компьютерные сети 1. Процессы взаимодействия устройств в сети. Модель взаимодействия открытых систем ISO/OSI и стандартные стеки коммуникационных протоколов. 2. Классификация сетей. Требования, предъявляемые к современным вычислительным сетям. Подходы к обеспечению пользователей по доступу к разделяемым ресурсам сети. Избранные главы информатики 1. Методы работы с массивами (Array) в языке Ruby. 2. Методы работы с хэшами (Hash) в языке Ruby.
Модели данных и СУБД 1. Основные модели баз данных. Понятие системы управления базами данных. Этапы проектирования баз данных. Нормализация отношений. 2. Использование языка SQL для выборки данных из таблиц. 3. Использование языка SQL для обновления, вставки, удаления строк таблиц.
Эконометрика 1. Множественная линейная регрессионная модель, проверка адекватности модели (предпосылки Гаусса-Маркова, метод наименьших квадратов, оценка значимости коэффициентов регрессии, оценка значимости коэффициента детерминации). 2. Нарушение предпосылок классической линейной регрессии: мультиколлинеарность, гетероскедастичность (критерии Голдферда-Квандта, Уайта), автокорреляция (автокорреляционная функция, частная автокорреляционная функция, критрерий Дарбина-Уотсона). 3. Фиктивные переменные в регрессионных моделях (фиктивные переменные сдвига, фиктивные переменные наклона). 4. Анализ временных рядов: составляющие временного ряда, тест Чоу на наличие тренда, выделение сезонной компоненты временного ряда (сезонные индексы, сезонные фиктивные переменные, одномерный анализ Фурье). Экономика предприятия 1. Оплата труда в Республике Беларусь: формы, системы, государственное регулирование. 2. Производственная программа предприятия: содержание, показатели и порядок формирования в современных условиях.
3. Себестоимость продукции: сущность, виды, показатели, методика их расчета и пути снижения. 4. Кадры предприятия: состав, структура, показатели оценки и пути повышения эффективности использования. 5. Основные средства предприятия: состав, структура, методы оценки, показатели и пути повышения эффективности использования. ЛИТЕРАТУРА Математический анализ 1. Никольский С.М. Курс математического анализа: Учеб.пособие в 2-х томах, 3-е издание. М., Наука, 1983. 2. Кудрявцев Л.Д. Курс математического анализа: Учебник в 2-х т. М. Высш.школа. 1981. 3. Зорич В.А. Математический анализ: Учебник в 2-х т. М.: Наука, 1981, 1984. 4. Рудин У. Основы математического анализа. М.: Мир, 1976. 319 с.
Геометрия и алгебра 1. Милованов М.В., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия. – Мн.: Амалфея, 2001 г. 2. Монахов В.С., Бузланов А.В. Алгебра и теория чисел: Практикум: учебное пособие. В 2-х частях. Ч.1. – Мн.: Изд. центр БГУ, 2007 г. 3. Виноградов И.М. Основы теории чисел. – М.: Наука, 1972 г. 4. Дубровин Б.А., Новиков С.П., Фоменко А.Г. Современная геометрия. – М.: Наука, 1979 г.
Дифференциальные уравнения 1. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. Минск: Вышэйшая школа, 1974. 2. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М.: 1984.
Дискретная математика 1. Яблонский С.В. Введение в дискретную математику. – М.: Наука, 1979. 2. Гаврилов Г.П. Сборник задач по дискретной математике. – М.: Наука, 1977.
Методы оптимизации 1. Габасов Р., Кириллова Ф.М. Методы оптимизации. Минск,1981. Исследование операций 1. Вагнер Г. Основы исследования операций. Т. 1-3 М.: Сов. радио, 1972 - 1973. 2. Вентцель Е.С. Исследование операций. М.: Сов. радио, 1972. Методы численного анализа 1. Березин, И.С. Методы вычислений: в 2 т. Т.1, 2. / И.С.Березин, Н.П.Жидков. – М.: Наука, 1966. – 630с. 2. Демидович, Б.П. Численные метода анализа / Б.П. Демидович, И.А. Марон, Э.З. Шувалова. – М.: Наука, 1967. – 368с. 3. Копчёнова, Н.В. Вычислительная математика в примерах и задачах / Н.В. Копчёнова, И.А. Марон. – М.: Наука, 1972. – 368с.
ЭВМ и программирование 1. Бородич, Ю. С. Паскаль для персональных компьютеров: справ. пособие / Ю. С. Бородич, А. Н. Вальвачев, А. И. Кузьмич – Мн.: Выш. шк.: БФ ГИТМП “НИКА”, 1991. – 365 с. 2. Вальвачев, А. Н. Программирование на языке Паскаль для персональных ЭВМ ЕС: справ. пособие / А. Н. Вальвачев, В. С. Крисевич – Мн.: Выш. шк., 1989. – 223 с. 3. Зуев Е. А. Программирование на языке TURBO PASCAL 6.0, 7.0 / Е. А. Зуев. – М.: Радио и связь, 1993. – 384 с. 4. Турбо Паскаль 7.0. – К.: Торгово-издательское бюро BHV, 1996. – 448с. 5. Фаронов, В. В. Turbo Pascal 7.0. Начальный курс: учебное пособие / В. В. Фаронов. – М.: «Нолидж», 1997. – 616 с. 6. Касаткин А.И., Вальвачев А.Н. Профессиональное программирование на языке Си: От Turbo C к Borland C++: Справ. Пособие: Под общ. Ред. А.И. Касаткина. – Мн.: Выш. шк., 1992. – 240 с.: ил. 7. Касаткин, А.И. Профессиональное программирование на языке Си. Управление ресурсами: Справ. пособие / А.И. Касаткин. – Мн.: Выш. шк., 1992. – 432 с.: ил. 8. Демидович, Е.М. Основы алгоритмизации и программирования. Язык СИ.: учеб. пособие / Е.М. Демидович. – СПб.:БХВ-Петербург, 2006. – 440 с.
9. Подбельский, В.В. Язык С++: учебное пособие / В.В. Подбельский. – М.: Финансы и статистика, 1995. – 560 с. 10. С/С++. Программирование на языке высокого уровня / Т.А. Павловская. – СПб.: Питер, 2002. – 464с.: ил. 11. Юлин, В.А. Приглашение к СИ./ В.А. Юлин, И.Р. Булатова – Мн.: Выш. шк., 1990. – 224 с.: ил. 12. Березин, Б.И. Начальный курс М и С++ / Б.И. Березин, С.Б. Березин. М.:ДИАЛОГ-МИФИ, 2001. – 288 с.
Математическая экономика 1. Альсевич, В. В. Математическая экономика. Конструктивная теория: учеб. пособие / В. В. Альсевич. – Мн.: Дизайн ПРО, 1998. – 240 с. 2. Альсевич, В. В. Введение в математическую экономику. Конструктивная теория: учеб. пособие / В. В. Альсевич. – М.: Изд-во ЛКИ, 2005. 3. Альсевич, В. В. Введение в математическую экономику. Конструктивная теория: учеб. пособие. Изд. второе, испр. / В. В. Альсевич. – М.: Изд-во ЛКИ, 2007. – 256 с. 4. Ашманов, С. А. Введение в математическую экономику: учеб. пособие / С. А. Ашманов. – М.: Наука, 1984. – 296 с. 5. Интрилигатор, М. Математические методы оптимизации и экономическая теория / М. Интрилигатор. – М.: Айрис-пресс, 2002. 6. Колемаев, В. А. Математическая экономика / В. А. Колемаев. – М.: ЮНИТИ, 1998. Избранные главы информатики 1. Орлов, С. А. Технологии разработки программного обеспечения: Учебник для вузов. 3-е изд. / С. А. Орлов. — СПб.: Питер, 2004. 2. Буч, Г. Язык UML. Руководство пользователя / Грейди Буч, Джеймс Рамбо, Айвар Джекобсон. – М.: ДМК Пресс, 2004.
Модели данных и СУБД 1. Горев, А. Эффективная работа с СУБД / А. Горев, Р. Ахаян, С. Макашарипов. – СПб.: Питер, 1997. - 704с. 2. Грабер, М. Введение в SQL / М. Грабер - М.: Издательство "Лори", 1996. – 382с. 3. Змитрович, А.И. Базы данных: учебное пособие для вузов / А.И. Змитрович. – Мн.: Университетское, 1991.-271с. 4. Моррисон, Дж. Базы данных. Проектирование, реализация и сопровождение. Теория и практика / Дж. Моррисон, А. Ухтомский, М. Пере. – СПб.: Издательский дом «Вильямс», 2001. – 1120с. 5. Боуман, Д. Практическое руководство по SQL / Д. Боуман, С. Эмерсон, М. Дарновски. – СПб.: Издательский дом «Вильямс», 2001. – 352с. 6. Дейт К. Введение в системы баз данных //6-издание. - Киев: Диалектика, 1998. - 784 с. Математическая теория финансового риска 1. Медведев, Г.А. Математические модели финансовых рисков. Риски страхования. / Г.А. Медведев / Ч. 2. Мн.: БГУ. – 2001. – 278 с. 2. Ротарь, В.И. Введение в математическую теорию страхования. / В.И. Ротарь, В.Е. Бенинг/ Обозрение прикладной и промышленной математики. 1994. – Т.1. – вып. 5. – С. 698 – 779. 3. Gerber H. An Introduction to Mathematical Risk Theory. Homewood: Irwin Inc. – 1979. – 285 c. Эконометрика 1. Елисеева, И.И. Эконометрика: учебное пособие / И.И.Елисеева.- М.: Финансы и статистика, 2004. 2. Харин, Ю.С. Эконометрическое моделирование: учебное пособие / В.И.Харин [.и др.]. – Мн.: БГУ, 2003. Экономика предприятия 1. Трудовой кодекс Республики Беларусь: одобрен Советом Республики 30 июня 1999г. (в ред.закона Республики Беларусь от 24 декабря 2007г., № 299-3) // Национальный реестр правовых актов Республики Беларусь. – 2008. – № 3, 2/1396. 2. Основные положения по составу затрат, включаемых в себестоимость продукции (работ, услуг): Постановление Минэкономики, Минфина, Минстатистики и анализа, Минтруда от 4.07.2002г., № 142/95/60/95. 3. Единая тарифная сетка работников производственных отраслей экономики Республики Беларусь. – Мн., 2000. 4. Головачев, А.С. Экономика предприятия: учебное пособие / А.С. Головачев. – Мн. – в 2-х ч., ч.1 – 2007г., ч.2 – 2008г. 5. Экономика предприятия (фирмы): учебное пособие / под ред. О.И. Волкова, О.В. Девяткина. – 3-е изд., перераб. и доп. – М., 2007. 6. Экономика предприятия: учебное пособие / под общ. ред. А.И.Ильина. – 3-е изд., перераб. и доп. – Мн., 2005. 7. Бабук, И.М. Экономика предприятия / И.М.Бабук. – Мн.,2006. 8. Экономика предприятия: учебное пособие / под общ. ред. Л.Н. Нехорошевой. – Мн., 2005. 9. Экономика, организация и планировании е промышленного производства: учебное пособие / под общ. ред. Т.В.Карпей. – 4-е изд., испр. и доп. – Мн., 2004. ПЕРЕЧЕНЬ ЗАДАЧ Математический анализ
1. Найти предел
2. Является ли функция
3. Проведя исследование, построить график функции
4. Вычислить следующий интеграл:
5. Найти
6. Вычислить
7. Найти площадь фигуры, ограниченной кривыми y = 2 x - x 2, x + y = 0.
8. Найти:
9. Исследовать на сходимость
10. Исследовать ряд на сходимость
11. Исследовать на сходимость
12. Написать ряд Фурье функции
13. Найти области сходимости функционального ряда и его сумму и исследовать ее на непрерывность
14. Найти
15. Найти дифференциал d 3 u, если u = x 3 + y 3 + xy (x - y)
16. Изменить порядок интегрирования в следующих повторных интегралах
17. Вычислить а) ОА - отрезок прямой линии; б) ОА - парабола, ось которой есть OY; в) ОА - ломаная линия, состоящая из отрезков ОВ, оси ОХ и отрезка ВА, параллельного оси OY.
18. Применяя формулу Грина вычислить следующий криволинейный интеграл
19. Вычислить предел:
20. Существуют ли такие a и b, при которых функция
всюду дифференцируема?
Геометрия и алгебра 1. Найти
2. Решите матричные уравнения, т.е. найдите множества матриц X, для которых справедливо равенство
3. Пользуясь схемой Горнера, вычислите f (б), если: f (x) = x4 – 3x3 + 6x6 – 10x = 16, б = 4; 4. Найдите разложение вектора с по векторам a и b: а (4, – 2), b (3,5), c (1, – 7);
5. Докажите, что фигура, ограниченная прямыми x– 3y + 1 = 0, x – 3y + 12 = 0, 3x + y – 1 = 0, 3x + y + 10 = 0, – квадрат. Вычислите его площадь.
6. Найдите точку, симметричную точке P (6, – 5, 5) относительно плоскости 2x – 3y + z – 4 = 0.
7. Исследуйте, являются ли данные векторы 1, sin x, cos x линейно зависимыми. В случае утвердительного ответа найдите нетривиальную линейную комбинацию, равную 0:
8. Исследуйте на совместность и найдите решения системы:
9. Найдите фундаментальную систему решений системы уравнений:
10. Линейный оператор f в базисе е 1, е 2 имеет матрицу
11. Убедитесь, что векторы а 1, а 2 ортогональны, и дополните систему а 1, а 2 до ортогонального базиса, если:
а 1 (1, – 2, 2, – 3), а 2 (2, – 3, 2, 4)
12. Найдите расстояние между параллельными плоскостями:
13. Найдите проекцию точки
14. Найдите базис ядра линейного оператора А Матричный анализ 1. Найти жорданову нормальную форму матрицы:
а)
2. Вычислить функцию от матрицы:
а)
в) 3. Найти евклидову, октаэдрическую и кубическую нормы от следующих матриц: а)
Дифференциальные уравнения 1. Проинтегрировать следующие системы дифференциальных уравнений:
2. Проинтегрировать следующую систему дифференциальных уравнений:
3. Найти решение указанной ниже задачи:
4. Найти решение указанной ниже задачи:
5. Найти решение указанной ниже задачи:
6. Найти решение указанной ниже задачи:
7. Найти решение указанной ниже задачи:
8. Найти решение указанной ниже задачи:
9. Проинтегрировать следующее уравнение:
Методы оптимизации 1. Решить симплекс-методом
2. Исследовать задачу НЛП, используя правило множителей Лагранжа
z = x1+2x22 ® min 6x1 + x2 £ 4
3. Построить оптимальную по суммарному штрафу последовательность обслуживания заявок на одном приборе с данными
Исследование операций 1. Решить задачу о кратчайшем маршруте
2. Решить матричную игру геометрическим способом
Эконометрика 1. По статистическим данным об объемах продаж (
Построить уравнение линейной множественной регрессии и оценить его качество.
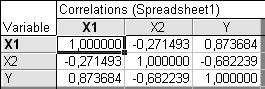
2. По статистическим данным бюджетного обследования пяти случайно выбранных семей приведен корреляционно-регрессионный анализ в ППП STATIATICA. Результаты анализа представлены на рисунке
Оценить регрессионную зависимость накоплений от дохода и имущества семьи. 3. Для двух видов продукции А, В модели зависимости удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
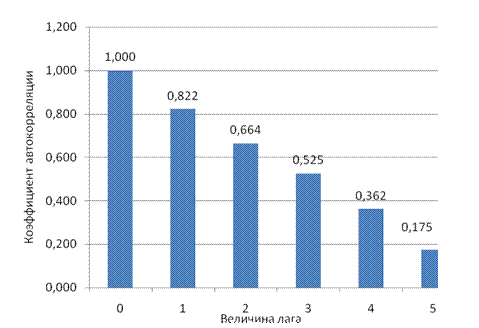
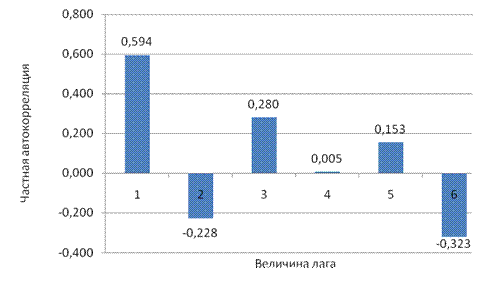
Определите коэффициенты эластичности по каждому виду продукции и поясните их смысл. 4. Имеются данные о ежемесячных объемах выпуска продукции (тыс. штук) предприятия. На рисунке представлены графики автокорреляционной (АКФ) и частной автокорреляционной (ЧАКФ) функций.
График АКФ
График ЧАКФ Провести анализ структуры временного ряда.
5. Для двух видов продукции А, В модели зависимости удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом: Определите коэффициенты эластичности по каждому виду продукции и поясните их смысл.
Методы численного анализа 1. Используя первую интерполяционную формулу Ньютона для равноотстоящих узлов вычислить приближённое значение функции в точке х*. х* = 1,25
2. Вычислить интеграл по обобщенной формуле трапеций, разбив отрезок интегрирования на 4 равные части.
3. Применяя метод Эйлера, решить задачу Коши на отрезке [0,1], разбив его на 4 равные части.
Избранные главы информатики 1. В численном массиве найти сумму отрицательных элементов. 2. Найти все индексы, по которым располагается максимальный элемент. 3. Найти все элементы, большие среднего арифметического элементов. 4. Дан произвольный хэш с числовыми ключами. Необходимо удалить те пары, ключ которых нечётный. 5. Дан хэш. Необходимо получить массив, содержащий сначала ключи хэша, а затем значения хэша. 6. Дано два хэша, значения которых - целые числа. Выполнить их слияние таким образом, чтобы для совпадающих ключей бралось максимальное значение.
П Р О Г Р А М М А Государственного экзамена по специальности 1-31 03 06-01 «Экономическая кибернетика (математические методы и компьютерное моделирование В экономике)»
Программа утверждена Советом математического факультета Протокол № 7 от “ 26 “ января 2012 г.
Декан математического факультета ___________ С.П.ЖОГАЛЬ
Гомель 2012 На государственном экзамене выпускник должен продемонстрировать умение систематизировать информационные сведения программы экзамена, знание основных теорем и понятий, понимание взаимосвязей между ними, умение ими пользоваться. С учетом этих требований экзаменующийся по каждому вопросу билета должен сделать обзор материала, соответствующего формулировке вопросов, сопровождая ответ доказательством отдельных теорем и утверждений.
Математический анализ
1. Числа натуральные, рациональные и действительные. Полнота множества действительных чисел. 2. Последовательности и их сходимость (сходящиеся последовательности в топологическом пространстве; сходящиеся последовательности действительных чисел; теорема о существовании предела монотонной ограниченной последовательности; свойства последовательностей действительных чисел, связанные с арифметическими операциями над последовательностями). 3. Числовые ряды (сходимость числовых рядов; сходимость рядов с неотрицательными членами, признаки их сходимости; абсолютно сходящиеся ряды, их свойства; условно сходящиеся ряды). 4. Производная функции в точке. Дифференциал. Производные и дифференциалы высших порядков. 5. Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа и Коши. Формула Тейлора. 6. Непрерывные функции. Свойства функций, непрерывных на отрезке. 7. Интеграл Римана (определение, существование, свойства; дифференцируемость интеграла Римана по верхнему пределу). Существование первообразной у непрерывной функции. Формула Ньютона-Лейбница. 8. Дифференцируемость функций нескольких переменных (частные производные и дифференциалы функций многих переменных; необходимые условия дифференцируемости функций многих переменных; достаточные условия дифференцируемости). 9. Формула Тейлора для функций нескольких переменных. Достаточные условия локального экстремума. 10. Производные и дифференциалы высших порядков функции многих переменных. Необходимые и достаточные условия экстремума функции многих переменных. 11. Равномерная сходимость функциональных последовательностей и рядов (критерий Коши равномерной сходимости функциональных последовательностей и рядов; признак Вейерштрасса равномерной сходимости функционального ряда). 12. Двойной интеграл Римана (сведение двойного интеграла к повторному; замена переменных в двойном интеграле; кратные интегралы).
Дифференциальные уравнения 1. Понятие дифференциального уравнения и его решения. Интегрируемые типы дифференциальных уравнений.
2. Линейные дифференциальные уравнения произвольного порядка. Общее решение линейного неоднородного дифференциального уравнения. 3. Общее решение линейного однородного дифференциального уравнения. 4. Метод вариации произвольных постоянных. 5. Линейные дифференциальные уравнения с постоянными коэффициентами.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.245.123 (0.016 с.) |

 .
.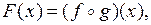
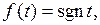
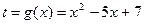 непрерывной на
непрерывной на 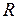 ? Дифференцируемой на
? Дифференцируемой на 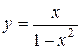 .
.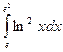 .
.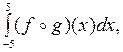 где
где 
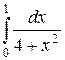 .
.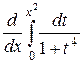 .
.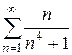 .
. .
.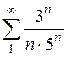 .
.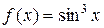 на отрезке
на отрезке 

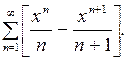
 , если
, если 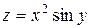 .
.
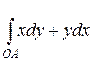 , где 0 начало координат и точка A (1,1)по следующим кривым:
, где 0 начало координат и точка A (1,1)по следующим кривым: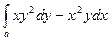 , где
, где  - окружность x 2 + y 2 = 1.
- окружность x 2 + y 2 = 1. .
.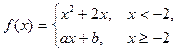
 ;
; x
x 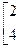
 =
= 
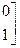 x;
x;
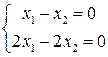
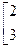
 . Найдите его матрицу в базисе а 1= 2 е 1- е 2, а 2 = е 1+ 2 е 2.
. Найдите его матрицу в базисе а 1= 2 е 1- е 2, а 2 = е 1+ 2 е 2.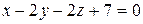 и
и 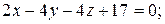

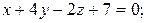
 пространства
пространства 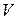 , заданного в некотором базисе матрицей А:
, заданного в некотором базисе матрицей А: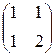
 ; б)
; б) 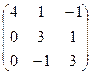 ; в)
; в) 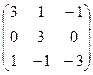 ;
;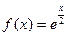 , где A =
, где A = 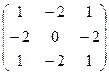 ; б)
; б) 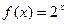 , где A =
, где A = 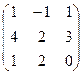 ;
;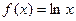 , гдеA =
, гдеA = 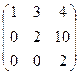
 ; б)
; б) 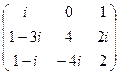 ; в)
; в) 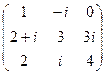 ;
;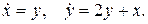


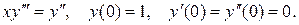
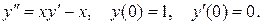
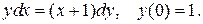
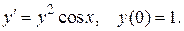


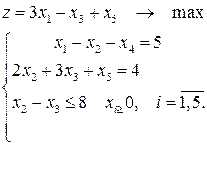

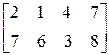
 ), затратах на рекламу одной фирмы (
), затратах на рекламу одной фирмы ( ) и индексе потребительских расходов за ряд текущих лет (
) и индексе потребительских расходов за ряд текущих лет (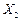 ) проведен регрессионный анализ в MS Excel. Результаты анализа представлены на рисунке.
) проведен регрессионный анализ в MS Excel. Результаты анализа представлены на рисунке.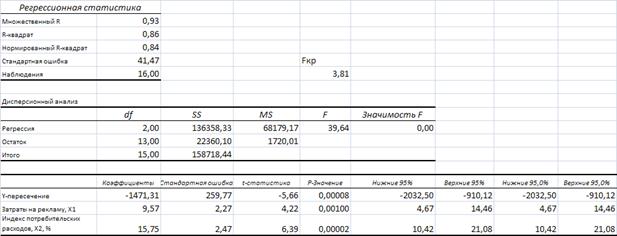

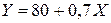 ,
, 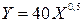 .
.
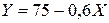 ,
, 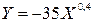 .
.