
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6. Индексный метод в статистических исследованияхСодержание книги
Поиск на нашем сайте
Вопросы 1. Понятие об индексах. Классификация общих индексов. 2. Индивидуальные и общие индексы. Агрегатная форма как основная форма общего индекса. [ 1, с. 143–178; 2, с. 526-552; 3, с. 81–92; 5, с. 439–478]
Методические указания к теме Наиболее распространенными статистическими показателями являются индексы. Индекс представляет собой относительную величину, полученную в результате сопоставления уровней сложных социально-экономических показателей во времени, в пространстве и по сравнению с планом. Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс (обозначается символом i, у которого проставляется символ соответствующей индексируемой величины). Он характеризует изменение одного элемента совокупности. Например, индивидуальный индекс цены на отдельный вид продукции (товара) рассчитываются по формуле:
где р – цена за единицу продукции. Подстрочное обозначение «0» и «1» соответствуют уровню базисного и отчётного периода времени. Изменение совокупностей, состоящих из несопоставимых элементов (например, различных видов продукции), изучают с помощью групповых или общих индексов (I). Последние по методам построения подразделяются на агрегатные индексы и средневзвешенные из индивидуальных индексов. Ниже приводятся формулы агрегатных индексов: 1) физического объёма (количества продукции, товара):
где g – индексированная величина (количество); p0 – соизмеритель (цена продукции, товара), который фиксируется на уровне одного и того же периода. Разница между числителем и знаменателем индекса означает абсолютное изменение (прирост «+» или снижение «–») результативного показателя за счет изменения индексируемой величины: В данном случае – изменение товарооборота за счет изменения физического объема (количества):
2) цен (или других качественных показателей):
где объём g – объём (количество) являются весами, взятые на одинаковом отчётном уровне. Разница между числителями и знаменателями индекса означает абсолютное изменение товарооборота (выручки от продаж) в результате среднего изменения цен или экономического (продаж) денежных средств населения в результате среднего снижения (повышения) цен:
3) товарооборота (выручка от реализации или продаж):
Разница между числителями и знаменателями индекса Между общими агрегатными индексами, а также абсолютными изменениями результативного показателя существует взаимосвязь:
Аналогичным образом составляются формулы индексов других социально-экономических показателей. При этом в теории статистики разработана определённая символика и применяются соответствующие условные обозначения. Помимо рассмотренных ранее обозначений количества продукции (g) и цены за единицу продукции (p) применяются символы: z – себестоимость единицы продукции; zq – денежные затраты на выпуск продукции.
Контрольные вопросы 1. Какие виды индексов рассчитываются в практике статистики? 2. В чем заключается основное правило при построении общего индекса агрегатной формы? 3. В чем отличие агрегатных индексов от индексов средних гармонических и арифметических? 4. Поясните экономическую сущность разницы числителя и знаменателя индексов цен, физического объема и товарооборота? 5. Как взаимосвязаны цепные и базисные индексы?
7. Задания для самостоятельной работы
В процессе изучения дисциплин «Общая теория статистики», «Статистика» студенты очной и заочной форм обучения в рамках часов самостоятельной работы выполняют письменные индивидуальные задания, которые должны отвечать следующим требованиям: 1. Выполненное задание предоставляется на проверку после последнего практического занятия, на котором разбирается решение данного типа задач. 2. В начале работы указывается соответствующий номер варианта. 3. Задачи необходимо располагать в том же порядке, в каком они даны в задании. Перед решением задачи должно быть полностью приведено ее условие. 4. Решение задачи должно сопровождаться необходимыми формулами, развернутыми расчетами и краткими пояснениями. Задачи, к которым даны ответы без развернутых расчетов, пояснений и кратких выводов, будут считаться нерешенными. Решение задач следует по возможности оформлять в виде таблиц. 5. Все расчеты относительных показателей нужно производить с принятой в статистике точностью до 0,001, а проценты – до 0,1. 6. Выполненная работа должна быть оформлена аккуратно, написана разборчиво, чисто, без помарок и зачеркиваний. Запрещается произвольно сокращать слова (допускаются лишь общепринятые сокращения). Таблицы надо оформлять в соответствии с правилами, принятыми в статистике. Страницы работы должны быть пронумерованы и иметь достаточно широкие поля для замечаний рецензента. 7. При правильном выполнении каждое задание оценивается отдельно отметкой «зачтено». 8. К зачету допускаются студенты отметку «зачтено» по большинству решаемых задач (четыре и более). Если студент не может самостоятельно выполнить индивидуальную работу или какую-то ее часть, следует обратиться к преподавателю за консультацией в установленные графиком дни. Целью самостоятельной работы является закрепление теоретических знаний, полученных студентами на занятиях и в процессе работы с литературой по следующим темам: 1. Статистическая сводка. Группировка. Таблицы. 2. Статистические показатели. 3. Средние величины. 4. Статистическое изучение вариации. 5. Выборочный метод в статистике. 6. Статистическое изучение динамики социально-экономических явлений. 7. Индексный метод в статистических исследованиях. 8. Графический метод изучения статистических данных. Задания к самостоятельной индивидуальной работе составлены в 6 вариантах. Выбор варианта зависит от начальной буквы фамилии студента представлен в табл. 7.1: Таблица 7.1 Соответствие варианта фамилии студента
При написании индивидуальной работы, прежде всего, рекомендуется ознакомиться с соответствующими разделами программы данного курса, методическими указаниями, разработанными кафедрой по отдельным темам, а также изучить рекомендуемую литературу, при этом уделив особое внимание методам построения статистических показателей и их анализу. Каждый вариант самостоятельной работы из 7 задач по наиболее важным темам раздела «Общая теория статистики». Задача 1 составлена на тему «Статистическая сводка, метод группировок». При решении этой задачи необходимо понять суть аналитической группировки и установить характер взаимосвязи между факторным и результативным признаками. При этом следует иметь в виду, что в основу группировки берется факторный признак. В задаче 2 необходимо правильно использовать формулу средней арифметической или средней гармонической величины. При решении задачи 3 следует изучить значение моды и медианы – разновидностей средних величин. Значение моды и медианы нужно также определить и графически: моду – при помощи построения гистограммы, медиану – при помощи построения кумуляты. Для решения задачи 4 необходимо изучить темы «Средние величины и показатели вариации». По данным интервального вариационного ряда распределения необходимо исчислить среднюю дисперсию, среднее квадратическое отклонение обычным способом или способом моментов. При исчислении показателей способом моментов необходимо правильно понять момент первого и второго порядка. Задача 5 составлена по теме «Выборочное наблюдение». Для расчета ошибок репрезентативности нужно изучить тему «Выборочное наблюдение», понять значение генеральной и выборочной совокупности, способы отбора и варианты формирования выборки: бесповторный и повторный. Задача 6 составлена на тему «Динамические ряды» – на расчет и усвоение аналитических показателей динамических рядов, либо на применение методов их анализа. Задача 7 составлена на тему «Индексы». При решении задачи могут применяться взаимосвязанные общие агрегатные индексы, их взаимосвязь, а также взаимосвязь абсолютных приростов обобщающего индексируемого показателя. 7.1 Задания для самостоятельной работы для варианта I Задача 1. Имеются данные по предприятиям легкой промышленности.
Таблица 7.1.1 Данные для построения групповой таблицы
Для выявления зависимости между основными средствами и объемом произведенной продукции предприятий произвести группировку предприятий по их основным средствам, образовав 4 группы с равными интервалами. По каждой группе и в целом по всей совокупности предприятий рассчитать: 1. Число предприятий. 2. Основные средства всего и в среднем на одно предприятие. 3. Объем произведенной продукции всего и в среднем на одно предприятие. Результаты представить в виде итоговой аналитической таблицы. Сделать выводы. Задача 2. Имеются данные о среднегодовом товарообороте продавцов трех торговых предприятий за 2 смежных месяца отчетного года.
Таблица 7.1.2 Данные для исчисления средних показателей
Вычислить: 1. Средний дневной оборот продавца по трем предприятиям: а) за июнь; б) за июль. 2. Указать вид применяемых средних величин. Задача 3. В результате обследования получены следующие данные о распределении студентов-заочников учебного заведения по возрасту.
Таблица 7.1.3 Данные для исчисления структурных средних величин
Определить: 1. Моду среднего возраста студентов-заочников: а) по формуле; б) с помощью построения гистограммы. 2. Дать пояснение значению моды. Задача 4. По данным таблицы 7.1.3 рассчитать: 1. Способом «моментов»: а) средний возраст студентов-заочников; б) дисперсию. 2. Коэффициент вариации. Сделать вывод о типичности средней величины.
Задача 5. На основании 20 % выборки, проведенного по способу бесповторного отбора, получено следующие распределение рабочих по стажу работы. Таблица 7.1.4 Данные распределения рабочих по стажу работы
Определить границы, в которых находится доля рабочих, имеющих стаж работы от 5 до 15 лет в генеральной совокупности, при t = 2. Задача 6. С целью выявления основной тенденции производства хлопчатобумажных тканей за 2008–2013 гг. произвести аналитическое выравнивание динамического ряда, используя уравнение прямой линии. Таблица 7.1.5 Данные для расчета теоретических уровней
Эмпирические и теоретические уровни нанести на один общий график. Сделать выводы.
Задача 7. Имеются данные о производстве продукции двумя компаниями за два месяца. Таблица 7.1.6 Данные для исчисления индексов
Определить общие индексы затрат предприятия, себестоимости, физического объема выпуска продукции.
7.2 Задания для самостоятельной работы для варианта II Задача 1. Имеются данные об уставном капитале и работающих активах коммерческих банков. Таблица 7.21 Данные для построения групповой таблицы, млн руб.
Для выявления зависимости между уставным капиталом и работающими активами коммерческих банков произвести группировку коммерческих банков по их уставному капиталу, образовав 4 группы с равными интервалами. По каждой группе и по всей совокупности банков подсчитать: 1. Число банков. 2. Уставный капитал всего и в среднем на один банк. 3. Работающие активы всего и в среднем на один банк. Результаты представить в виде итоговой аналитической таблицы. Сделать выводы. Задача 2. Имеются данные о работе трех предприятий акционерного общества за два месяца. Таблица 7.2.2 Данные для исчисления средних показателей
Рассчитать: 1. Средний процент реализации прогноза в феврале и марте, указать виды средних. 2. Абсолютные и относительные отклонения фактического объема реализации от планового в феврале и марте.
Задача 3. Результаты социологического обследования клиентов одного из крупных банков выявили следующий их основной состав.
Таблица 7.2.3 Данные для исчисления структурных средних
Определить: 1. Медиану среднего возраста клиентов: а) по формуле; б) с помощью построения кумуляты. 2. Дать пояснение значению медианы.
Задача 4. Анализы молока по проценту содержания сухих веществ показали следующие распределения: Таблица 7.2.4 Данные для исчисления показателей вариации
Вычислить: дисперсию, среднее квадратичное отклонение, коэффициент вариации. Задача 5. Методом случайного бесповторного отбора было проведено пятипроцентное выборочное обследование возраста служащих расчетно-кассового центра республики с общим числом служащих 4050 человек. В результате обследования были получены следующие результаты: средний возраст служащих 36,6 лет при среднем квадратическом отклонении 9,5 лет. Определить с вероятностью 0,997 пределы, в которых находится средний возраст служащих.
Задача 6. По данным баланса Банка России средства в иностранной валют, размещенные у нерезидентов, в отчетном году, составляли млрд. руб. (данные условные). Таблица 7.2.5 Данные для исчисления показателей динамики
Определить: 1. Средний уровень ряда динамики. 2. Базисные и цепные абсолютные приросты 3. Базисные и цепные темпы роста и прироста. 4. Средний абсолютный прирост, средний темп роста и прироста. Указать вид средних, применяемых в расчетах. Сделать выводы. Задача 7. Имеются данные о средних ценах на продукты по двум рынкам города за два периода. Таблица 7.2.6 Данные для исчисления индексов
Вычислить общие индексы товарооборота, цен, физического объема продаж. Определить в отчетном периоде прирост товарооборота и разложить по факторам (за счет изменения цен и объема продажи товаров). Показать взаимосвязь индексов. Сделать выводы. 7.3 Задания для самостоятельной работы для варианта III Задача 1. Имеются данные об уставном капитале и капитале двадцати коммерческих банков. Таблица 7.3.1 Данные для построения групповой таблицы, млн руб.
Для выявления зависимости между уставным капиталом и капиталом банков произвести группировку коммерческих банков по их уставному капиталу, образовав 4 группы с равными интервалами. По каждой группе и в целом по всей совокупности банков подсчитать: 1. Число банков. 2. Уставный капитал всего и в среднем на один банк. 3. Капитал всего и в среднем на один банк. Результаты представить в виде итоговой аналитической таблицы. Сделать выводы. Задача 2. Имеются следующие данные о заработной плате и численности работающих по двум предприятиям отрасли. Таблица 7.3.2 Данные для исчисления средних показателей
1. Вычислить среднюю заработную плату работающих по двум предприятиям: а) за базисный период; б) за отчетный период; 2. Указать вид применяемых средних. Задача 3. Следующие данные характеризуют возрастную структуру сотрудников предприятия. Таблица 7.3.3 Данные для исчисления структурных средних
Определить: 1. Моду возраста сотрудников предприятия: а) по формуле; б) с помощью построения гистограммы. 2. Дать пояснение значению моды. Задача 4. По исходным данным определить показатели вариации. Таблица 7.3.4 Данные для исчисления показателей вариации
1. Способом «моментов»: а) средний процент сахаристости продукции; б) средний квадрат отклонений (дисперсию). 2. Коэффициент вариации.
Задача 5. Учитывая данные задачи 4, которые представляют собой 10 % выборочное обследование продукции, определить с вероятностью 0,997 возможные пределы, в которых находится средний процент сахаристости продукции во всей партии товара.
Задача 6. С целью выявления основной тенденции продаж стиральных машин в области за 2008–2013 годы, произвести аналитическое выравнивание динамического ряда, используя уравнение прямой линии. Таблица 7.3.5 Данные для нахождения теоретических уровней
Эмпирические и теоретические уровни нанести на один общий график. Задача 7. Динамика цены продукции и количества проданной продукции характеризуется следующими данными. Таблица 7.3.6 Данные для исчисления индексов
Определить общие индексы выручки, цен, физического объема продаж. Показать взаимосвязь между исчисленными индексами. Рассчитать изменение в отчетном периоде выручки от продаж продукции и разложить по факторам (за счет изменения цены и количества проданной продукции).
7.4 Задания для самостоятельной работы для варианта IV Задача 1. Имеются данные о совокупном денежном доходе за месяц и размере семьи (данные условные). Таблица 7.4.1 Данные для построения групповой таблицы
Для выявления зависимости между размером семьи и объемом совокупного денежного дохода произвести группировку семей по их размеру, образовав 2 группы с равными интервалами. По каждой группе семей и в целом по всей совокупности семей рассчитать: 1. Число семей. 2. Численность членов семей всего и в среднем на одну семью. 3. Совокупный денежный доход всего и в среднем на одну семью. Результаты представить в виде итоговой аналитической таблицы. Сделать выводы.
Задача 2. Имеются данные об объеме реализации продукции по двум продовольственным магазинам за два квартала. Таблица 7.4.2 Данные для исчисления средних показателей
Вычислить: 1. Среднюю цену продукта по двум магазинам: а) за II квартал; б) за III квартал; в) за два квартала вместе. 2. Указать вид применяемых средних величин.
Задача 3. Имеются следующие данные о выпуске однородной продукции предприятиями отрасли. Таблица 7.4.3 Данные для исчисления структурных средних величин
Определить: 1. Медиану объема выпуска продукции: а) по формуле; б) с помощью построения кумуляты. 2. Дать пояснение значению медианы.
Задача 4. По данным табл. 7.4.3 рассчитать показатели вариации: а) размах; б) среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; д) коэффициент вариации. Сделать вывод о типичности средней величины.
Задача 5. По данным задач 3 и 4 вычислить средний объем выпускаемой продукции во всей генеральной совокупности предприятий, состоящей из 1500 предприятий. Расчеты провести с вероятностью 0,954.
Задача 6. Имеются следующие данные о численности населения города по состоянию на 1 января каждого года: Таблица 7.4.4 Данные для исчисления показателей динамики
Для анализа динамики численности населения города вычислить: 1. Абсолютные приросты, темпы роста и темпы прироста по годам и к 1997 году. 2. Среднегодовую численность населения. 3. Среднегодовой абсолютный прирост. 4. Среднегодовой темп роста и темп прироста. Сделать выводы. Задача 7. Динамика себестоимости и объема производства продукции характеризуется следующими данными: Таблица 7.4.5 Данные для исчисления индексов
Определить: а) общий индекс затрат на производство; б) общий индекс себестоимости продукции; в) общий индекс физического объема производства продукции. Определить в отчетном периоде изменение суммы затрат на производство продукции и разложить по факторам (за счет изменения себестоимости и объема выработанной продукции). Показать взаимосвязь между исчисленными индексами.
7.5 Задания для самостоятельной работы для варианта V
Задача 1. Имеются данные о совокупном денежном доходе за месяц и численность семьи (данные условные). Таблица 7.5.1 Данные для построения групповой таблицы
Для выявления зависимости между размером семьи и объемом совокупного денежного дохода произвести группировку семей по их размеру, образовав 2 группы с равными интервалами. По каждой группе семей и в целом по всей совокупности семей рассчитать: 1. Число наблюдений (семей). 2. Численность членов семей всего и в среднем на одну семью. 3. Совокупный денежный доход всего и в среднем на одну семью. Результаты представить в виде итоговой аналитической таблицы. Сделать выводы. Задача 2. Имеются данные о расходовании материала на производство продукции по 3 цехам за два смежных периода. Таблица 7.5.2 Данные для исчисления средних показателей
Вычислить: 1. Средний расход материала на одно изделие: а) за 1 период; б) за 2 период. 2. Абсолютное и относительное отклонение среднего расхода материала во 2 периоде по сравнению с 1 периодом. Задача 3. Группировка магазинов области по размеру товарооборота за I квартал отчетного года имеет следующий вид. Таблица 7.5.3 Данные для исчисления структурных средних величин
Определить: Медиану средней величины магазинов по их товарообороту: а) по формуле; б) графически. Задача 4. В целях изучения норм расхода сырья «А» при изготовлении продукции на предприятиях города было проведено обследование, в результате которого получены следующие данные по распределению израсходованного сырья. Таблица 7.5.4 Данные для исчисления показателей вариации
Вычислить: 1. Средний расход материала «А». 2. Дисперсию. 3. Коэффициент вариации.
Задача 5. По данным задачи 4 с вероятностью 0,997 определить предельную ошибку средней величины и возможные границы, в которых ожидается средний расход сырья для всей партии изготовленных изделий. Принять во внимание, что для получения данных задачи 4 была проведена 15 % механическая выборка.
Задача 6. Общая сумма вкладов населения региона в коммерческие банки в 1 полугодии составила: Таблица 7.5.5 Данные для исчисления показателей динамики
Определить: 1. Базисные и цепные абсолютные приросты, темпы роста и прироста остатков вкладов граждан. Представить полученные данные в таблице. 2. Рассчитать: а) средние остатки вкладов граждан в 1 полугодии; б) среднемесячный абсолютный прирост вкладов; в) среднемесячный темп роста и прироста за весь период. 3. Сформулировать выводы.
Задача 7. Имеются следующие данные по торговой организации. Таблица 7.5.6 Данные для исчисления индексов
Используя систему взаимосвязанных индексов, найти недостающие в таблице показатели.
7.6 Задания для самостоятельной работы для варианта VI Задача 1. Имеются данные об уставном капитале и работающих активах коммерческих банков. Таблица 7.6.1 Данные для построения групповой таблицы, млн. руб.
|
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.68.161 (0.021 с.) |

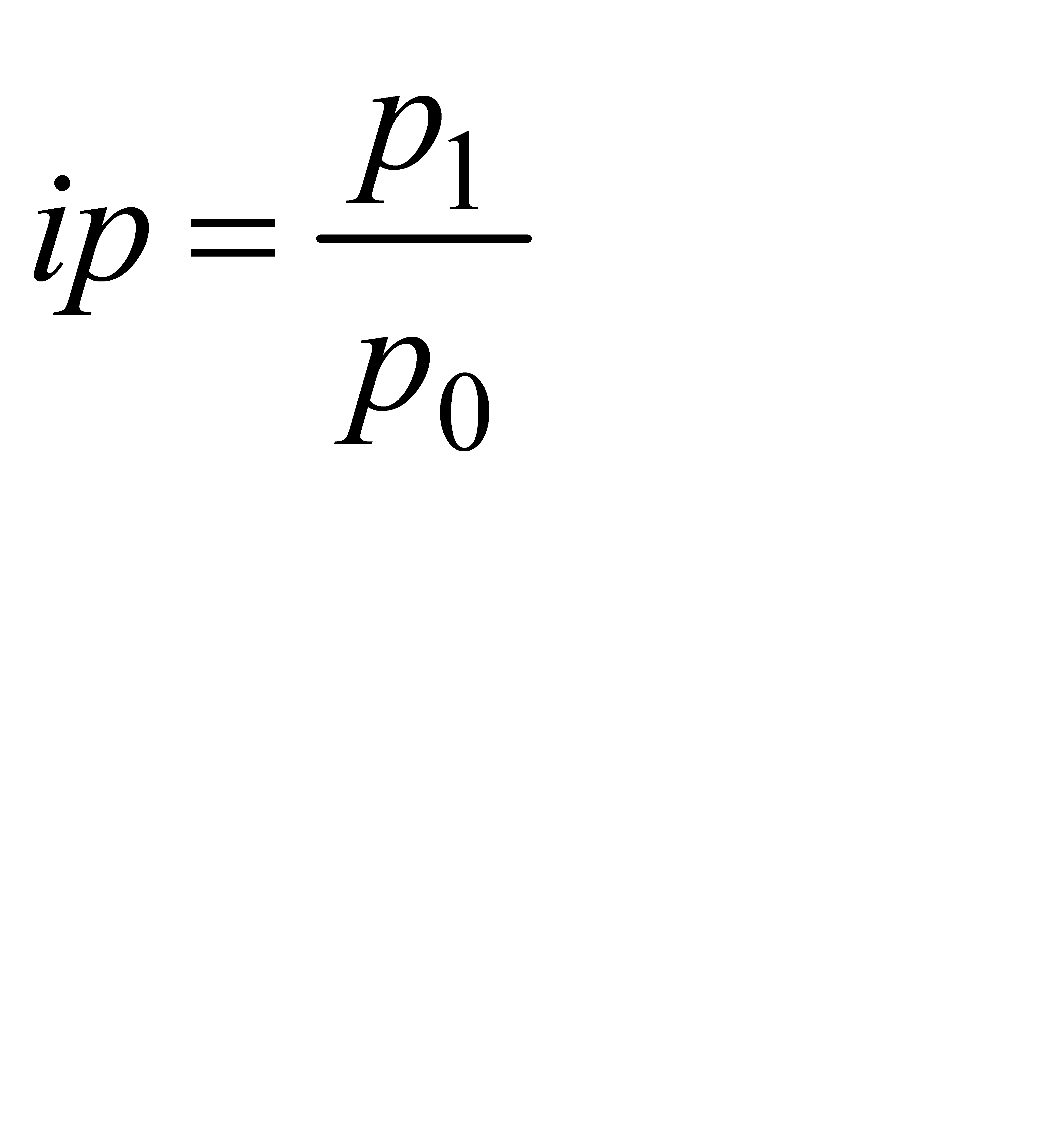 (23)
(23)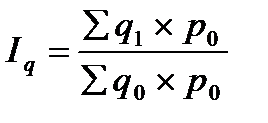 , (24)
, (24) ; (25)
; (25)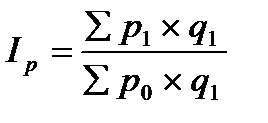 , (26)
, (26)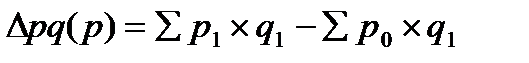 ; (27)
; (27)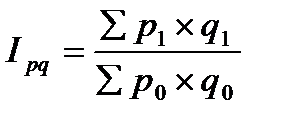 . (28)
. (28)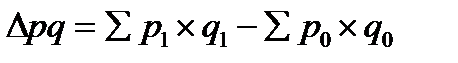 составляет общее абсолютное изменение товарооборота за счёт совместного действия обоих факторов: цен на продукцию и её количества.
составляет общее абсолютное изменение товарооборота за счёт совместного действия обоих факторов: цен на продукцию и её количества.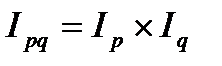 , (29)
, (29)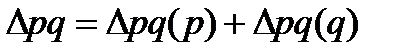 . (30)
. (30)


