
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Статистические показателиСодержание книги
Поиск на нашем сайте
Вопросы 1. Понятие, формы выражения и виды статистических показателей. Функции статистических показателей. 2. Абсолютные и относительные величины, их взаимосвязь и необходимость комплексного применения. 3. Виды средних и способы их расчета. 4. Понятие структурных средних: мода, медиана. 5. Применение графического метода для определения моды и медианы. 6. Использование средних величин в статистическом анализе. [ 1, с. 47–50; 52–70; 2, с. 82–95; 120–137; 3, с. 40–42; 65–72; 5, с. 155–63; 164–176, 6 ] Методические указания к изучению темы Статистический показатель представляет собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности. Абсолютные показатели отражают физические размеры изучаемых процессов и явлений, а так же могут представлять собой объем совокупности, временную характеристику и т.п. Абсолютные показатели выражаются в натуральных, стоимостных или трудовых показателях. Относительный показатель представляет собой результат деления абсолютных показателей. Все используемые на практике относительные величины можно подразделить на следующие виды: относительные величины динамики, плана, реализации плана, структуры, координации, интенсивности и уровня экономического развития, сравнения. Наиболее распространенной формой статистических показателей, используемой в социально-экономических исследованиях, является средняя величина. Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Показатель, представленный в форме средней отражает уровень признака, отнесённый к единице совокупности. Определить среднюю во многих случаях удобнее через исходное соотношение средней (ИСС) или её логическую формулу:
Расчёт большинства конкретных статистических показателей основан на использовании средней арифметической взвешенной:
или средней гармонической взвешенной:
При этом, если известны значения признака (хi) и частоты (fi), следует применить формулу средней арифметической, а если известны варианты и произведение вариант на частоты (w) – формулу средней гармонической величины. Например, рассчитаем среднюю заработную плату по трём предприятиям АО (табл. 2.1), используя различные формулы средних величин.
Таблица 2.1 Данные об оплате труда и численности персонала предприятий АО «Триумф»
Решение. Независимо от имеющихся в нашем распоряжении данных средняя заработная плата может быть получена только через следующее отношение:
Рассмотрим разные варианты расчёта. 1. Предположим, что мы располагаем только данными граф 1 и 2 табл. 2.5. Итоги этих граф содержат все необходимые величины для расчёта искомой средней. Воспользуемся формулой средней: ` 2. Если мы располагаем данными граф 1 и 3, то нам известен знаменатель ИСС, но не известен его числитель. Однако фонд заработной платы можно получить умножением средней заработной платы на численность персонала. В этом случае общая средняя заработная плата рассчитывается по формуле средней арифметической взвешенной:
3. Если в нашем распоряжении имеются только данные о фонде заработной платы и средней заработной платы персонала (графы 2 и 3), т. е. нам известен числитель исходного соотношения, но не известен его знаменатель. Численность работников можно получить делением фонда заработной платы на среднюю заработную плату. Тогда расчёт будет произведён по формуле средней гармонической взвешенной:
Таким образом, полученные тремя способами значения средней заработной платы совпадают. Кроме перечисленных видов средних величин рассчитывают структурные средние: моду и медиану. Мода – значение признака, наиболее часто встречающееся в изучаемой совокупности. Для интервальных вариационных рядов распределения мода рассчитывается по формуле:
где Mo – мода; хМо – нижняя граница модального интервала; hМо – величина модального интервала; fМо – частота модального интервала; fMo-1 – частота интервала, предшествующему модальному; fMo+1 – частота интервала, следующего за модальным. Медианой называется варианта, расположенная в середине упорядоченного вариационного ряда, делящая его на две равные части. Для интервальных вариационных рядов медиана рассчитывается по формуле:
где Ме – медиана; хМе – нижняя граница медианного интервала; hMe – величина медианного интервала; Значение моды и медианы можно определить графически: моду – с помощью построения гистограммы, медиану – при помощи построения кумуляты. Рассмотрим пример определения структурных средних моды и медианы на основании данных о распределении работников предприятия по уровню среднемесячной заработной платы (табл. 2.2). Определить модальный размер заработной платы, рассчитать медиану. Таблица 2.2 Группировка работников предприятия по уровню заработной платы
Решение. Первоначально определим модальный интервал. Наибольшее число работников – 70 человек имеют заработную плату в интервале 700-800 долл., который и является модальным:
Таким образом, наибольшее число работников предприятия получают заработную плату в размере 780 руб. Определим медианный интервал, в котором находится порядковый номер медианы (200: 2 = 100). Для этого подсчитаем сумму накопленных частот. Значение 110 соответствует интервалу 700-800. Это и есть медианный интервал, в котором находится медиана.
Из расчёта следует, что половина работников предприятия имеют заработную плату до 785,7 руб., а другая половина – выше этой величины.
Контрольные вопросы 1. Дайте определение статистическому показателю. 2. Назовите основные функции, которые выполняет статистический показатель. 3. Дайте характеристику видов статистических показателей. 4. Что представляют собой абсолютные величины? 5. В каких единицах измерения их выражают? 6. Назовите примеры абсолютных величин. 7. Что такое относительная величина? 8. В каких единицах измерения выражают относительные величины? 9. Приведите примеры использования относительных величин в анализе экономических и социальных проблем перехода к рыночной экономике.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.55.25 (0.01 с.) |

 . (2)
. (2) (3)
(3) . (4)
. (4) .
.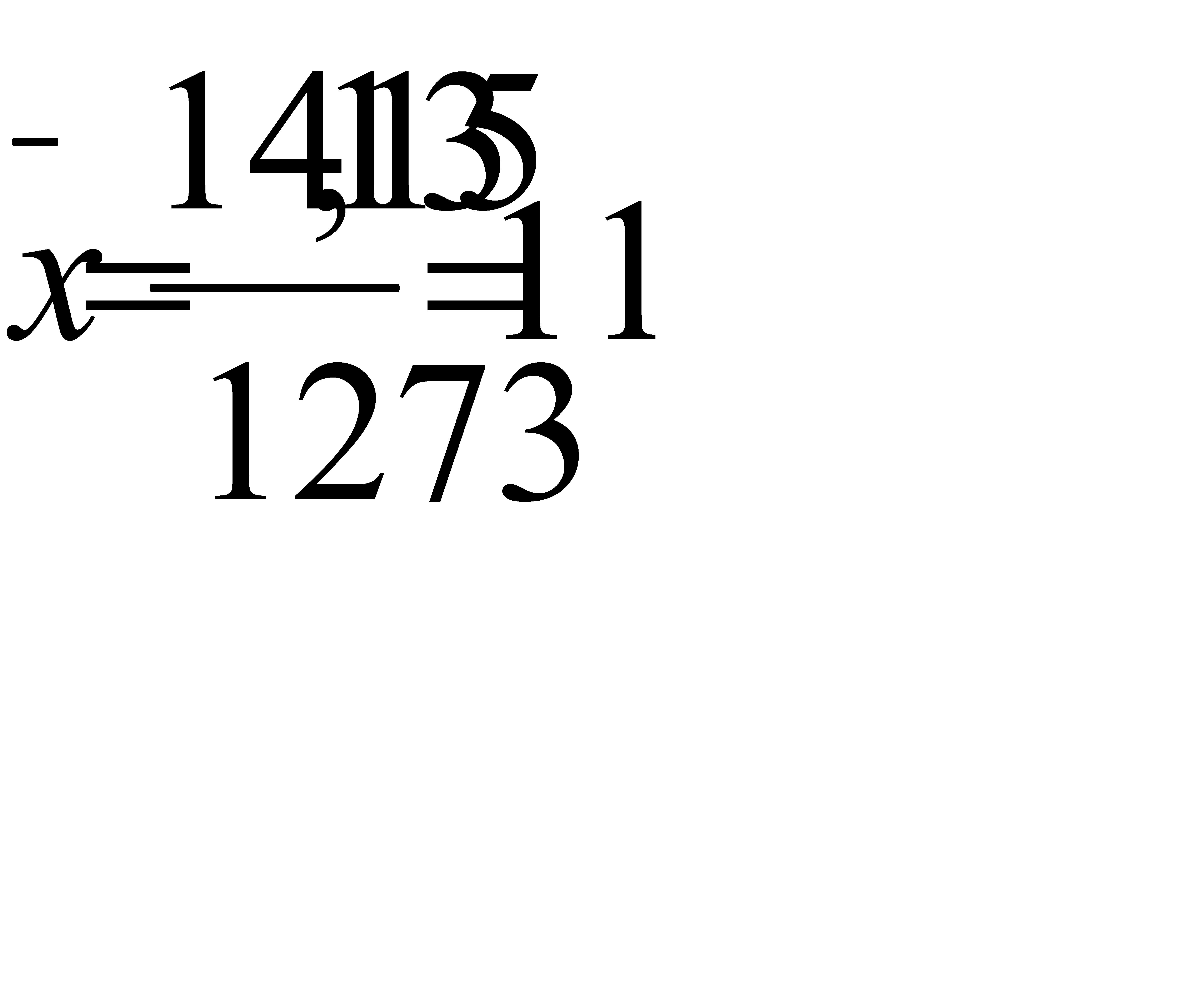 $.
$. $.
$. $.
$.
 , (5)
, (5) , (6)
, (6) – сумма всех частот; SMe-1 – сумма накопленных частот ряда, предшествующих медианному интервалу; fMe – частота медианного интервала.
– сумма всех частот; SMe-1 – сумма накопленных частот ряда, предшествующих медианному интервалу; fMe – частота медианного интервала. $.
$. $.
$.


