
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки для виконання регресійного аналізуСодержание книги
Поиск на нашем сайте
Лабораторний практикум для студентів напрямку підготовки 0501 «Економіка та підприємництво» з дисципліни «Статистика»
Дніпропетровськ
Міністерство освіти і науки України
Лабораторний практикум для студентів напрямку 0501 «Економіка та підприємництво» з дисципліни «Статистика»
Рекомендовано до видання науково-методичної радою академії (протокол № __ від ___________р.)
Дніпропетровськ Лабораторний практикум для студентів напрямку підготовки 0501 з дисциплині “Статистика”/ Укладачі: А. С. Корхін, О. П. Минакова. – Дніпропетровськ: НГУ України, 2002. – 53 с.
Укладачі: А. С. Корхін кандидат технічних наук, доцент кафедри економічної кібернетики та інформаційних технологій О. П. Минакова, асистент кафедри економічної кібернетики та інформаційних технологій.
Відповідальний за випуск завідувач кафедри економічної кібернетики та інформаційних технологій Є. В. Кочура, доктор технічних наук, професор.
Вступ Дисципліна "Статистика" є однією з компонентів циклу загальнопрофесійних дисциплін при підготовці кваліфікованих фахівців для студентів напрямку 0501 «Економіка та підприємництво. Метою дисципліни є формування в студентів базової системи знань в області загальної теорії статистики. Програма орієнтована на вивчення статистики стосовно до аналізу соціально-економічних явищ, і її ролі в плануванні, прогнозуванні й аналізі діяльності промислових підприємств, що функціонують у сучасних макроекономічних умовах. Задачами освоєння матеріалу дисципліни є:
Програма дисципліни включає 13 лабораторних робіт і розрахована на вивчення протягом двох навчальних семестрів. Завдання виконуються на персональному комп’ютері з використанням додатку MS Excel 2000. Завдання треба здавати у письмовому та електронному вигляді. Зміст звіту указан у методичних вказівках до кожної лабораторної роботи. Зміст повинен включати стислу послідовність всіх дій по виконанню лабораторної роботи та відповіді на запитання, які знаходяться наприкінці деяких лабораторних робіт. Вихідні дані для виконання кожної роботи знаходяться у додатку 1 (стор. 31). ЛАБОРАТОРНА РОБОТА STAT-1 Тема: Графічні методи зображення статистичної інформації і їх використання за допомогою персональног комп'ютера. Мета роботи: Вивчення роботи «Мастер диаграмм» у MS Excel 2000 для графічного аналізу статистичних даних. Вихідні дані: таблиця № 1 у додатку 1.
Для найбільш наочного представлення статистичної інформації часто використовують графічні методи відображення. Значення графічного методу в аналізі й узагальненні даних велико. Графічне зображення насамперед дозволяє здійснити контроль вірогідності статистичних показників, тому що, представлені на графіку, вони найбільше яскраво показують наявні неточності, зв'язані або з наявністю помилок спостереження, або із сутністю досліджуваного явища. За допомогою графічного зображення можливе вивчення закономірностей розвитку явища, встановлення істотних взаємозв'язків. Графіки широко використовуються для вивчення структури явищ, їхньої зміни в часі і розміщення в просторі. У них чітко видні основні тенденції розвитку і взаємозв'язку, властивому досліджуваному чи явищу процесу. У MS Excel 2000 мається могутній інструмент для побудови різних графіків. Це убудований у Excel «Майстер діаграм», що дозволяє будувати різні типи діаграм (стандартні і нестандартні), указувати різні параметри діаграм (заголовки, осі, підписи даних і т.д.). У Excel маються наступні типи стандартних діаграм: гистограмма, лінійчата, графік, кругова, кільцева, біржова, крапкова, пузырькова, пелюсткова, поверхня, конічна, циліндрична і пірамідальна. Гистограмма дозволяє представити зміну даних протягом відрізка часу. Діаграми цього типу зручні також для наочного порівняння різних величин. Ось категорій у гистограмме розташовується по горизонталі, ось значень -- по вертикалі. Таке розташування осей підкреслює характер зміни значень у часі. Гистограмма з нагромадженням дозволяє представити відношення окремих складових до їх сукупного значення. На об'ємної гистограммі з перспективою порівнювані значення розташовуються в площині (уздовж двох осей). Лінійчата діаграма дозволяє порівнювати окремі значення. Ось категорій розташована по вертикалі, ось значень -- по горизонталі. Це дозволяє звернути більшу увагу на порівнювані значення, чим на час. Лінійчата діаграма з нагромадженням показує внесок окремих елементів у загальну суму. Кругова діаграма показує відношення розмірів елементів, що утворять ряд даних, до суми елементів. Завжди відображається тільки один ряд даних. Такий тип діаграми доцільно використовувати, коли необхідно підкреслити важливий елемент. Як і кругова діаграма, кільцева діаграма показує відношення частин до цілого, але цей тип діаграми може включати кілька рядів даних. Кожне кільце в кільцевій діаграмі відповідає одному ряду даних. Крапкова діаграма показує відносини між чисельними значеннями в декількох рядах даних, чи відображає двох груп чисел як один ряд координат x і y. Ця діаграма показує нерівні проміжки даних і звичайно використовується для наукових даних. Пузырькова діаграма -- це різновид крапкової діаграми. Розмір маркера даних показує значення третьої перемінної. Пелюсткова діаграма дозволяє порівнювати сукупні значення декількох рядів даних. У пелюстковій діаграмі всі категорії мають власні осі координат, що розходяться променями з початку координат. Лініями з'єднуються значення, що відносяться до одного ряду. Діаграму «Поверхность» доцільно використовувати для пошуку найкращого сполучення в двох наборах даних. Для створення діаграми необхідно виділити осередку, що містять дані, що повинні бути відбиті на діаграмі. Щоб заголовок стовпця чи рядка для нових даних з'явився в діаграмі, в обирані осередки потрібно включити ті, котрі містять цей заголовок. Потім викликаємо “Мастер діаграм”, що знаходиться на панелі інструментів. Для виклику “Мастера діаграм” можна використовувати також пункт меню Вставка/Диаграма... Потім відповідаємо на питання майстра. “Мастер діаграм” складається з 4-х кроків. На 1-му кроці ми вказуємо тип діаграми, у 2-му – указуємо джерело даних, у 3-му – різні параметри діаграми й у 4-му – розташування діаграми. Для редагування вже створених графіків використовується контекстне меню об'єкта, яке викликаємо правої кнопкой миші на виділеному об'єкті (діаграмі). Завдання 1. За допомогою «Мастер диаграмм» побудувати графіки залежності: - розподіл капітальних вкладень по роках; - введення основних фондів по роках. Завдання 2. За допомогою «Мастер диаграмм» побудувати гистограмму для порівняння капітальних вкладень і введення основних фондів по роках. Завдання 3. Виконати угруповання даних по капітальних вкладеннях і введенню основних фондів по десятиліттях і за допомогою «Мастер диаграмм» побудувати дві кругові діаграми. Зміст звіту 1. Назва лабораторної, мета роботи. 2. Послідовність дій при виконанні завдань 1,2,3. 3. Зробити свій висновок. 4. Збудовані графіки здаються викладачу з екрана монітора. ЛАБОРАТОРНА РОБОТА STAT-2 Тема: Статистичний аналіз даних на прикладі аналізу міського населення України. Мета роботи: Вивчення методу угруповання, відносних величин, складання статистичних таблиць і побудова графіків з використанням додатка Excel 2000. Вихідні дані: таблиця № 2.1 (1 варіант), 2.2 (2 варіант), 2.3 (3 варіант) у додатку 1
Завдання 1. Виконати угруповання даних по чисельності міського населення. Порядок виконання робіт 1. Завантажити свою робочу книгу і на вільний лист скопіювати таблицю з вихідними даними по своєму варіанті. 2. Визначити орієнтовно кількість груп по формулі Стерджесса. 3. Визначити границі інтервалів методом послідовного наближення, використовуючи функцію «Частота» (див. Майстер функцій) чи «Гистограмма» (див. меню Сервис, команда Анализ данных) для кожної групи. 4. Остаточно визначити кількість груп і границі групових інтервалів, щоб забезпечити приблизно рівномірний розподіл міст по групах. 5. Заповнити таблицю 1, використовуючи функцію «Частота», див. «Мастер функций». 6. Заповнити таблицю 2, використовуючи функцію «СУММЕСЛИ», див. Мастер функций.
Таблиця 1
Таблиця 2
Завдання 2. Побудова діаграм розподілу загальної кількості населення по групах.
Порядок виконання робіт
1. Побудувати гистограми для кожного року (варіаційні ряди), де Y – кількість міст, X-чисельність населення в місті (по групах). 2. Побудувати кругову діаграму для 1990 року розподілу загальної кількості населення по групах.
Завдання 3. Визначити відносні величини динаміки – базисні і ланцюгові, для кожної групи, окремо по кількості міст і загальній кількості населення.
Порядок виконання робіт
1. Заповнити таблицю 3 2. За даними таблиці побудувати графіки наступних величин: - коефіцієнти росту ланцюгові і базисні на одному графіку; - темпи росту ланцюгові і базисні на одному графіку; - темпи приросту ланцюгові і базисні на одному графіку. 3. По одній із груп зробити 3 графіка: - ланцюгові і базисні коефіцієнти росту в залежності від номера року; - ланцюгові і базисні темпи росту в залежності від номера року; - ланцюгові і базисні темпи приросту в залежності від номера року.
Таблиця 3
Зміст звіту
1. Назва лабораторної, мета роботи. 2. Послідовність дій при виконанні завдань. 3. Зробити свій висновок. 4. Заповнені таблиці здаються викладачу з екрана монітора.
ЛАБОРАТОРНА РОБОТА STAT-3
Тема: Визначення середніх величин і їх дисперсії. Мета роботи: Обчислення середньої арифметичної, середньої гармонійної і дисперсії. Вихідні дані: таблиця № 3, 4 (1-й варіант) і таблиця 5, 6 (2-й варіант) у додатку 1.
Порядок виконання робіт 1. Завантажити свою робочу книгу і на вільний лист скопіювати таблицю з вихідними даними по своєму варіанті. 2. Визначити середню зарплату одному працюючему по об'єднанню за даними таблиці 3, 4 і таблиці 5, 6. 3. Для розрахунку використовувати формулу середньозваженої арифметичної (для таблиці 3, 4) і середньозваженої гармонійний (для таблиці 5, 6).
4. Визначити дисперсію зарплати одному працюючому по об'єднанню, використуючи функцію ДИСП Мастера функцій.
Зміст звіту:
1. Назва лабораторної роботи, мета роботи. 2. Послідовність дій при виконанні пунктів 1-4. 3. Висновок. 4. Заповнені таблиці здаються викладачу з екрана монітора. ЛАБОРАТОРНА РОБОТА STAT-4 Тема: Визначення по малій вибірці теоретичного закону розподілу. Мета роботи: на основі оцінок коефіцієнтів асиметрії й ексцесу визначити, чи підкоряється заданий варіаційний ряд нормальному закону розподілу. Для розрахунків використовувати Excel 2000. Вихідні дані: таблиця № 7 у додатку 1. Порядок виконання робіт 1. Завантажити свою робочу книгу і на вільний лист скопіювати таблицю з вихідними даними по своєму варіанті. 2. Розрахувати оцінки коефіцієнтів асиметрії й ексцесу й інші величини за допомогою функції "Анализ данных". Для цього виконати наступні команди: Сервис/Анализ данных/Описательная статистика. У появившемся меню у вікно "Входной интервал" увести вихідний варіаційний ряд, у вікні "Итоговая статистика" поставити галочку, у вікні "Выходной интервал" вказати адресу крайнього лівого осередку масиву вихідних даних. Масив складається з 2-х стовпців: - 1-й - назва статистичних характеристик - 2-й - числові значення цих характеристик. 3. Обчислити статистику
яка має хі-квадрат розподіл (тут n-обсяг вибірки, Коефіцієнти асиметрії та экцеса характеризують форму розподілу ознаки сукупності. Коефіцієнт асиметрії може бути позитивним і негативним. У першому випадку мова йде про правосторонню асиметрію, а в другому – про лівосторонню. Для симетричних розподілів може бути розрахований коефіцієнт экцеса. Існують два види розподілів: гостровершинне (коефіцієнт экцеса позитивний) і плосковершинне (коефіцієнт экцеса негативний). У нормальному розподілі коефіцієнт экцеса дорівнює нулю. 4. По К знайти імовірність дотримання гіпотези про нормальний розподіл заробітної плати. Для цього використовувати функцію ХИ2РАСП (див. Статистичні функції в "Мастере функций"). Ця функція повертає однобічну імовірність розподілу хі-квадрат, має два аргументи: перший – це значення, для якого потрібно обчислити розподіл (у нашому випадку – значення К), другий – число ступенів волі. У нашому випадку треба задати число ступенів волі – 2. Прийняти рішення, чи підкоряється заданий варіаційний ряд нормальному закону розподілу. Зміст звіту: 1. Назва лабораторної роботи, мета роботи. 2. Послідовність дій при виконанні пунктів 1-4. 3. Висновок. ЛАБОРАТОРНА РОБОТА STAT-5
Тема: Визначення по великій вибірці теоретичного закону розподілу. Ціль роботи: за допомогою критерію Пирсона визначити, чи підкоряється заданий варіаційний ряд нормальному закону розподілу. Вихідні дані: таблиця № 8 у додатку 1 Порядок виконання роботи 1. Завантажити свою робочу книгу і на вільний лист скопіювати вихідний часовий ряд про врожайність зернових у 500 фермерських господарствах і табличній формі, куди будуть заноситися результати розрахунків. 2. Визначити число груп, на які розбивається варіаційний ряд по формулі Стерджесса: nгр=1+3,322lg(n), де n- обсяг вибірки (n=500). Формулу розрахувати в осередку I2. 3. Визначити ширину групового інтервалу
де x max і x min відповідно максимальна і мінімальна врожайність. Округлити h до числа з одним знаком після коми і занести в осередок I3. 4. Розрахувати параметри закону розподілу: - середнє значення врожайності; - стандартне відхилення врожайності, занести ці значення відповідно в осередки I4 і I5. 5. Визначити праві границі групових інтервалів і занести їх у відповідний стовпець таблиці. Рекомендується границю 1-го інтервалу взяти рівної 38,4 ц/га. 6. Визначити число спостережень у кожній групі за допомогою функції “ Частота” (Мастер функций, категорія “Статистические”). У перше вікно цієї функції уводимо вихідний варіаційний ряд, у друге (двоїчний масив) – праві границі групових інтервалів. Результат занести в другий стовпець таблиці. Для цього необхідно перед його розрахунком виділити місце для результату, а для занесення результату натиснути клавіші Ctrl-Shift-Enter. 7. Визначити теоретичну імовірність влучення в кожен груповий інтервал. 7.1. Визначити значення функції нормального розподілу для правої границі інтервалу. Для цього використовувати функцію НОРМРАСП (Мастер функций). Заповнення вікон цієї функції наступне: x – значення правої границі інтервалу; середнє – середнє значення врожайності; стандартне відхилення – значення цієї величини для врожайності; інтегральний – ИСТИНА (означає, що обчислюється функція розподілу). Результат розрахунків занести у відповідний стовпець таблиці. Рекомендується заповнити вікна тільки для розрахунку функції розподілу для правої границі 1-го інтервалу. Для інших інтервалів шукані величини знайти за допомогою копіювання. 7.2. Розрахувати теоретичну імовірність влучення в кожен інтервал, що дорівнює різниці значень функції розподілу для правого кінця розглянутого інтервалу і цієї ж функції для правого кінця попереднього інтервалу. Занести результат в останню графу таблиці. 8. Розрахувати теоретичні частоти влучення в кожен груповий інтервал. Для цього загальне число спостережень n =500 помножити на теоретичну імовірність влучення у відповідний інтервал. Занести результат в останню графу таблиці. 9. Розрахувати критерій хі-квадрат Пирсона
де:
Результат рішення занести в осередок I6. Перевірити гіпотезу про нормальний закон розподілу врожайності зернових. Для цього використовувати функцію ХИ2РАСП, що дозволяє визначити імовірність дотримання гіпотези. При цьому число ступенів волі S=n-1-q, де q – число оцінених параметрів нормального закону розподілу (див.п.5). Гіпотеза про те, що варіаційний ряд підкоряється обраному теоретичному закону розподілу, приймається, якщо P>=0,2.
Зміст звіту:
1. Назва лабораторної роботи, мета роботи. 2. Послідовність дій при виконанні пунктів 1-9. 3. Висновок. 4. Заповнені таблиці здаються викладачу з екрана монітора
Лабораторна робота STAT-6 Тема: Визначення оцінки середнього значення ознаки в генеральній сукупності і точності його оцінювання. Мета роботи: Визначення оцінки середнього значення і його довірчого інтервалу по малій і великій вибірках з генеральних сукупностей, що підкоряються нормальному закону розподілу. Вихідні дані: таблиці № 9, 8 у додатку 1 Ряд у таблиці № 9 містить мало даних і називається малою вибіркою. Як велику вибірку береться врожайність у 500 фермерських господарствах (ц/га), що є вихідною інформацією для виконання лабораторної роботи Stat_5 (таблиця 8 додатка 1).
Порядок виконання роботи
1. Створити свою робочу книгу, що повинна складатися з 2-х аркушів. На перший аркуш у стовпець А уводиться свій варіант із таблиці 9 додатка 1. На другий аркуш у стовпець А копіюються дані про врожайність з лабораторної роботи Stat_5 (таблиця 8 додатка 1).. Надалі всі розрахунки й остаточні результати приводяться на відповідних аркушах створеної робочої книги. 2. Визначити оцінки середнього значення в генеральній сукупності. - без угруповання даних (мала вибірка)
де xi – значення показника в i – ом спостереженні, n – обсяг вибірки. с угрупованням даних (велика вибірка)
де
fi - число спостережень, що потрапили в i-й інтервал; l – число інтервалів
Указівка: для визначення 3. Визначення точності оцінювання середнього значення в генеральній сукупності – обчислення дисперсії його оцінки. 3.1 Обчислення оцінки дисперсії в генеральній сукупності: - без угруповання даних (мала вибірка) – незміщена оцінка
- с угрупованням даних (велика вибірка)
3.2 Обчислення оцінки дисперсії оцінки середнього значення показника:
4. Визначення довірчого інтервалу з довірчими рівнями (імовірностями):
4.1 Теоретичне обґрунтування: даний метод визначення довірчого інтервалу справедливий, якщо розглянутий показник розподілений нормально. Нехай дисперсія показника в генеральній сукупності точно відома. Тоді:
де u – стандартна нормальна величина з математичним чеканням 0 і дисперсією 1;
Тут, Для великих вибірок Тоді, згідно (8)
де Для малих вибірок Величина
де t – розподіл Стьюдента з n -1 ступенями волі. З (7) довірчий інтервал для
де 4.2 Перевірка гіпотези про нормальний розподіл показника. Вона виконується для малої вибірки, тому що для великої вибірки вона перевірена в лабораторній роботі Stat_5. Перевірка для малої вибірки виконується на основі обчислення статистики До по оцінках коефіцієнтів асиметрії й ексцесу як у лабораторній роботі Stat_4. 4.3 Обчислити довірчі інтервали для великої і малої вибірок і результати занести в таблиці 4 і 5 відповідно кожній вибірці.
Таблиця 4
Таблиця 5
Для обчислення величини u p і tp у (11) і (13) використовувати відповідно функції НОРМСТОБР і СТЬЮДРАСПОБР у Мастере функций. При використанні НОРМСТОБР вводиться у вікно «Вероятность» величина P і результат береться зі зворотним знаком, тому що НОРМСТОБР визначає для заданого значення функції розподілу її аргумент. При використанні СТЬЮДРАСПОБР у вікно «Вероятность» уводиться величина 2p, у вікно «Степени свободы» - число ступенів волі, рівні n-1. Такі обчислення робляться тому, що СТЬЮДРАСПОБР дає значення tp для імовірності 2p.
Контрольні питання:
1. Як збільшується ширина довірчого інтервалу зі збільшенням 2. Як залежить ширина довірчого інтервалу для більшої вибірки від формули його розрахунку ((11) чи (13)) і чому. 3. Яка величина оцінки середнього значення врожайності і її дисперсій є більш точної: по згрупованим чи по не згрупованим даним. 4. Чи можна визначати довірчий інтервал для середнього значення генеральної сукупності, якщо показник не розподілений нормально.
Зміст звіту:
1. Назва лабораторної роботи, мета роботи. 2. Послідовність дій при виконанні пунктів 1-4. 3. Висновок. 4. Заповнені таблиці здаються викладачу з екрана монітора. 5. Відповіді на контрольні запитання. Лабораторна робота STAT-7 Тема: Розробка плану статистичного контролю якості. Мета роботи: Розрахувати плани контролю межі міцності партій газоводопроводних труб. Визначити придатність однієї партії труб на основі вибіркового контролю межі міцності партії труб (контроль по кількісній ознаці). Відповідно до технічних норм межа міцності труб повинний бути не менше величини G=30 кгс/мм2. Вихідні дані: таблиця № 10 у додатку 1.
Порядок виконання роботи
1. Створити у своєму каталозі файл за допомогою табличного процесора Excel і скопіювати в нього дані про межу міцності всіх труб партії (50 штук) (файл Stat_7, таблиця № 10 у додатку 1). 2. Вихідні дані для розрахунку: Розподіл межі міцності – нормальне. Ризик виготовлювача a=0,1; ризик споживача b=0,1, приймальний рівень якості q1=0,005, бракувальний рівень якості q2=0,05. Ризик виготовлювача a - імовірність забракования партії з задовільним (приймальним) рівнем якості q1. Ризик споживача b - імовірність прийняття партії з незадовільним (бракувальним) рівнем якості q2. 3. Обчислити квантили нормального розподілу u(1-q1), u(1-q2), u(1-a), u(1-b) для цього використовувати функцію НОРМОСТОБР у Мастере функций. У ній як аргумент «Вероятность» брати величини (1-q1), (1-q2), u(1-a), u(1-b). 4. Визначити коефіцієнт k, необхідний для розрахунку приймального числа,
5. Визначити число труб, що відбираються від партії для визначення механічних властивостей.
n необхідно округлити до найближчого більшого цілого числа. 6. З наявних у партії труб відібрати випадковим образом n труб (узяти n вимірів). Для цього необхідно за допомогою функції «Генерация случайных чисел» у «Анализ данных» у Excel, одержати n чисел, що відповідають номерам труб, що будуть контролюватися. Для чого потрібно виконати наступні дії. Створити 2 стовпці: 1- й стовпець містить номера труб, 2-й стовпець повинний містити імовірності витягу труби з партії. Вони однакові і рівні 1/число труб у партії. У вікні функції «Генерация случайных чисел» заповнити наступні поля: - число перемінних – 1; - число випадкових чисел – n; - розподіл дискретне; - вхідний інтервал –2 створених стовпці з номерами труб і імовірностями їхнього витягу. - вихідний інтервал - виділяється стовпець з n осередками. У результаті рішення в цьому стовпці буде знаходитися n номерів труб, які необхідно випробувати. З таблиці вихідних даних варто відібрати n значень межі міцності, що відповідають n номерам, отриманим за допомогою функції «Генерации случайных чисел», і занести їх в окремий стовпець, створивши тим самим вибірку даних про контрольовані труби. 7. Знайти середнє значення межі міцності для отриманої вибірки:
де xi – значення межі міцності i-ї труби, n -кількість відібраних труб. Оцінити середнє квадратичне відхилення межі міцності у вибірці:
Середнє значення і середнє квадратичне відхилення межі міцності у вибірці, можна розрахувати за допомогою надбудови «Анализ данных» (функція «Описательная статистика»). 8. Партія труб приймається, якщо де k розраховується по формулі (14), G =30 кгс/мм2 – норма на межу міцності.
Зміст звіту:
1. Назва лабораторної роботи, мета роботи. 2. Послідовність дій при виконанні пунктів 1-8. 3. Висновок. 4. Заповнені таблиці здаються викладачу з екрана монітора
Лабораторна робота STAT-8 Тема:Побудова регресійних моделей. Мета роботи: одержати практичні навички у виконанні кореляційного аналізу, а також у створенні й аналізі однофакторних і багатофакторних регресійних моделей. Вихідні дані: таблиця № 11 у додатку 1 Порядок виконання роботи 1. Виконати кореляційний аналіз для оцінки ступеня зв'язку показників: часу кредитного обороту, середній розмір кредиту, доходу. 2. Для обчислення коефіцієнта кореляції між наборами даних необхідно в меню Сервис вибрати команду «Анализ данных», а в списку, що з'явився, вибрати рядок «Корреляция». 3. Створити однофакторну регресійну модель залежності доходу від тривалості кредитного обороту, лінійну по регрессору і параметрах. а) Побудувати рівняння регресії. Визначити коефіцієнт детермінації, F – відношення, середнє квадратическое відхилення залишків, оцінити адекватність моделі. б) Побудувати довірчі інтервали для коефіцієнтів регресії з імовірністю 0,95. 4. Створити багатофакторну регресійну модель, що характеризує залежність доходу від часу кредитного обороту і середнього розміру кредиту: а) Побудувати лінійну по параметрах і регрессорам модель. Визначити коефіцієнт детермінації, F –
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.244.34 (0.016 с.) |


 середньозважена арифметична (1)
середньозважена арифметична (1)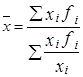 середньозважена гармонійна (2)
середньозважена гармонійна (2) , (3)
, (3) -оцінка коефіцієнта асиметрії,
-оцінка коефіцієнта асиметрії,  оцінка -коефіцієнта ексцесу).
оцінка -коефіцієнта ексцесу). , (4)
, (4)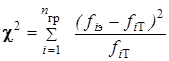 , (5)
, (5) - фактична частота влучення в інтервал i;
- фактична частота влучення в інтервал i; - теоретична частота влучення в інтервал i.
- теоретична частота влучення в інтервал i. , (6)
, (6) , (7)
, (7) - значення середини i-го інтервалу групування;
- значення середини i-го інтервалу групування; по формулі (5) використовувати результати групування врожайності в лабораторній роботі Stat_5. При цьому в якості
по формулі (5) використовувати результати групування врожайності в лабораторній роботі Stat_5. При цьому в якості  взяти середину першого інтервалу, нижня межа якого xmin, а верхня 38,4 ц/га.
взяти середину першого інтервалу, нижня межа якого xmin, а верхня 38,4 ц/га. , (8)
, (8)

 , (9)
, (9) =0,683; 0,954; 0,997; 0,999
=0,683; 0,954; 0,997; 0,999 , (10)
, (10) – середнє значення показника в генеральній сукупності;
– середнє значення показника в генеральній сукупності; - значення дисперсії оцінки середнього:
- значення дисперсії оцінки середнього:  .
. - дисперсія показника в генеральній сукупності.
- дисперсія показника в генеральній сукупності. .
. , відкіля довірчий інтервал для
, відкіля довірчий інтервал для  :
: ,
,  , (11)
, (11)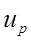 - 100% - ная крапка стандартного нормального розподілу.
- 100% - ная крапка стандартного нормального розподілу. ,
, , (12)
, (12) :
:
 (13)
(13) - 100% -ная крапка розподілу Стьюдента.
- 100% -ная крапка розподілу Стьюдента. /
/  Розподілений нормально (см. формулу 11)
Розподілений нормально (см. формулу 11)
 Розподілений нормально (см. формулу 13)
Розподілений нормально (см. формулу 13)
 .
. , (14)
, (14) , (15)
, (15) , (16)
, (16) . (17)
. (17) , і бракується, якщо
, і бракується, якщо  . Приймальне число:
. Приймальне число:  ,
,


