
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ББ Style Сортировка любых типов данныхСодержание книги
Поиск на нашем сайте
1. Простые обменные сортировки: Обменом, Вставками, Выбором 2. Сортировка в разных направлениях (Шейкер) 3. Быстрая сортировка (Хоора) 4. Сортировка слиянием 5. Сортировка с убывающим приращением (Шелла) 6. Сортировка с помощью дерева
Объект называется рекурсивным, если он содержит сам себя или определен с помощью самого себя. Рекурсия – обращение процедуры или функции самой к себе, прямо или косвенно. Когда функция обращается сама к себе, каждое последующее обращение сопровождается получением ею нового набора автоматических переменных, независимых от предыдущего набора. Программы, написанные с помощью рекурсии, не обеспечивают ни экономии памяти, ни быстродействия; по сравнению с нерекурсивными программами они часто короче, а также намного легче для написания и понимания. Рекурсивные программы особенно удобны для обработки рекурсивно определяемых структур данных вроде деревьев. Пример использования рекурсии– переворачивание строк, быстрая сортировка, предложенная Хоаром, подсчет частоты встречаемости для любых слов, реализуемой с использованием бинарных деревьев.
Рекурсии в математике: 1. а)0! б) n!=n*(n-1)! – эта формула позволяет вычисление любого нового значения на основе предыдущего его значения. 2. а) 1 – натуральное число б) целое число, следующее за натуральным, есть натуральное число
Рекурсия выполняет медленнее, чем обычный цикл. т.к при каждом входе в подпрограмму её локальные переменные размещаются в программном стеке. Тем не менее, алгоритмы, реализуемые с помощью рекурсии, получаются значительно короче. Древовидные структуры. Дерево – это структура, содержащая узел T, с которым связано конечное число древовидных структур с базовым типом T, называемых поддеревьями. Узел, который не имеет потомков, называется терминальным или листом. Узел, не являющийся терминальным, называется внутренним узлом. Линии связей между узлами называются ветвями дерева. Число ветвей, которые надо пройти, чтобы продвинуться от корня A к узлу B, называется длиной пути. Каждый из узлов в таком представлении дерева находится на определенном уровне. Корень дерева имеет уровень, равный 1. Максимальный уровень какого-либо узла называется его глубиной или высотой. Деревья, имеющие степень ветвления больше двух, называются сильно ветвящимися деревьями. Далее рассматриваются бинарные деревья. Бинарное дерево– дерево, каждый узел которого соединен не более чем с 2мя поддеревьями.Информационное поле узла дерева может быть любого типа, определенного ранее, а связи между узлами – это ссылки на узлы того же типа. Type node=^nnode; nnode = record date: <тип данных>; left, right: node; end; var root, p, q: node; Если узел является терминальным, тогда поле ссылки равно null. Основные операции над деревом: 1.Создание дерева 2.Поиск элемента - перемещение по дереву 3.Удаление элемента. 4.Вставка элемента. 5.Упорядочить деревья по заданному признаку (не только сортировка). Cбалансированное дерево. Сбалансированным считается дерево, если на каждом его уровне располагается максимально возможное число узлов поровну слева и справа. Для построения идеально сбалансированного дерева минимальной высоты нужно располагать максимально возможное число узлов на всех уровнях, кроме самого нижнего. Алгоритмически это реализуется распределением узлов поровну справа или слева от каждого узла:
1. Выбрать один узел в качестве корня 2. Построить левое поддерево ® nl=n div 2 3. Построить правое поддерево ® nr=n-nl-1 Root:=nil; New(p); with p^ do begin date:=x; left:=nil; rigth:=nil; end; Root:=p;
Обход дерева - это некоторая последовательность посещения всех его вершин. Инфиксная форма. Это обычный вариант прочтения арифметических выражений, когда знак операции помещается между операндами. Порядок вычисления выражения слева направо в соответствии с приоритетом операций. Скобки изменяют порядок вычислений. SIN (X) *C – D+E/F/(G+H) Префиксная форма. Вариант прочтения арифметических выражений, когда знак операции помещается перед операндами. + - * SIN(X)CD/EF/+GH Постфиксная форма (Обратная польская запись). Вариант прочтения арифметических выражений, когда знак операции помещается после операндов. SIN(X) C*D-EFGH+//+ Обратный обход/постфиксный обход: Начинаем обход дерева с самого левого листа. Поднимаемся к знаку. Далее спускаемся к листу. Прочитанное выражение будет обычной формой записи выражений.
Begin if p<> nil then Begin Infixprint(p^.left); write(p^.date); Infixprint(p^.right); end; end; Постфиксный обход: читаем дерево снизу вверх, как показано на рис.
Begin if p<> nil then Begin Postprint(p^.left); Postprint(p^.right); write(p^.date); end; end; Прямой обход/Префиксный обход: результатом прямого обхода дерева будет префиксный вариант записи этого выражения. 1. Начать с корня дерева. 2. Пометить текущую вершину. 3. Совершить прямой обход левого поддерева. 4. Совершить прямой обход правого поддерева.
Begin if p<> nil then Begin write(p^.date); Prefprint(p^.left); Prefprint(p^.right); end; end; Структуры данных типа дерева. Основные операции над бинарными деревьями. Решение задачи сортировки с помощью дерева. Примеры программирования операций над деревьями. Древовидные структуры. Дерево – это структура, содержащая узел T, с которым связано конечное число древовидных структур с базовым типом T, называемых поддеревьями. Верхний узел дерева – это корень. Каждый новый узел – это новый уровень дерева и, соответственно, потомок предыдущего узла. Если узел не имеет потомков – он называется листом (терминальный узел). Элемент, не являющийся терминальным – внутренний узел. Путь к следующему уровню – ребро дерева (ветвь). Число “ветвей” определяет длину пути к определенному узлу. Бинарное дерево – дерево, каждый узел которого соединен не более чем с 2мя поддеревьями. Для построения идеально сбалансированного дерева минимальной высоты нужно располагать максимально возможное число узлов на всех уровнях, кроме самого нижнего. Алгоритмически это реализуется распределением узлов поровну справа или слева от каждого узла.
Рекурсивная процедура, реализующая такую последовательность построения, должна состоять из следующих действий:
1. Выбрать один узел в качестве корня 2. Построить левое поддерево ® nl=n div 2 3. Построить правое поддерево ® nr=n-nl-1 Root:=nil; New(p); with p^ do begin date:=x; left:=nil; rigth:=nil; end; Root:=p;
Если узел является терминальным, тогда поле ссылки равно null. Основные операции над деревом: 1.Поиск элемента. 2.Удаление элемента. 3.Вставка элемента. 4.Упорядочить деревья по заданному признаку (не только сортировка). 5. Перемещение по дереву Cбалансированное дерево. Сбалансированным считается дерево, если на каждом его уровне располагается максимально возможное число узлов.
Function Poisk(var t:node;r:integer):boolean; var p:node; flag:boolean; Begin flag:=false; p:=t; while (p<> nil) and not flag do if r = p^.date then flag:=true ® найден искомый элемент else if r > p^.date then p: = p^.left else p: = p^.right; ® движение по узлам дерева Poisk: =flag;
2. Удаление элементов созданного дерева. 2.1. Удаление листа – удаляется ссылка на лист из соответствующего поддерева 2.2. Удаление узла с одной ссылкой – ссылку верхнего узла надо заменить на удаляемую ссылку 2.3. Удаляемый узел содержит две ссылки – удаляемый узел замещается самым правым узлом левого поддерева или самым левым узлом правого поддерева
If r^. right =nil then begin q^. date:=r^. date; - запоминаем значение qk:=r; - сохраняем найденный узел r:=r^. Left; Dispose(qk); end else {движение по правому поддереву}
Бинарное дерево поиска можно использовать для сортировки. Для этого берётся пустое дерево, к нему добавляют все элементы массива, а затем, используя алгоритм «Обход дерева», записывают элементы дерева в массив в возрастающем порядке. pTree = ^ Tree;Tree = classpublic left,right: pTree; // левое и правое поддеревья key: integer; // ключ constructor Create (k: integer);…. end; // insert (добавление нового поддерева (ключа)). сравнить ключдобавляемого поддерева (К) с ключом корневого узла (X).Если K>=X, рекурсивно добавить новое дерево в правое поддерево.Если K<X, рекурсивно добавить новое дерево в левое поддерево.Если поддерева нет, то вставить на это место новое дерево procedure Tree.insert(aTree: pTree); begin if (aTree^.key < key) then begin if (left <> nil) then begin left^.insert(aTree); else left:= aTree; end; else if (right <> nil) then begin right^.insert(aTree); else right:= aTree; end; end; end;/* traverse (обход)Рекурсивно обойти левое поддерево. Применить функцию Write(печать) к корневому узлу. Рекурсивно обойти правое поддерево. */ procedure Tree.traverse; begin if (left <> null) then begin left^. traverse; end; write (key); if (right <> null) then begin right ^. traverse; end; end;
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.233.156 (0.007 с.) |

 3. Кривая Гильберта
3. Кривая Гильберта Поворотом можно получить кривые Гильберта любого порядка. Кривая следующего порядка получается соединением четырех кривых вдвое меньшего размера.Так строятся лабиринты. Кривые 1 и 2 порядков
Поворотом можно получить кривые Гильберта любого порядка. Кривая следующего порядка получается соединением четырех кривых вдвое меньшего размера.Так строятся лабиринты. Кривые 1 и 2 порядков Procedure Infixprint(var p:nn);
Procedure Infixprint(var p:nn); Procedure Postprint(var p:nn);
Procedure Postprint(var p:nn); Procedure Prefprint (var p:nn);
Procedure Prefprint (var p:nn);
 n=1 n=2 n=3 n=4 n=5
n=1 n=2 n=3 n=4 n=5


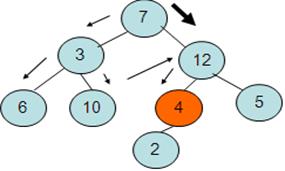 1. Поиск – это движение по дереву
1. Поиск – это движение по дереву end;
end;


