
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Массивы. Исследование и поискСодержание книги
Поиск на нашем сайте
1. Выбрать из массива A(N) (N задано) все элементы, делящиеся на 7. 2. Выбрать из массива A(N) (N задано) все элементы, делящиеся на 5, но не делящиеся на 3 и 7. 3. Дан массив целых чисел A(n)(n), и натуральное k (0<=k<n). Напишите программу, которая прибавляла бы к каждому элементу k-ой строки элемент, принадлежащий этой строке и главной диагонали. 4. Вычислить количество положительных, отрицательных и нулевых элементов в массиве A(n). 5. Заменить максимальный элемент массива А(k) его индексом. 6. Замените минимальный элемент массива А(k) его удвоенным индексом. 7. Заменить все положительные элементы массива A(n) нулями. 8. Вычислить произведение сумм положительных и отрицательных элементов массива A(n). 9. Найти минимальный элемент массива B(n). 10. Найти максимальный элемент массива M(n)(k). 11. Найти максимальный элемент среди отрицательных элементов массива A(N). 12. Найти минимальный элемент среди положительных элементов массива B(K). 13. Определить количество элементов, равных максимальному элементу массива C(N). 14. Требуется ввести последовательность чисел a1,a2,...,an и проверить, есть ли среди них отрицательные. Если они есть, вывести новую последовательность, состоящую из отрицательных членов исходной последовательности, записанных в том же порядке, в каком они встречались в исходной. 15. В одномерном массиве требуется найти наименьший элемент и номер первого такого элемента, если их несколько. 16. Дан массив целых чисел A(n)(k). Создайте программу, находящую наибольший и наименьший элементы этого массива и индексы всех вхождений этих элементов. 17. Напишите программу, находящую в двухмерном массиве номера строк с наибольшей суммой элементов. 18. Для целочисленного массива А(n), определить, является ли сумма его элементов четным числом. 19. В данной последовательности целых чисел найти количество различных нечетных отрицательных чисел. 20. Написать программу определения количества элементов, удовлетворяющих условию 0<А(i)≤i в целочисленном массиве А(n). 21. Найти все локальные минимумы массива А(n). Локальные минимумы одномерного массива - это элементы, которые меньше двух рядом стоящих с ним элементов. Например, массив с элементами 7,4,8,3,6,5,3,2 имеет два локальных минимума - 4 и 3. 22. Определить, имеются ли в целочисленном массиве С(n), два подряд идущих нулевых элемента.
23. В массиве А(n) подсчитать количество четверок А(i), A(i+1),A(i+2), A(i+3), в каждой из которых все элементы различны. 24. Найти наибольшее из всевозможных попарных произведений элементов массива А(n). 25. Назовем максимальный элемент матрицы S(N)(M) главным Написать программу, которая находит произведение чисел той строки матрицы, в которой расположен главный элемент. 26. Дан целочисленный массив А(М). Сосчитать, сколько различных чисел в этом массиве. 27. Дан двухмерный целочисленный массив А(n)(k). Известно, что среди его элементов два и только два равны между собой. Напечатать их индексы. 28. Заданы натуральное число N и целочисленный массив A(N). Найти длину самой длинной последовательности нулей в массиве. 29. Для заданной матрицы размером NxN найти такие k, что k-я строка матрицы совпадает с k-м столбцом. 30. Говорят, что матрица имеет Седловую точку a(i)(j), если a(i)(j) является минимальным в i-той строке и максимальным в j-том столбце. Найти пары (номер строки, номер столбца) для всех Седловых точек заданной матрицы. 31. Для заданной целочисленной матрицы (двухмерного массива) найти минимум среди сумм модулей элементов диагоналей, параллельных главной диагонали матрицы. 32. Задан одномерный массив A(N), состоящий только из нулей и единиц. Проверьте, строго ли они чередуются. 33. Задана последовательность из N чисел. Составить программу нахождения самой длинной возрастающей подпоследовательности данной последовательности. 34. Задана последовательность из N чисел. Найти самую длинную подпоследовательность, обладающую следующим свойством: A(i)<A(i+1)>A(i+2)<A(i+3)>A(i+4)<... 35. Для данной матрицы B(n)(n), содержащей целые числа, найти
36. Числовая прямая разбита на произвольные отрезки точками a1, a2, a3 … an Выясните, какому из отрезков принадлежит данная точка X. 37. Определить, сколько чисел входят в данный одномерный массив только по одному разу. 38. Определить, сколько чисел входят в данный одномерный массив более, чем по одному разу. 39. Модой массива элементов называется число M, которое встречается в массиве наиболее часто. Если в массиве имеется несколько наиболее часто встречающихся элементов и число их вхождений совпадает, то считается, что массив не имеет моды. Напишите программу, которая либо вычисляет моду массива, либо устанавливает, что последний ее не имеет.
40. Даны две совокупности чисел a1…an, b1…bn. Вычислить значения величины
41. Даны последовательности целых a1…an, b1…bn и натуральные m и n. Распечатать значения функции 42. В векторе действительных чисел А(n+1) заданы коэффициенты многочлена Anxn+ An-1xn-1+ …+A1x1+ A0Вычислить значения многочлена и его производной в точке х и распечатать. 43. Даны два целочисленных вектора А(n) и В(k). Распечатать все элементы, которые входят в оба вектора. 44. Дан вещественный вектор A(n). Получить сумму его элементов, принадлежащих отрезку (x, y) и напечатать. 45. Даны два вектора х(n) и у(n) координат точек на плоскости. Найти среди них точку, наиболее близко расположенную к началу координат. 46. Найти произведение ненулевых элементов в одномерном числовом массиве и напечатать. 47. Дана матрица действительных чисел В(n)(k). Найти сумму минимальных элементов её строк и распечатать. 48. Вводится целочисленная квадратная матрица С(n)(n). Определить номера строк, которые образуют палиндромы (симметричные последовательности, например как строки 1 и 3 в следующей матрице) 1 5 3 -2 1 2 1 4 5 6 ─┐ 3 5 7 13 -9 ├─ 6 5 4 1 2 ─┘ 1 7 9 10 13 Модификация массивов 1. В одномерном массиве переставьте первый и последний элементы местами. 2. Переставьте элементы одномерного массива в обратном порядке. Нового массива не заводить. 3. Осуществите циклическую перестановку элементов одномерного массива: первый элемент должен стать вторым, второй - третьим и т.д., последний - первым. Нового массива не заводить. 4. Из массива В(k) убрать все отрицательные элементы, заменив их на значения предыдущих элементов. 5. Дан одномерный массив N(5). Все его элементы, не равные 0 переписать, сохраняя их порядок в начало массива, а нулевые - в конец массива (новый массив не заводить!). 6. Элементы главной диагонали В(i)(i) квадратной матрицы B(n)(n) поставить на место максимального элемента в этой строке. 1Главная диагональ образована из элементов матрицы, имеющих одинаковые индексы строки и столбца. Главную диагональ имеют только квадратные матрицы! 7. В массиве X(M) каждый элемент равен 0, 1 или 2. Переставить элементы массива так, чтобы сначала располагались все 0, затем 1, и, наконец, все 2. (Дополнительного массива не заводить.) Указание. При решении этой задачи, ничего не нужно переставлять. Нужно сосчитать, сколько в массиве нулей, единиц и двоек, и заполнить массив требуемым образом. 8. Характеристикой столбца целочисленной матрицы назовем сумму модулей его отрицательных нечетных элементов. Переставляя столбцы заданной матрицы, расположить их в соответствии с ростом характеристик. 9. "Сожмите" массив, "выбросив" каждый второй его элемент (дополнительные массивы использовать не разрешается!). 10. Целое неотрицательное число М задано массивом своих двоичных цифр a(1), a(2),..., a(n-1), т.е.М=a(n-1)·2n-1+a(n-2) 2n-2+...+a(1) 2+a(0), где a(i)=0 или a(i)=1 (i=0,1,2,...,n-1). Напечатать массив двоичных цифр числа М+1. 11. Транспонируйте матрицу (двухмерный массив), содержащую одинаковое количество строк и столбцов. 12. В заданном одномерном массиве поменяйте местами элементы в парах "элемент с нечетным номером - элемент с четным номером" (дополнительные массивы не использовать).
13. Объединить элементы массивов В и С, содержащих по Т элементов, в массив А таким образом, чтобы в массиве А на четных местах были элементы массива В, а на нечетных местах - элементы массива C (A, B, C - одномерные массивы). 14. Дан вещественный вектор А(n), такой что a1≤a2≤...≤an и число В. Построить вектор С(n+1), элементами которого являются элементы вектора А и число В, упорядоченный по невозрастанию. ЛАБОРАТОРНАЯ РАБОТА 7. 7.1 ЦЕЛЬ РАБОТЫ Познакомиться с простейшими классическими алгоритмами сортировки в регулярном типе данных, а также с основными алгоритмами поиска в массивах. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Под сортировкой обычно понимают процесс перестановки элементов данного множества в определенном порядке. Цель сортировки - облегчение последующего поиска элементов в отсортированном множестве. В этом смысле элементы сортировки присутствуют почти во всех задачах, относящихся к информатике. Ниже мы рассмотрим методы сортировки элементов в массивах (методы сортировки массивов). Основное требование к методам сортировки массивов - экономное использование памяти. Это означает, что переупорядочивание элементов нужно выполнять на одном и том же месте и что методы, которые пересылают элементы из массива А в массив В, не представляют для нас интереса. Проблема сортировки массивов относится в информатике к классическим. Она кажется простой, ведь всем приходилось выполнять какую-либо механическую сортировку, была ли то раскладка игральных карт, гардеробных номерков, карточек из библиотечного каталога или денежных счетов. Однако простота эта иллюзорна. Хотя первые программы сортировки были написаны Дж. фон Нейманом в 1945 г., какого-либо значительного продвижения в теории сортировки не наблюдалось в течение последующих двадцати лет. Рассмотрим несколько методов сортировки массивов. Для определенности, приведем методы сортировки (упорядочивания) векторов по неубыванию. Пусть n - число элементов вектора A, а iизменяется от 0 до n-2. 1. Вектор называется упорядоченным по неубыванию, если для всех i выполнено A(i)<=A(i+1). 2. Вектор называется упорядоченным по невозрастанию, если для всех i выполнено A(i)>=A(i+1). 3. Вектор называется упорядоченным по убыванию, если для всех i выполнено A(i)>A(i+1). 4. Вектор называется упорядоченным по возрастанию, если для всех i выполнено A(i)<A(i+1). Сортировка обменом
Сортировка обменом - метод, при котором все соседние элементы массива попарно сравниваются друг с другом и меняются местами в том случае, если предшествующий элемент больше последующего. В результате этого, максимальный элемент постепенно смещается вправо и, в конце концов, занимает крайнее правое место в массиве, после чего он исключается из дальнейшей обработки. Затем процесс повторяется, и свое место занимает второй по величине элемент, который также исключается из дальнейшего рассмотрения. Так продолжается до тех пор, пока вся последовательность не будет упорядочена. Сортировку обменом называют еще «пузырьковой» (сравнение с всплытием пузырьков воздуха в жидкости). Совершенно ясно, что если на очередном проходе массива не будет сделано ни одного обмена, то массив уже упорядочен. Если мы будем фиксировать этот факт, то несущественное усложнение процедуры сортировки может дать существенный выигрыш в скорости. (См. Пример 1.) Сортировка выбором При этом методе сортировки в неупорядоченной последовательности выбирается минимальный элемент, который исключается из дальнейшей обработки, а оставшаяся последовательность элементов принимается за исходную. Процесс повторяется до тех пор, пока все элементы не будут выбраны. Очевидно, что все выбранные элементы образуют упорядоченную последовательность. Выбранный в исходной последовательности минимальный элемент размещается на предназначенном ему месте упорядоченной последовательности несколькими способами: а) минимальный элемент после i-го просмотра перемещается на i-е место (i=1,2,3,...) другого специально созданного массива, а в старом, исходном, на месте выбранного размещается какое-то очень большое число, превосходящее по величине любой элемент сортируемого массива. Измененный таким образом массив принимается за исходный, и осуществляется следующий просмотр; (См. Пример 2.) б) минимальный элемент после i-го просмотра перемещается на i-е место (i=1,2,3,...) заданного массива, а элемент с i-го места - на место выбранного. После каждого просмотра упорядоченные элементы (от первого до элемента с индексом i) исключаются из дальнейшей обработки, т.е. размер каждого последующего обрабатываемого массива на единицу меньше размера предыдущего. Сортировка включениями При сортировке включениями из неупорядоченной последовательности элементов поочередно выбирается каждый элемент, сравнивается с предыдущим (уже упорядоченным) списком и помещается на соответствующее место в последнем. (См. Пример 3.)
|
||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 822; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.35.211 (0.011 с.) |

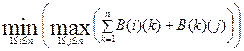
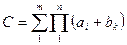
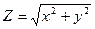 для всевозможных пар значений a и b.
для всевозможных пар значений a и b.


