
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Набережная Р. Мойки, 48, ргпуСодержание книги
Поиск на нашем сайте
*********************************************************** Воспользуйтесь функцией для печати нужного количества пробелов. 2. Напишите программу нахождения всех корней биквадратного уравнения. 3. Напишите программу вычисления P по формуле:
4. Напишите программу вычисления
5. Проверьте, делится ли заданное натуральное число на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19. 6. Вычислите max(min(3,5),min(2,6)). 7. Задача Ферма. Найдите квадрат, который в сумме со всеми его собственными делителями дает куб. 8. Вычислите (результат принадлежит Сринивазу Рамануджану).
Ответ: 3 9. Вычислите (результат принадлежит Сринивазу Рамануджану)
Ответ: 10. Вычислите (результат принадлежит Сринивазу Рамануджану)
Ответ: 11. Вычислите (результат принадлежит Сринивазу Рамануджану)
Ответ: 12. Замечательным достижением Франсуа Виеты является введение в математику задачи о нахождении бесконечного произведения. Вычислите
Разумеется, Виета не доказывает сходимости полученного бесконечного произведения, будучи интуитивно уверенным в справедливости своего предельного утверждения. Ответ: 13. По вещественному x вычислите значение функции sh(x)· tg(x+1)-tg2(2+sh(x-1)) 14. Опишите функцию Stepen(x,n), зависящую от вещественного x и натурального n и вычисляющую (посредством умножения) величину xn, и используйте её для вычисления значения выражения 2.7k+(a+1)-5. 15. Даны три натуральных числа. Определите их наибольший общий делитель. 16. Даны отрезки a, b, c и d. Для каждой тройки этих отрезков, из которых можно построить треугольник, найдите площадь данного треугольника. Определите процедуру Plo(x,y,z), определяющую площадь треугольника со сторонами x, y и z, если такой треугольник существует. 17. Опишите процедуру Socr(a,b,p,q), зависящую от целых параметров (b≠0), которая приводит дробь 18. Пусть процедура Socr(a,b,p,q), зависящая от целых параметров (b-0), приводит дробь
19. Пусть процедура MaxMin(x,y) присваивает параметру x большее из вещественных чисел x и y, а параметру y - меньшее. Опишите данную процедуру и используйте её для перераспределения значений вещественных переменных a, b и c так, чтобы выполнилось a≥b≥c. 20. Даны длины a, b и c сторон треугольника. Найдите медианы треугольника, сторонами которого являются медианы исходного треугольника. Указание. Длина медианы, проведённой к стороне a, равна
21. Опишите функцию F(m,n)=n!m!/(n+m)!, где n и m - неотрицательные целые числа. 22. Даны координаты вершин двух треугольников. Определите, какой из них имеет большую площадь. 23. Даны координаты вершин треугольника и координаты некоторой точки внутри него. Найдите расстояние от данной точки до ближайшей стороны треугольника. (При определении расстояний учесть, что площадь треугольника вычисляется и через три его стороны, и через основание и высоту.) 24. Три прямые на плоскости заданы уравнениями akx+bky=ck, k=1,2,3. Если эти прямые попарно пересекаются и образуют треугольник, то найдите его площадь. 25. Найдите наименьшее общее кратное четырех заданных натуральных чисел. 26. Два простых числа называются близнецами, если они отличаются друг от друга на 2 (таковы, например, числа 41 и 43). Найдите все пары чисел-близнецов из отрезка [n,2n], где n - заданное натуральное число, большее двух, с помощью функции распознавания простых чисел. Приведём несколько примеров чисел-близнецов: (5,7), (11,13), (17,19), (22271,22273). 27. Два натуральных числа называются дружественными числами, если каждое из них равно сумме всех делителей другого, за исключением его самого (таковы, например, числа 220 и 284, известные ещё Пифагору). Найдите все пары "дружественных" чисел, не превосходящих заданного натурального числа. Приведём ещё несколько примеров дружественных чисел: 1184 и 1210 (Н.Паганини), 17296 и 18416 (П.Ферма), 9363584 и 9437056 (Р.Декарт). 28. Задача Ферма. Найдите куб, который в сумме со всеми его собственными делителями дает квадрат. 29. Дано чётное число n>2. Проверьте для этого числа гипотезу Гольдбаха. Эта гипотеза (по сегодняшний день не опровергнутая и полностью не доказанная) заключается в том, что каждое чётное n, большее двух, представляется в виде суммы двух простых чисел. Воспользуйтесь функцией распознавания простых чисел.
30. Дано натуральное число n. Выясните, является ли оно квадратом. Определите функцию, позволяющую распознавать квадраты. 31. Даны натуральное число n. Выясните, является ли оно степенью пятерки. Определите функцию, позволяющую распознавать степени пятерки. 32. Дано натуральное число n. Выясните, является ли оно простым. Определите функцию, позволяющую распознавать простые числа. 33. Даны три натуральных числа. Определите их наибольший общий делитель. 34. Числа Фибоначчи u0,u1,u2,... определяются следующим образом: u0=1, u1=2, un=un-1+un-2 (n=2,3,...). Напишите функцию, вычисляющую un для данного неотрицательного целого n. 35. В XX в. математики обобщили понятие "дружественные числа" и занялись поиском общительных чисел - замкнутых циклов из трёх и более чисел. Например, в тройке чисел (1945330728960, 2324196638720, 2615631953920) делители первого числа в сумме дают второе число, делители второго в сумме дают третье число, а делители третьего числа в сумме дают первое число. Самый длинный из известных циклов [Сингх,2000,с.68] состоит из 28 общительных чисел, первое из которых равно 14316. Напишите функцию, устанавливающую, являются ли три заданные натуральные числа общительными числами. ЛАБОРАТОРНАЯ РАБОТА 5. 5.1 ЦЕЛЬ РАБОТЫ Познакомиться с понятиями "рекурсия", закрепить практические навыки работы с VBScript на примере реализации алгоритмов при помощи рекурсивных процедур и функций. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Рекурсия (самоповторение) – это действие, возвращающееся к “самому себе”. Существует два вида рекурсии: 1. прямая рекурсия (процедура или функция вызывает саму себя); 2. косвенная рекурсия означает, что одна процедура или функция вызывает другую процедуру или функцию, а это в свою очередь прямо или косвенно приводит к вызову первоначальной процедуры или функции. Рекурсию следует использовать только тогда, когда задача легко поддается рекурсивному решению. Важно отметить, что любая задача, которая решена рекурсивно, может быть решена и без рекурсии. С понятием "рекурсия" тесно связано понятие "рекуррентная последовательность”, вычисление n-го члена которой производится с помощью рекурсии. Определим это понятие. Числовая последовательность {хk} называется рекуррентной последовательностью, если
где k=p, p=1, …
ДЕМОНСТРАЦИОННЫЕ ПРИМЕРЫ Пример 1 'Имя файла Factorial.vbs 'Задача: вычислить значение факториала введённого натурального числа n '-------------------------------------- FUNCTION RecFact(n) 'Рекурсивное вычисление факториала If n=0 Then RecFact=1 Else RecFact=n*RecFact(n-1) End If End FUNCTION '--------------------------------------- FUNCTION NonRecFact(n) 'Вычисление факториала при помощи цикла dim P P=1 While (n>1) P=n*P n=n-1 WEnd NonRecFact=P End FUNCTION '--------------------------------------- Dim n n=CInt(InputBox("Введите натуральное число", "Вычисление факториала натурального_ n:","0")) number=n MsgBox "Рекурсивно вычисленный факториал: "&RecFact(n)&_ VbCrLf&_ "Нерекурсивно вычисленный факториал: "&NonRecFact(n)_ ,vbInformation,"Результат вычисления факториала числа "&number&":" Пример 2 'Имя файла Nod.vbs 'Задача: найти наибольший общий делитель (НОД) двух целых чисел '-------------------------------------- FUNCTION RecNod(n,m)
'Рекурсивное вычисление НОД If n=m Then RecNod=n ElseIf n>m Then RecNod=RecNod(n-m, m) Else RecNod=RecNod(n, m-n) End If End FUNCTION '--------------------------------------- FUNCTION NonRecNod(n,m) 'Вычисление НОД с помощью цикла While (n<>m) If n>m Then n=n-m Else m=m-n End If WEnd NonRecNod=n End FUNCTION '--------------------------------------- Dim n, m
n=CLng(InputBox("Введите натуральное число n", "Вычисление НОД: ","25")) m=CLng(InputBox("Введите натуральное число m", "Вычисление НОД: ","50")) MsgBox "Рекурсивно вычисленный НОД: "&CStr(RecNod(abs(n),abs(m)))&_ VbCrLf&_ "Нерекурсивно вычисленный НОД: "&CStr(NonRecNod(abs(n),abs(m)))_ ,vbInformation,"Результат вычисления НОД:" Пример 3 'Имя файла: Fib.vbs 'Задача: При помощи рекурсивной функции найти и вывести на экран ' к-й элемент последовательности Фибоначчи. Последовательность Фибоначчи: ' 1, 1, 2, 3, 5, 8, 13,... Нумерация данных чисел начинается с 0. '----------------------------------------- FUNCTION Fib(k) If k=0 or k=1 Then Fib=1 Else Fib=fib(k-1)+Fib(k-2) End If End FUNCTION '----------------------------------------- dim k k=Cint(InputBox("Введите k: ", "Вычисление к-го элемента посл-ти Фибоначчи: ")) MsgBox k&"-й"&" элемент последовательности фибоначчи: "&vbCrlf& Fib(k),_ vbInformation, "Результат: " Пример 4 'Имя файла Koren.vbs 'Задача:'Вычислить, используя рекурсию: sqr(1+(n+1)*sgr(1+(n+2)*sqr(1+(n+3)*sqr(1+... ' где n - натуральное число, ' k - количество корней '-------------------------------------- FUNCTION Kor(i, n) If i=k Then Kor=sqr(1+(n+k)) Else Kor=sqr(1+(n+i)*Kor(i+1,n)) End If End FUNCTION '--------------------------------------- Dim n,k,i n=CInt(InputBox("Введите натуральное число n: ", "Ввод параметров:","1")) k=CInt(InputBox("Введите количество корней k: ", "Ввод параметров:","1")) i=1 MsgBox "Значение вычисленного корня: "&CStr(Kor(i,n)), vbInformation, "Результат: " ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Дано натуральное число n. Вычислите (2n)! и 2n!; при этом используйте рекурсивную функцию вычисления факториала. 2. Переделайте программу Fib.vbs, так чтобы она находила к-й член последовательности Фибоначчи, но последовательность начиналась бы не с 1, а с 0: 0, 1, 1, 2, 3, 5, 8, 13, 21,... 3. Проверьте, будет ли к-й член последовательности Фибоначчи делиться на 5. 4. Опишите рекурсивную функцию Stepen(x,n), формальными параметрами которой являются вещественная переменная x и натуральная переменная n, вычисляющую величину xn следующим образом:
5. Напишите рекурсивную процедуру, при выполнении которой на экран будет выводиться отрезок натурального ряда чисел. 6. Напишите программу вычисления первого числа Фибоначчи, большего m (m>1), включающую рекурсивную функцию, которая основана на непосредственном использовании соотношения un=un-1+un-2.
7. Числа Фибоначчи второго порядка u0, u1, u2,... определяются следующим образом:
Напишите программу вычисления un для данного неотрицательного целого n. Используйте рекурсивную функцию. 8. Вычислите, используя рекурсию:
9. Опишите семантику приведённой ниже программы: Function koren(i) If i=0 Then koren=sqr(11) Else koren=sqr(11-2*sqr(11+2*sqr(11-2*koren(i-1)))) End If End Function Dim n,k,i i=CInt(InputBox("Введите количество рекурсий", "Ввод параметров","1")) msgbox "Результат: "&koren(i) ЛАБОРАТОРНАЯ РАБОТА 6. 6.1 ЦЕЛЬ РАБОТЫ Познакомиться с понятиями "массивы", закрепить практические навыки работы с одномерными и многомерными массивами ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Массив - это упорядоченный набор элементов. Массивы можно создавать из элементов любого типа (в отличие от многих других императивных языков программирования), и они могут иметь одно или несколько измерений. Одномерный массив принято называть вектором, а двухмерный - матрицей. Одномерный массив - это последовательность элементов любых типов. Каждому элементу массива соответствует индекс - целое неотрицательное число, определяющее его номер в последовательности. Первому элементу массива соответствует индекс 0. Во многих языках программирования элементы массива размещаются в памяти последовательно (другими словами, друг за другом).
Таблица 10 – Одномерный массив
Данные, хранящиеся в таблице 10 олицетворяют собой одномерный массив, состоящий из 8-ми элементов. Объявление одномерного массива имеет вид: Dim NameArray1 (N) где: 1) Dim - служебное слово (объявление переменной); 2) NameArray1 - имя переменной массива; 3) N – индекс последнего элемента в данном массиве Зная все элементы одномерного массива, то его можно объявить и другим образом: NameArray2=Array (Num1, Num2,…, NumN) где: 1) NameArray2 - имя массива; 2) Array – название функции языка VBS; 3) Num1 – 0-й элемент одномерного массива Num2 – 1-й элемент одномерного массива … NumN – N-й элемент одномерного массива Для доступа к данным, хранящимся в определённом элементе одномерного массива, следует указать имя массива и индекс элемента массива. Индекс всегда заключается в круглые скобки. Например, если вектор имеет имя Arr, то следующий оператор присваивает переменной x значение i-го элемента вектора Arr: x=Arr(i), где i – индекс нужного элемента одномерного массива Arr Пример: Задача: расположить в памяти компьютера одномерный массив, состоящий из 7-ми элементов, каждый из которых соответствует соответственно дню недели: “Понедельник”, “Вторник”, “Среда”, “Четверг”, “Пятница”, “Суббота”, “Воскресенье” Программа:
Замечание: Нумерация элементов в массиве (не только одномерном, но и в многомерном) начинается с 0, поэтому не стоит забывать, что i-тый элемент массива на самом деле по счёту является (i+1)-ым.
Примечание: Для получения имен дней недели лучше использовать функцию WeekDayName(i), которая возвращает название дня недели в соответствии с целочисленным параметром i. См. пример: 1Weekdays.vbs. Например: WeekDayName(1)= Воскресенье Перебор элементов массива Для перебора всех элементов массива (коллекции), например при выводе на экран, очень полезен специальный тип цикл: For each VarName in ArrName … Next где: ArrName – массив для перебора VarName – некоторая переменная, куда будут попадать по очереди элементы массива ArrName Например: (печать всех элементов массива на экран) For each incl in Arr1 Msgbox incl Next Одномерные массивы хорошо подходят для представления простых списков данных. Однако часто бывает необходимо представить таблицы данных в программах с организацией данных в формате строк и столбцов, подобно ячейкам в таблицах. Для этого существуют двумерные массивы или матрицы. Двухмерный массив можно представить как таблицу: Таблица 11– Двухмерный массив
Размерность матрицы – <это количество строк> на <количество столбцов> матрицы. В данном примере размерность матрицы 4 на 5. Если размерность матрицы N на N, то такая матрица называется квадратной. Главная диагональ квадратной матрицы – последовательность элементов, находящихся на воображаемой линии, соединяющей левый верхний и правый нижний углы квадратной матрицы. Побочная диагональ квадратной матрицы – последовательность элементов, находящихся на воображаемой линии, соединяющей правый верхний и левый нижний углы квадратной матрицы. Объявление двумерного массива имеет вид: Dim NameArray1 (N, M) где: 1) Dim - служебное слово; 2) NameArray1 - имя массива; 3) N, M - индексы последнего элемента в данном массиве Для доступа к данным, хранящимся в определённом элементе двумерного массива, следует указать имя массива с последующими числами, называемыми индексами элемента. Местоположение каждого элемента в матрице характеризуется двумя индексами. Первый индекс обозначает номер строки, в которой находится элемент, второй – номер столбца. Нумерация начинается с нуля. Индекс всегда заключается в круглые скобки. Например, если матрица имеет имя Mat1, то следующий оператор присваивает переменной x значение i-го элемента матрицы Mat1: x= Mat1(i,j), где i, j – индексы нужного элемента двумерного массива Mat1 Пусть данные, хранящиеся в Таблице 1, символизируют матрицу Mat1. Тогда элемент матрицы Mat1(2,3) равен числу 11. Пример: Задача: Расположить в памяти компьютера двухмерный массив:
Программа: Dim A (3, 4) A(0,0)= 1: A(0,1)= 1: A(0,2)= 1: A(0,3)= 1: A(0,4)= 1 A(1,0)= 1: A(1,1)= 1: A(1,2)= 1: A(1,3)= 1: A(1,4)= 1 A(2,0)= 1: A(2,1)= 1: A(2,2)= 1: A(2,3)= 1: A(2,4)= 1 A(3,0)= 1: A(3,1)= 1: A(3,2)= 1: A(3,3)= 1: A(3,4)= 1 В VBScript можно работать не только с одномерными и двумерными, но и n-мерными массивами (n<60). Какова величина n, столько индексов и используется для определения местоположения элемента в массиве. Работа с массивами, имеющими 4 или более измерений, быстро становится запутанной. Но чаще всего в программировании используют одно-, двух- и трёхмерные массивы. До настоящего времени мы рассматривали массивы, элементы которых имели числовые или строковые значения. Но на самом деле, элементами массивов могут быть и данные любых других типов, в том числе и массивов. Рассмотрим массив Mas2: Данный массив, безусловно, является двумерным или (другое название) матрицей. Однако мы его также можем себе представить в качестве массива массивов, а именно: одномерного массива, каждым элементом которого является одномерный массив. Объявление массива массивов Mas2 производится следующим образом:
dim Mas2 (2) ‘ объявление одномерного массива ‘ 0-му элементу одномерного массива присваивается одномерный массив, состоящий из ‘ элементов: 1, 2, 3, 4 Mas2 (0)=Array(1, 2, 3, 4) ‘ 1-му элементу одномерного массива присваивается одномерный массив, состоящий из ‘ элементов: 5, 6, 7, 8
Mas2 (1)=Array(5, 6, 7, 8) ‘ 2-му элементу одномерного массива присваивается одномерный массив, состоящий из ‘ элементов: 9, 10, 11, 12 Mas2 (2)=Array(9, 10, 11, 12)
Пусть дан трёхмерный массив Mas3 (2, 2, 3), заполненный единицами. Данный массив мы также можем представить как массив массивов: dim Mas3 (2, 2, 3) Mas2 (0)=Array (Array(1, 1, 1, 1), Array(1, 1, 1, 1), Array(1, 1, 1, 1)) Mas2 (1)=Array (Array(1, 1, 1, 1), Array(1, 1, 1, 1), Array(1, 1, 1, 1)) Mas2 (2)=Array (Array(1, 1, 1, 1), Array(1, 1, 1, 1), Array(1, 1, 1, 1)) Точно так же любой многомерный массив мы можем представить как массив массивов. Для доступа к данным, хранящимся в определённом элементе массива массивов, следует указать имя массива с последующими числами, называемыми индексами элемента, причём каждый индекс должен быть в круглых скобках: x=Mas4 (2)(3) До настоящего времени, все многомерные массивы, рассмотренные нами, имели одинаковое число элементов в каждой строке и одинаковое количество элементов в каждом столбце. То есть (если говорить о двумерных или трехмерных массивах) все матрицы имели прямоугольный вид, а трёхмерные массивы напоминали параллелепипед. Однако следует упомянуть о том, что существуют и “неровные” (нерегулярные) массивы. Нерегулярная матрица имеет, например, следующий вид: 2 3 4 5 6 7 8 9 10 Использование нерегулярных многомерных массивов не рекомендуется, однако иногда они бывают весьма полезны. Например, если нужно обработать очень большой двухмерный массив, который редко заполнен (то есть в котором многие элементы содержат нулевые значения), то нерегулярный массив мог бы быть подходящим решением проблемы. Объявлять нерегулярную матрицу удобно с использованием массива массивов. Объявим вышеописанную нерегулярную матрицу: Dim NeRegMat (3) NeRegMat (0)=Array (1) NeRegMat (1)=Array (2, 3) NeRegMat (2)=Array (4, 5, 6) NeRegMat (3)=Array (7, 8, 9, 10) Не всегда разработчику программ заранее известен размер массива. В одних случаях это зависит от информации, вводимой пользователем в диалоге, в других - от количества записей в одной из многих разновидностей файлов, в третьих - от результатов некоторых вычислений и т.д. Так или иначе, это довольно частое явление. В VBScript имеется возможность работать с массивами, размеры которых не фиксированы объявлением. Такие массивы называют динамическими или массивами переменной размерности. Динамические массивы получили свое название, потому что можно изменять число элементов в массиве при выполнении программы. Динамический массив (в сочетании с «правильным» программированием) может увеличиваться или сжиматься (уменьшаться в размере), чтобы вмещать точно необходимое число элементов без напрасного расходования памяти. Для изменения размера динамического массива используйте оператор ReDim, описываемый далее. Объявление динамического массива имеет следующий вид: Dim DynArray1 где 1) Dim – служебное слово 2) DynArray – имя переменной массива То есть, массивом может стать любая объявленная переменная Далее в программе, где это необходимо, с помощью оператора ReDim указывают размерность массива. Например: ReDim DynArray1 (5) ‘ для вектора или ReDim DynArray1 (3, 4) ‘ для матрицы или ReDim DynArray1 (2, 4, 7) ‘ трёхмерного массива При каждом выполнении оператора ReDim значения всех элементов массива, сохранённые ранее, теряются. VBScript переустанавливает их в Empty (пустое значение) (для Variant-массивов), в нулевые значения (для числовых массивов), в строки нулевой длины (для строковых массивов). Конечно, это, скорее всего, неудобно. Если вам нужно добавить к массиву новый элемент в конец массива, то есть увеличить размер массива, то нет смысла терять при этом, может быть, «с трудом полученные» ранее элементы. “К счастью”, с помощью ключевого слова Preserve в операторе ReDim можно указать, чтобы система сохранила значения массива, размеры которого изменяются. В следующем примере размер вектора увеличивается на единицу от текущего размера с сохранением значений, ранее запомненных в массиве. Текущий размер массива определяется с помощью функции UBound (подробнее о ней будет рассказано ниже): ReDim Preserve DynArray2 (UBound(DynArray)+1) VBScript имеет функцию, которая освобождают пользователя от необходимости вручную отслеживать верхний предел массива – функция UBound. Эта функция возвращают верхнее граничное значение индекса массива. Пример использования: Dim A (3, 4) ‘ объявление матрицы А MsgBox UBound (A, 1) ‘ вывод на экран максимального индекса в строке MsgBox UBound (A, 2) ‘ вывод на экран максимального индекса в столбце Ценное замечание Для того чтобы определить является ли переменная массивом можно использовать функцию IsArray(ArrName), возвращающую «Истина», тогда и только тогда когда ArrName – массив. ДЕМОНСТРАЦИОННЫЕ ПРИМЕРЫ Пример 1 'Имя файла Input_Output_1.vbs 'Программа содержит процедуру ввода и процедуру вывода одномерного массива (вектора)
Option Explicit Dim A(4) ' объявление одномерного массива А Const k=4 ' k-индекс последнего элемента в векторе '------------------------------------------------------------------------------- Sub Input (A) ' процедура ввода элементов вектора с клавиатуры ' процедура с параметрами ' A-параметр, передаваемый по ссылке ' k-глобальная константа Dim i ' параметр цикла For i=0 to k A(i)=CDbl(InputBox("Введите "&i&"-й элемент одномерного массива","Ввод “&_ “вектора A:",5)) Next End Sub '------------------------------------------------------------------------------- Sub Output (A) ' процедура вывода на экран элементов вектора ' процедура с параметрами ' A-параметр, передаваемый по ссылке ' k-глобальная константа Dim i ' параметр цикла Dim s ' строковая переменная, в которой будет сохранён массив For i=0 to k s=s+CStr(A(i))+" " Next MsgBox "Вы ввели одномерный массив:"&vbCrLf&_ s,_ vbExclamation,_ "Вывод вектора A:" End Sub '------------------------------------------------------------------------------- Input A ' вызов процедуры ввода элементов массива Output A ' вызов процедуры вывода элементов массива Пример 2 'Имя файла Input_Output_2.vbs 'Программа содержит процедуру ввода и процедуру вывода двумерного массива (матрицы) Option Explicit Dim A(4, 5) ' объявление двумерного массива А Const m=4 ' m, n -индексы последнего элемента матрицы Const n=5 '------------------------------------------------------------------------------- Sub Input (A) ' процедура ввода элементов матрицы с клавиатуры ' процедура с параметрами ' A-параметр, передаваемый по ссылке ' m, n -глобальные константы Dim i, j For i=0 to m For j=0 to n A(i,j)=CDbl(InputBox("Введите элемент A("&i&","&j&")","Ввод матрицы A:",5)) Next Next End Sub '------------------------------------------------------------------------------- Sub Output (A) ' процедура вывода на экран элементов матрицы ' процедура с параметрами ' A-параметр, передаваемый по ссылке ' m, n -глобальные константы Dim i, j Dim s ' строковая переменная, в которой будет сохранён массив For i=0 to m For j=0 to n s=s+CStr(A(i,j))+" " Next s=s&vbCrLf Next MsgBox "Вы ввели двухмерный массив:"&vbCrLf&_ s,_ vbExclamation,_ "Вывод матрицы A:" End Sub '------------------------------------------------------------------------------- Input A ' вызов процедуры ввода элементов массива Output A ' вызов процедуры вывода элементов массива Пример 3 ' Имя файла Min_Max.vbs ' Программа находит минимальный и максимальный элемент вектора Option Explicit Dim s, i Dim A(4) ' объявление одномерного массива А Const k=4 ' k-индекс последнего элемента в векторе '------------------------------------------------------------------------------- Sub Input_Rnd (A) ' процедура заполнения одномерного массива целыми ' числами от 0 до 20, выбранными случайным образом Dim i For i=0 to k Randomize A(i)=Fix(Rnd(1)*20) Next End Sub '------------------------------------------------------------------------------- Function Min (A) Dim i Min=A(0) For i=1 to k If A(i)<Min Then Min=A(i) End If Next End Function '------------------------------------------------------------------------------- Function Max (A) Dim i Max=A(0) For i=1 to k If A(i)>Max Then Max=A(i) End If Next End Function '------------------------------------------------------------------------------- Input_Rnd A ' вызов процедуры ввода элементов массива ' Вывод введённого вектора: For i=0 to k s=s+CStr(A(i))+" " Next MsgBox "Вектор, полученный случайным образом:"&vbCrLf&_ s&vbCrLf&_ "Минимальный элемент данного вектора: "&Min (A)&vbCrLf&_ "Максимальный элемент данного вектора: "&Max (A)&vbCrLf,_ vbExclamation,_ "Результат:" Пример 4 'Имя файла Simple_Nombers.vbs 'Программа находит все простые числа в двумерном массиве (в матрице) Option Explicit Dim k, i, j, p, s Dim A(4, 5) ' объявление двумерного массива А Const m=4 ' m, n -индексы последнего элемента матрицы Const n=5 '------------------------------------------------------------------------------- Sub Input (A) ' Процедура ввода элементов матрицы с клавиатуры ' процедура с параметрами ' A-параметр, передаваемый по ссылке ' m, n -глобальные константы For i=0 to m For j=0 to n A(i,j)=CDbl(InputBox("Введите элемент A("&i&","&j&")","Ввод матрицы A:",5)) Next Next End Sub '------------------------------------------------------------------------------- Function Simple (k) ' Функция возвращает True, если число k окажется простым, и false - в противном случае Dim x Simple=True If k<>1 Then For x=2 to Int(sqr(k)) If k mod x =0 Then Simple=False End If Next Else Simple=False End If End Function '------------------------------------------------------------------------------- Input A ' Вызов процедуры ввода элементов матрицы ' В цикле происходит проверка, является ли элемент матрицы простым числом For i=0 to m For j=0 to n If Simple(A(i,j)) Then ' Вызов процедуры, которая проверяет, является ли A(i,j) ' простым числом p=p&A(i,j)&" " ' если да, то число записывается в строку p End If Next Next ' Выводим введённую матрицу и те элементы массива, которые являются простыми числами For i=0 to m For j=0 to n s=s+CStr(A(i,j))+" " Next s=s&vbCrLf Next MsgBox "Вы ввели двухмерный массив:"&vbCrLf&_ s&vbCrLf&_ "Элементы массива, которые являются простыми числами: "&vbCrLf&_ p,_ vbExclamation,_ "Результат:" Пример 5 'Имя файла Zero.vbs 'Программа определяет количество нулевых элементов двумерного массива (матрицы) Option Explicit Dim k, i, j, s Dim A(4, 5) ' объявление двумерного массива А Const m=4 ' m, n -индексы последнего элемента матрицы Const n=5 Вводим матрицу k=0 For i=0 to m For j=0 to n A(i,j)=CDbl(InputBox("Введите элемент A("&i&","&j&")","Ввод матрицы A:",5)) If A(i,j)=0 Then ' проверяем, нулевой ли элемент мы ввели k=k+1 ' счётчик нулевых элементов End If Next Next ' Выводим введённую матрицу и количество нулевых элементов For i=0 to m For j=0 to n s=s+CStr(A(i,j))+" " Next s=s&vbCrLf Next MsgBox "Вы ввели двухмерный массив:"&vbCrLf&_ s&vbCrLf&_ "Количество нулевых элементов в данной матрице: "&k,_ vbExclamation,_ "Результат:" Пример 6 ' Имя файла Difference.vbs ' Программа находит разность между произведением и суммой элементов целочисленного ' одномерного массива, состоящего из 5-ти положительных элементов Option Explicit Dim i, s Dim A(4) ' объявление одномерного массива А Const k=4 ' k-индекс последнего элемента в векторе '------------------------------------------------------------------------------- Sub Input_Rnd (A) ' процедура заполнения одномерного массива целыми ' числами от 0 до 20, выбранными случайным образом Dim i For i=0 to k Randomize A(i)=Fix(Rnd(1)*20) Next End Sub '------------------------------------------------------------------------------- Function Summa (A) Dim i, s For i=0 to k s=s+A(i) Next Summa=s End Function '------------------------------------------------------------------------------- Function Multiplication (A) Dim i, s s=1 For i=0 to k s=s*A(i) Next Multiplication=s End Function '------------------------------------------------------------------------------- Function Difference (multiplication, summa) Difference=multiplication-summa End Function '------------------------------------------------------------------------------- Input_Rnd A ' вызов процедуры ввода элементов массива ' Вывод введённого вектора: For i=0 to k s=s+CStr(A(i))+" " Next MsgBox "Вектор, полученный случайным образом:"&vbCrLf&_ s&vbCrLf&_ "Произведение элементов вектора: "&Multiplication (A)&vbCrLf&_ "Сумма элементов вектора: "&Summa (A)&vbCrLf&_ "Разность между произведением и суммой элементов данного”&_ “вектора:"&vbcrLf&_ Difference(multiplication (A), summa (A)),_ vbExclamation,_ "Результат:" Пример 7 ' Имя файла Array of Arrays.vbs ' Дана нерегулярная матрица: 1 3 -4 ' -2 5 5 7 ' 6 3 -6 ' 5 5 7 2 -8 ' Задача: Найти в данной матрице все отрицательные элементы и распечатать их вместе с 'индексами. Option Explicit ' Объявление матрицы как массива массивов Dim Arr(3) Arr(0)=Array(1, 3, -4) Arr(1)=Array(-2, 5, 5, 7) Arr(2)=Array(6, 3, -6) Arr(3)=Array(5, 5, 7, 2, -8) dim i, j, s ' В данном цикле организована проверка каждого элемента матрицы, является ли ' он отрицательным. если да, то данный элемент вместе со своими индексами сохраняется ' в строку s For i=0 to 3 For j=0 to UBound(Arr(i)) ' Функция UBound возвращает индекс последнего элемента ' в i-той строке If Arr(i)(j)<0 Then s=s&"A("&i&", "&j&") = "&Arr(i)(j)&vbCrLf End if Next Next ' Вывод исходной матрицы, а также найденных в ней отрицательных элементов, вместе ' с их индексами MsgBox "Дана матрица A:"&vbCrLf&_ " 1 3 -4"&vbCrLf&_ "-2 5 5 7"&vbCrLf&_ " 6 3 -6"&vbCrLf&_ " 5 5 7 2 -8"&vbCrLf&_ "Отрицательные элементы данной матрицы:"&vbCrLf&_ s,_ vbExclamation, "Результат:" Пример 8 ' Имя файла Dynamic_Array.vbs ' Дана матрица A размерностью 4 на 3 и вектор B, состоящий из 4-х элементов. ' Сформировать новую матрицу A размерностью 4 на 4, которая бы содержала в себе ' матрицу A и вектор B, в качестве последнего столбца.
Option Explicit Dim i, j Dim B(3) ' объявление вектора B, состоящего из 4-х элементов Dim A() ' объявление динамического массива А '------------------------------------------------------------------------------- Sub Input_Rnd_Arr (A) ' процедура заполнения двумерного массива целыми ' числами от 0 до 20, выбранными случайным образом ReDim A (3, 2) For i=0 to 3 For j=1 to 2 Randomize A(i,j)=Fix(Rnd(1)*20) Next Next End Sub '------------------------------------------------------------------------------- Sub Input_Rnd_Vec (B) ' процедура заполнения одномерного массива целыми ' числами от 0 до 20, выбранными случайным образом For i=0 to 3 Randomize B(i)=Fix(Rnd(1)*20) Next End Sub '------------------------------------------------------------------------------- Function Arr_to_Str (A) ' функция записи матрицы в строку s Dim s For i=0 to 3 For j=1 to 2 s=s&A(i,j)&" " Next s=s&vbCrLf Next Arr_to_Str=s End Function '------------------------------------------------------------------------------- Function Vec_to_Str (B) Dim s ' функция записи вектора в строку s For i=0 to 3 s=s&B(i)&" " Next Vec_to_Str=s End Function '------------------------------------------------------------------------------- Function New_Arr(A, B) Dim s ' функция формирования новой матрицы A и запись её в строку s ReDim Preserve A (3, 3) A(0, 3)=B(0) A(1, 3)=B(1) A(2, 3)=B(2) A(3, 3)=B(3) For i=0 to 3 For j=1 to 3 s=s&A(i,j)&" " Next s=s&vbCrLf Next
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.188.114 (0.018 с.) |



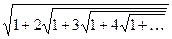
 , где знаки перед корнями периодически повторяются группами по три:"-", "+", "-".
, где знаки перед корнями периодически повторяются группами по три:"-", "+", "-".
 где знаки перед корнями периодически повторяются группами по три:"-", "+", "-".
где знаки перед корнями периодически повторяются группами по три:"-", "+", "-".
 где знаки перед корнями периодически повторяются группами по три: "-", "+", "+".
где знаки перед корнями периодически повторяются группами по три: "-", "+", "+".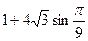


 к несократимому виду
к несократимому виду  .
. .
.







