
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет напряжений сдвига в изоляционном покрытии верхней половины трубопроводаСодержание книги
Поиск на нашем сайте Рассмотрим распределение напряжений в верхней половине трубопровода (рис 4,а) Вертикальное давление грунта в произвольно расположенной на верхней полуокружности трубопровода точке А, координата которой определена радиусом ОА, проведенным под углом β к вертикальному диаметру, равно НАγГ. Высота грунтовой засыпки над точкой А:
где Н0 - высота засыпки от верхней точки вертикального диаметра трубопровода до уровня поверхности земли. Тогда давление грунта над точкой А:
Представляя цилиндрическую поверхность трубопровода как наклонную плоскость с переменным углом наклона β, получим для нормальных и касательных напряжений:
Рис 4 Схемы к расчету напряжений в верхней половине трубопровода
Подставим в (20) и (21) значение рА из (19):
Определим точки приложения максимальных нормальных и касательных напряжений. Для этого продифференцируем уравнения (22) и (23) и приравняем нулю их первые производные. Для нормальных напряжений имеем выражение
разделив (24) на cos β sin β, получим
откуда
Как видно из выражения (26), значение угла β определяющего положение точки приложения максимальных нормальных напряжений, зависит от отношения Определим предельные значения β. При Н0 = 0 β = 48°. Представляет интерес установить, при каких условиях β =0. Для этого решаем:
Получаем Таким образом, угол β, определяющий положение точки приложения максимальных нормальных напряжений, во всех случаях не превышает 48°, а при Для касательных напряжений получаем
Заменив переменные
Решение последнего уравнения в общем виде не приводится к компактной форме, позволяющей установить зависимость угла β, определяющего положение точки приложения максимального касательного напряжения, от отношения Определим граничные значения угла β. При D = 0 (диаметр трубопровода пренебрежимо мал по сравнению с высотой засыпки):
Решение (31) дает значение β =4'5°. При Н = 0:
Решение (32) дает значение β =64°20'. Учитывая, что нормальные напряжения на опорной части трубопровода больше, чем на ее верхней половине, а касательные напряжения в изоляционном покрытии верхней половины трубопровода при оседании грунтовой засыпки в пазухах траншеи являются активными (в отличие от касательных напряжений в нижней половине), рассмотрим имеющий практическое значение расчет касательных напряжений в верхней половине изоляционного покрытия трубопровода. Для расчета воспользуемся уравнением (23), в которое вводим дополнительный член Н1,учитывающий увеличение давления на трубу от оседания грунтовой засыпки в пазухах:
Н1 определим на основании следующих посылок. При обследованиях действующих трубопроводов неоднократно замечено разрушение защитной обертки в окрестности точки, характеризуемой углом β =35...45°. Одной из возможных причин такого разрушения является осадка грунтовой засыпки в боковых пазухах траншеи. При этом грунт как бы сползает по поверхности трубы, а так как он связан с изоляционным покрытием силами трения, то в покрытии возникают нормальные напряжения растяжения, а в адгезионном слое — касательные напряжения сдвига. Очевидно, что грунт не может «сползать» с горизонтальной поверхности, а также с наклонной поверхности при небольших углах наклона р. Минимальное значение β, при котором происходит сползание грунта с наклонной поверхности или, что то же, с боковой поверхности трубопровода, будем считать характеристикой границы разлома грунта. Границей разлома грунта будем называть условную горизонтальную линию на боковой поверхности трубы, ниже которой грунт может «сползать» с поверхности трубы. Вполне обоснованным представляется предположение, что место разрыва защитной обертки соответствует положению границы разлома. Из условия статического равновесия тела на наклонной плоскости следует, что положение границы разлома соответствует значению β = φ, (34) где φ - угол внутреннего трения грунта. Дополнительную составляющую давления грунта, обусловленную оседанием грунтовой засыпки в боковых пазухах траншеи, определим, считая половину веса грунта в боковых пазухах траншеи равномерно распределенной по части диаметра, соответствующей границе разлома грунта. Тогда:
Если рекультивация земель после укладки и засыпки трубопровода не выполнялась, а вынутый грунт уложен над траншеей валиком, то высота засыпки возрастает на величину Н2, которую можно оценить следующим образом. Предположим, что сечение валика имеет площадь треугольника, основание которого равно ширине траншеи В, а площадь равна площади поперечного сечения трубы
Из рис. 4 видно:
откуда
Кроме того, величина Н1, учитывающая повышение давления грунта от оседания засыпки в боковых пазухах траншеи, также возрастает. Это увеличение обозначим ΔН1. Считая, что половина веса грунта над боковой пазухой траншеи (на рис. 4, б) этот грунт обозначен треугольником с основанием
Учитывая, что решения уравнения (30) при. D = 0,72...1,42 м и H0 =1...3 м дают значения угла, определяющего точку приложения максимальных касательных напряжений, весьма близкие к β = 45°, получаем формулу для расчета касательных напряжений:
Задания для студентов №3 Таблица 3
Задача №4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 , (18)
, (18)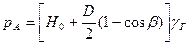 . (19)
. (19)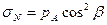 , (20)
, (20) (21)
(21) а
а
 б
б
 , (22)
, (22) . (23)
. (23) , (24)
, (24) , (25)
, (25) . (26)
. (26) .
. (27)
(27) .
. и
и  . (28)
. (28) . (29)
. (29) , приводим уравнение (29) к канонической форме кубического уравнения:
, приводим уравнение (29) к канонической форме кубического уравнения: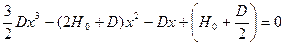 . (30)
. (30) . (31)
. (31) . (32)
. (32) . (33)
. (33) (35)
(35) (рис. 4, б). Высота этого треугольника
(рис. 4, б). Высота этого треугольника (36)
(36) (37)
(37) . (38)
. (38) и высотой h) равномерно распределена по горизонтальной проекции дуги, отсекаемой границей разлома грунта
и высотой h) равномерно распределена по горизонтальной проекции дуги, отсекаемой границей разлома грунта  , получаем для ΔН1 выражение
, получаем для ΔН1 выражение . (39)
. (39) . (40)
. (40)


