
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальные формы схем отношенийСодержание книги Поиск на нашем сайте
Нормализация отношений выполняется декомпозиций их схем. Декомпозиция схемы с атрибутами R(A1 …. An) - называется знаменной схемы совокупностью схем. Которое при выполнении операции объединения получает в результате нашу исходную функцию. При этом не требуется, чтобы схемы Ri не были пересекающими. P = {R1, R2, R3} = R1
Существует 5 уровней нормализации схем отношении: 1) НормФорма 2) НФ 3) НФ 4) НР Бойса-Кодда 5) НФ 6) НФ
Нормальные формы подчиняются правилу вложенности по возрастанию номеров. Схема отношения находится в первой нормальной форме, когда все входящие в нее атрибуты явл аддаморнными. Значения соответствующего домена явл не делимыми, а не как множество или картежей. 12.03.2015 Лекция 10 Рейсы (№ рейса, Пункт Отправления, Пункт Назначения, Расписания) R7 Харьков – Киев Пнд 8 Вт 14 Ср 10 В67 Харков – Полтава Ср 12, Сб 14
Вторая НФ Если Х – это ключ отношения R Y < X, то в отношений R имеет место частичная зависимость (нне полная функц зависимость), когда есть f: X => A Y => A Где А - не первичный атрибут отношения Если это условия не выполняется, то первичный атрибут А функционально зависит от Х Схема отношений Если схема отношений R находится во второй НФ если она находится впервой НФ и каждый ее не первичный атрибут функционально полный и зависит от ключа. Работник (ФИО, Место работы, Должность) Сидоров => Хаи => Преподаватель Петров => Хаи =>Инженер В отношении присутствует 2 семантических фактора и 2 функциональной зависимости. Чтобы удалить полную функциональную зависимость (Должность от место работы) необходимо выполнить декомпозицию отношения работы на 2 отношения. Место работы (ФИО, Организация) Сидоров Хаи Петров ХАИ Организация (Предприятия, Должность) Хаи Преподователь Хаи Инженер
Третья НФ Схема отношения R находится втретей НФ если не существует ключа Х для отношения R множества атрибутов этого отношения Y (Y <= R) и А є R F: X => Y Y => A Но нет зависимости Схема отношения R находится в третей НФ, если она находится второй НФ и каждый не первичный атрибут не транзитивно зависит от первичного ключа.
ФИО – место работы Мастера – должность
Когда отношения имеет только 1 ключ и др. зависимости в том числе многозначные в нем отсутствуют, то третья НФ освобождает от избыточности и аномалии выполнения операции. Если в отношении находящийся в третьи НФ отсутствует, но имеются др. зависимости, кроме зависимости от ключа, то в третей НФ имеется аномалия. В этом случае рассматривают усиленную третьи НФ Бойса-Кодда. НФ Бойса-Кодда Схема отношения R функциональности зависимостями f если когда в отношений R есть f: X => A A То Х является возможным ключом отношения R ДОПИСАТЬ Нормализованная схема находится в НФ Бойса-Кодда, если в каждой детерминанта является возможным ключом. Пусть у нас имеется отношения Проект (Деталь, Проект, Поставщик) Деталь, Поект – Поставщик Поставщик, Проект Отражающее использования проекта деталей поставляемого поставщика. Деталь поставляется 1 поставщиком. Поставщик обслуживает только 1 проект, но проекты обслужывабтся несколькими поставщиками.
Четвёртая НФ Если в отношений присутствует многозначные зависимости то схема должна находится в четвертой НФ. В противном случае будут возникать соответствующий аномалий с операцыями событий. Схема отношений R будет находится в четвертой НФ, если всякий раз существует многозначная зависимость У от Х и где У!= Х F: X => => Y Y!= 0 Y <= X не явл под множеством X Также сузествует зависимость функцыональнная F: X => A, то есть Х - ключ А – не клбючевой атрибут
Отношения находится вчертверотй НФ Пусть у нас имеется отношения Производство (ИНН, Дети, Дисцыплины, Должность) 1273 Александр СА доцент 1273 Ольга СА доцент 1273 Александр ИО доцент 1273 Ольга ИО доцент 1273 Сергей СА доцент 1273 Сергей ИО доцент 1273 Александр Матем проф 1273 Сергей Матем проф 1273 Ольга Матем проф
13.03.2015 Лекция 11 Пятая НФ (Проекция или соедините) Тот факт что отношение может быть восстановлено, без потерь соединения некоторых его проекции известен как зависимость по соединениям. Отношения находится в пятой НФ, тогда и только тогда когда любая зависимость по соединению в отношении определяется возможными ключами этого отношения. То есть каждая проекция содержит не менее одного ключа и по крайнем мере 1 не первичный атрибут. R (Поставщик, Деталь, Отдел) П1 Д1 О1 П1 Д2 О2 П2 Д1 О1 П2 Д3 О2 П3 Д1 О1 П3 Д2 О3
R1 R2 и R3 находятся в 5НФ, т.к. при помощи операции соединения мы получим исх форму R Отношения R отсутствует относительно многозначной зависимости и это отношения состоит из первич атрибутом то есть явл полностью ключевым, поэтому отношения находится в 4НФ. R1 and R2 и R3 находятся в 5 НФ так как удовлетворяют от зависимости по соединению этих отношений. Преимущества НФ состоит в том что исчезает избыточность, следовательно уходят аномалии обновления данных. Шестая НФ Это обобщённая 5 НФ для хронологической БД. Отношения находится 6 НФ тогда когда она удовлетворяет всем нетривиальным зависимостям соединение, то есть не может быть подвергнута дальнейшей декомпозициям без потерь.
Работник (ИНН, Время раб., Должность, Адрес Проживания) 1267 1.1.2000 – 31.12.2005 Инженер Чкалова 18 1267 1.1.2006 – 31.12.2010 научн.сотрудник Чкалова 18 1267 1.1.2011 – 31.12.2012 доцент Сумская 5 1267 1.1.2013 – 31.12.2014 доцент Сумская
Должность Проживания
Домена ключевая НФ (ДКНФ) Это Одна из возможных форм она была предложена в 1981г. Рональдом. Отношения находится в домен-ключевой НФ тогда и только тогда, когда наложено на нее ограничения является логическим следствием ограничений доменов и ограничений ключей, наложенное на данное отношение. Ограничение домена – ограничение, предписывающее использовать для определённого атрибута значения только из некоторого заданного домена. Ограничение по своей сути – задание перечня допустимых значений типа и объявлений о том что указанный атрибут имеет данный тип. Ограничения ключа - это ограничение утверждает, что указанный атрибут явл потенциальным ключом. Любое отношение находящийся в доменной ключевой НФ обязательно находится в 5НФ, однако не любое отношение можно привести доменной ключевой НФ.
Пример Заданы ограничения: Общежитие => Оплата, №к – начинается с 1 Отношения: Студент (№ зачетной книжки, курс, Общежитие, Оплата) Оплата Общ (Общежитие, Оплата) Студент (№к, Курс) № кн – СDDDDD · С – “1” · D – цифры Курс = {D} – цифры Общежитие = {String} Оплата = {DEC(4)} Общ -> Оплата № кн -> Курс, Общ. Реляционная алгебра Реляционные модели данных кроме структуры данных должны входить операции манипулирования данных. На более известными языка запроса в реляционной модели данных является реляционная алгебра и реляционная исчисление. В классическом понимание алгебра понимается как пара в которой складывается из основного множества и множества операции(сигнатура). При этом аргументы и результат каждой операции принадлежит основному множеству. Реляционная алгебра – это алгебра строгом классическом понимании ее определения. Элементами основного множества является реляционные отношения. В связи с этим операции алгебры могут вкладывается одна в одну то есть аргумента конкретной информации, может быть результат выполнения др. операции. Это дает возможность записывать запросы произвольного уровня сложности виде выражении, которые содержат вложенные одна в одну операции. Операции реляционной алгебры Сигнатура реляционной алгебры Кодда содержит из 8 операции. Введем понятия совместимости реляционных отношении. Это понятия необходимо так как некоторые операции такие как теоритико -множественные операции, объединение, пересечение, разность определенны только для совместимых отношений. Реляционное отношение R1(A1 …. Am) и реляционных отношении R2(B1 …. Bk) m=k совместимы, если: 1) У них одинаковое количество атрибутов 2) Можно установить взаимно однозначное соответствие между доменами атрибутов первого и второго отношения. То есть домены сопоставленных атрибутов должны быть одинаковые.
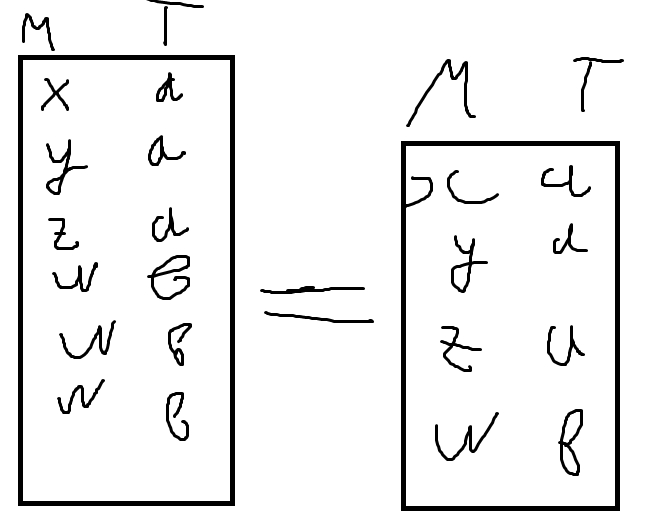
26.03.2015 Лекция 11 Отметим некоторые особенности бинарных операции: 1) Операция ϕ комуникативна, если AB = BA 2) Операция ϕ ассоциативно, если выполняется (AϕB) ϕC = Aϕ (BϕC) 3) Операция ϕ дистрибутивная по отношению Θ, если Aϕ(BΘC) = (AϕB)Θ(AϕC) Рассмотрим 5 основных операции проекции объединении, разности, декартовых произведения и селекция. Другие часто используемые операции такие как пересечение, соединение и деление можно выразить через 5 основных операции. Представим отношения которое будем использовать в примере ПРИМЕР 1: P (D1 D2 D3) 1 11 x 2 11 g 3 11 z 4 12 x Q (D4 D5) X 1 X z Y 1 S (A B) 5 a 10 b 15 c 2 d 6 a 1 b R (M P Q T) Y 101 5 a Y 105 3 a Z 500 3 a W 50 1 b W 10 2 b W 300 4 b Проекция 1 операция представляет собой выборку из каждого картежа отношении, значения атрибутов входящих в список А, которое является подмножества U(A<U). И удаления из полученных повторяющих строк(картежей) R[A] {r [A]: r є R} r – это картежная переменная значения которого является картежа исходного отношения R, а r[A] часть картежа р с атрибутами из списка [A] Пример Необходимо найти отношения R[M, T] = Операция объединение Это операция коммуникативно, ассоциативно и дистрибутивно к операции пересечения. Алгебра зап так
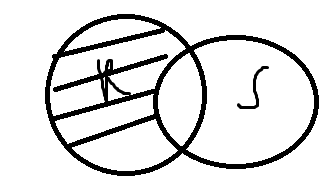
Для того чтобы объединение было возможны отношения операнды R and S должны быть совместимы по объединению. То есть их атрибуты должны быть определенны на совместимыми доменами. {t: t є R v t є S}
A B A B 5 a R[ Q T] u S = 5 a 5 a 3 a 3 a 10 b 9 a 9 a U 15 c = 1 b 1 b 2 d 2 b 2 b 6 a 4 b 4 b 1 b 10 b 15 c 2 d 6 a
Операция Разность Это операция не коммутативно не ассоциативно, не дистрибутивна к другим операциям. Алг зап так R - S отношения {t: t є R л t
Кроме этого операнды должны быть совместимы по доменам, т.е. их атрибуты должны быть определенны над совместимыми доменами. Q T A B 5 a 5 a 3 a 3 a 12 b 9 a R [Q T] – S = 9 b - 15 c = 2 b 1 b 2 d 4 b 2 b 6 a 4 b 4 b
Декартовое произведение Эта операция коммутативная и социативная с др. операциями Флгебра зап так
Конкатенация - r || S Операция осуществляется между отношениями картежав результатом является конкатенация или сцепления соответствующих картежей. G (R x S) = G(R) + Gt (S) Мощность - M(R x S) = M(R) x M(S) На практике используются ограниченный вариант этой операции которое называется соединением. Ra= R[M T] Rb = Q [D4 D5] МГ D4 D5 M T D4 D5 xa x1 X a x 1 xa x2 Rs = Ra x Rb = g a x x 2 = xa y1 Z a y 1 ya x1 W b ya x2 Ya y2 Za x1 Za x2 Za y1 Wb x1 Wb x2 Wb y1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |



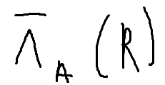
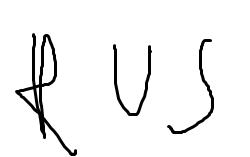 {t: t є R v t є S}
{t: t є R v t є S}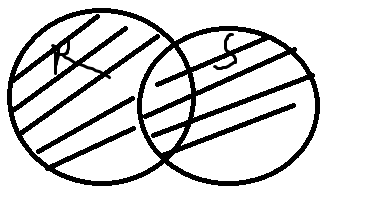
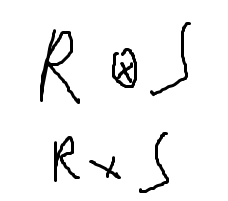 {(r || S): r є R л S
{(r || S): r є R л S


