
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Базовые финансовые функции сложного процентаСодержание книги
Поиск на нашем сайте
Обозначения в приведенных выше формулах: PV — текущая стоимость денежной единицы; i — годовая процентная ставка; n — количество лет (периодов); k — количество платежей в течение одного года (периода); FV – будущая стоимость денежной единицы; РМТ – единовременный платеж n-ого периода. Рассчитайте по условиям задач значения базовых функций сложного процента.
Цена капитала на финансовом рынке определяется процентной ставкой. Она зависит от ряда факторов, основными из которых являются спрос и предложение денежных ресурсов на финансовом рынке. Процентная ставка используется для определения стоимости денег с учетом временного фактора. Могут применяться простые, сложные и непрерывно начисляемые процентные ставки. При сравнении разновременных денежных потоков особую роль играет понятие приведенная {текущая) стоимость денежных потоков. На практике применяются шесть процентных множителей: 1.Множитель сложного процента, который выражает стоимость 1 руб., инвестированного сегодня под г % в год сроком на п лет. Будущая величина инвестированных сегодня V руб. определяется как произведение множителя сложного процента на сумму инвестиций V. 2.Множитель приведенной стоимости 1 руб. выражает сегодняшнюю стоимость 1 руб., который будет получен через n лет при процентной ставке, равной r % в год. Для определения приведенной величины 5 руб., получаемых через п лет, необходимо значение V умножить на множитель приведенной стоимости 1 руб. 3.Множитель сложного процента для аннуитета, который позволяет найти будущую стоимость вложений в виде аннуитетов в 1 руб. под r % в течение n лет. 4.Множитель приведенной стоимости 1 руб. аннуитета, который позволяет определить при заданной процентной ставке приведенную величину денежных потоков в виде аннуитетов, получаемых в течение ряда лет начиная с будущего года. 5.Множитель накопительного фонда, который позволяет определить, сколько денежных средств необходимо инвестировать каждый период под r % в период, чтобы через п периодов на счету был накоплен 1 руб. 6.Множитель погашения кредита выражает собой сумму денег, которую необходимо платить каждый период в течение п периодов с целью погашения кредита в 1 руб., полученного под r % в период. Если денежные потоки изменяются, подчиняясь закону арифметической прогрессии, приведенная величина потоков рассчитывается как сумма приведенной величины аннуитетов и приведенной величины приростной части таких денежных потоков. Если денежные потоки изменяются, подчиняясь закону геометрической прогрессии, значение приведенной величины таких потоков будет зависеть от величины ставки дисконтирования и знаменателя геометрической прогрессии. При заключении кредитного соглашения с банком заемщик должен ориентироваться на минимум издержек, связанных с обслуживанием долга, поскольку разные схемы погашения кредита обусловливают разные издержки по амортизации основного долга.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.230.221 (0.009 с.) |



 коэффициент накопления денежной единицы
коэффициент накопления денежной единицы

 - фактор фонда возмещения
- фактор фонда возмещения

 -дисконтный множитель
-дисконтный множитель

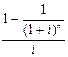 коэффициент приведения ренты
коэффициент приведения ренты

 коэффициент погашения задолженности
коэффициент погашения задолженности



